
Charakteristika metody minimálních nákladů, výhody, nevýhody

The metoda s nejnižšími náklady je postup používaný k získání počátečního proveditelného řešení problému s přepravou. Používá se, když je prioritou snížit náklady na distribuci produktu.
Metoda nejnižších nákladů usiluje o dosažení nejnižších nákladů na dopravu mezi několika středisky poptávky (destinace) a několika středisky nabídky (zdroje)..

Produkční nebo dodavatelská kapacita každého zdroje, stejně jako požadavek nebo poptávka každého cíle, jsou známé a pevné..
Rovněž jsou známy náklady na přepravu jednotky produktu z každého zdroje do každého místa určení..
Produkt musí být přepravován z různých zdrojů do různých destinací tak, aby vyhovoval poptávce každého cíle a současně minimalizoval celkové náklady na dopravu..
Lze použít i jiné metody, pokud je prioritou spíše úspora času než úspora nákladů.
Rejstřík článků
- 1 Funkce
- 1.1 Kroky metody nejnižších nákladů
- 1.2 Aplikace
- 2 Výhody
- 3 Nevýhody
- 4 Příklad
- 4.1 Vysvětlení metody
- 5 Reference
Vlastnosti
Optimální alokace produktu z různých zdrojů do různých destinací se nazývá dopravní problém..
- Přepravní modely se zabývají přepravou produktu vyrobeného v různých závodech nebo továrnách (zdroje dodávek) do různých skladů (místa určení poptávky).
- Cílem je uspokojit požadavky destinací v rámci omezení výrobní kapacity závodů při minimálních nákladech na dopravu..
Kroky metody nejnižších nákladů
Krok 1
Je vybrána buňka, která obsahuje nejnižší náklady na dopravu v celé tabulce. Této buňce je přiřazeno co nejvíce jednotek. Toto množství může být omezeno omezeními nabídky a poptávky..
V případě, že několik buněk má nejnižší náklady, bude vybrána buňka, ve které lze provést maximální alokaci.
Poté přistoupíme k úpravě nabídky a poptávky, které jsou v ovlivněném řádku a sloupci. Upravuje se odečtením částky přiřazené buňce.
Krok 2
Řádek nebo sloupec, ve kterém byla vyčerpána nabídka nebo poptávka (ať už nulová), je vyloučena.
V případě, že se obě hodnoty, nabídka i poptávka, rovnají nule, lze libovolně vyloučit jakýkoli řádek nebo sloupec.
Krok 3
Předchozí kroky se opakují s další nejnižší cenou a pokračují, dokud není uspokojena veškerá dostupná nabídka v různých zdrojích nebo veškerá poptávka z různých cílů..
Aplikace
- Minimalizujte náklady na přepravu z továren do skladů nebo ze skladů do maloobchodních prodejen.
- Určete umístění s nejnižšími náklady v nové továrně, skladu nebo prodejní kanceláři.
- Určete plán výroby s minimálními náklady, který splňuje poptávku společnosti s omezeními výroby.
Výhoda
Metoda nejnižších nákladů je považována za produkci přesnějších a optimálních výsledků ve srovnání se severozápadním rohem.
Důvodem je, že metoda severozápadního rohu zohledňuje pouze požadavek na dodávku a dostupnost, přičemž jako počáteční příspěvek je použit levý horní roh, bez ohledu na náklady na dopravu..
Na druhou stranu metoda minimálních nákladů zahrnuje náklady na dopravu během provádění úkolů..
- Na rozdíl od metody severozápadního rohu poskytuje tato metoda přesné řešení, protože při mapování zohledňuje náklady na dopravu.
- Metoda nejnižších nákladů je velmi jednoduchá metoda.
- Pomocí této metody je velmi jednoduché a snadné vypočítat optimální řešení.
- Metoda nejnižších nákladů je velmi snadno pochopitelná.
Nevýhody
- K dosažení optimálního řešení je třeba dodržovat určitá pravidla. Metoda nejnižších nákladů je však krok za krokem nenásleduje.
- Metoda nejnižších nákladů se neřídí žádnými systematickými pravidly, pokud dojde ke shodě s nejnižšími náklady.
- Metoda nejnižších nákladů umožňuje výběr prostřednictvím pozorování zaměstnanců, což by mohlo vést k nedorozuměním k získání optimálního řešení.
- Nemá schopnost poskytnout jakýkoli druh kritérií k určení, zda je řešení získané touto metodou nejoptimálnější..
- Množství nabídek a poptávek je vždy stejné, protože se časem nemění..
- Nezohledňuje jiné typy faktorů, které je třeba přiřadit, ale pouze faktor dopravních nákladů.
Příklad
Koncept metody nejnižších nákladů lze pochopit prostřednictvím následujícího problému:
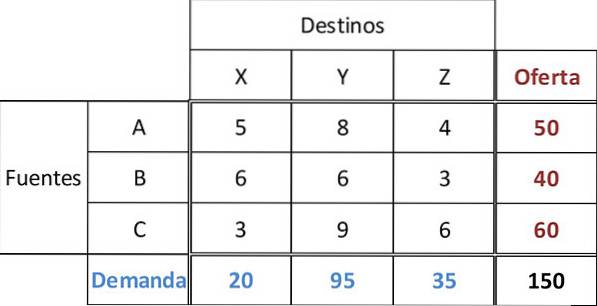
V této tabulce je napájení každého zdroje A, B, C 50, 40 a 60 jednotek. Poptávka tří maloobchodníků X, Y, Z je 20, 95 a 35 jednotek. U všech tras jsou uvedeny náklady na dopravu.
Minimální náklady na dopravu lze zjistit podle následujících kroků:
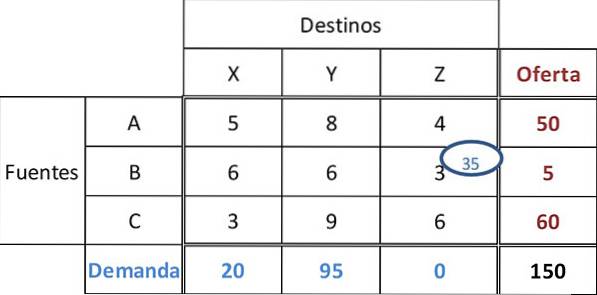
Minimální cena v tabulce je 3, s remízou v buňkách BZ a CX. Obecně platí, že pro získání nejlepšího počátečního řešení je třeba zvolit náklady tam, kde lze alokovat největší částku.
Proto bude buňce BZ přiřazeno 35 jednotek. To uspokojuje poptávku maloobchodníka Z a ponechává 5 jednotek ve zdroji B..
Vysvětlení metody
Minimální cena je opět 3. Proto bude buňce CX přiřazeno 20 jednotek. Tím je uspokojena poptávka maloobchodníka X a ve zdroji C zbývá 40 jednotek.
Další minimální cena je 4. Poptávka po Z je však již dokončena. Jdeme na další minimální cenu, která je 5. Také poptávka po X již byla dokončena.
Další minimální cena je 6 se spojením mezi třemi buňkami. Nelze však přiřadit jednotky buňkám BX a CZ, protože poptávka maloobchodníků X a Z je uspokojena. Pak je buňce BY přiřazeno 5 jednotek. Tím je dodávka zdroje B dokončena.
Další minimální cena je 8, přiřazení 50 jednotek buňce AY, dokončení dodávky ze zdroje A..
Další minimální cena je 9. Jednotce CY je přiřazeno 40 jednotek, čímž je dokončena poptávka a nabídka pro všechny destinace a zdroje. Výsledné závěrečné zadání je:
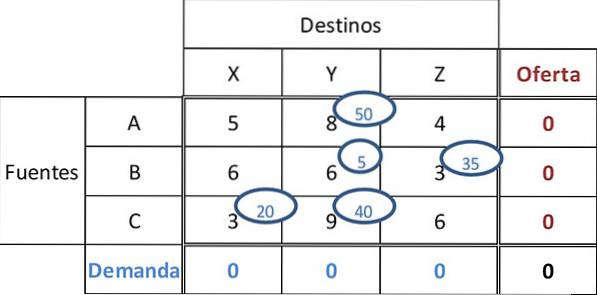
Celkové náklady lze vypočítat vynásobením přidělených částek náklady v příslušných buňkách: Celkové náklady = 50 * 8 + 5 * 6 + 35 * 3 + 20 * 3 + 40 * 9 = 955.
Reference
- Business Jargons (2019). Metoda nejmenších nákladů. Převzato z: businessjargons.com.
- Assignment Consultancy (2019). Nápověda k metodě přiřazení metody nejnižších nákladů. Převzato z: assignmentconsultancy.com.
- Řízení podniku (2015). Problém s přepravou. Převzato z: engineering-bachelors-degree.com.
- Josefina Pacheco (2019). Co je metoda nejmenších nákladů? Web a společnosti. Převzato z: webyempresas.com.
- Atozmath (2019). Příklad metody nejnižších nákladů. Převzato z: cbom.atozmath.com.



Zatím žádné komentáře