
Historické trojúhelníky, prvky, klasifikace, vlastnosti

The trojúhelníky Jsou to ploché a uzavřené geometrické obrazce, skládající se ze tří stran. Trojúhelník je určen třemi úsečkami, které protínají dvě po druhé a tvoří mezi sebou tři úhly. Trojúhelníkový tvar plný symboliky je přítomen v nesčetných objektech a jako konstrukční prvek.
Původ trojúhelníku se v historii ztratil. Z archeologických důkazů je známo, že primitivní lidstvo to dobře vědělo, protože archeologické pozůstatky potvrzují, že byl používán v nástrojích a zbraních.

Je také jasné, že staří Egypťané měli solidní znalosti geometrie a zejména trojúhelníkového tvaru. Odrážely se v architektonických prvcích jeho monumentálních budov.
V papoušku Rhind jsou vzorce pro výpočet ploch trojúhelníků a lichoběžníků, stejně jako některé objemy a další koncepty rudimentární trigonometrie.
Pokud jde o jejich část, je známo, že Babylóňané byli schopni vypočítat plochu trojúhelníku a dalších geometrických obrazců, které použili pro praktické účely, například pro rozdělení pozemků. Rovněž měli znalosti o mnoha vlastnostech trojúhelníků.
Byli to však staří Řekové, kdo systematizoval mnoho dnes převládajících geometrických konceptů, ačkoli většina těchto znalostí nebyla výlučná, protože byla jistě sdílena s ostatními starověkými civilizacemi..
Rejstřík článků
- 1 Prvky trojúhelníku
- 1.1 Zápis
- 2 typy trojúhelníků
- 2.1 Shoda trojúhelníků
- 2.2 Podobnost trojúhelníků
- 3 Vlastnosti
- 4 věty
- 4.1 Thalesova první věta
- 4.2 Thalesova druhá věta
- 4.3 Pytagorova věta
- 5 Plocha trojúhelníku
- 6 Příklady trojúhelníků
- 6.1 Příklad 1
- 6.2 Příklad 2
- 6.3 Příklad 3
- 7 cvičení
- 7.1 Cvičení 1
- 7.2 Cvičení 2
- 8 Reference
Trojúhelníkové prvky
Na následujícím obrázku jsou uvedeny prvky libovolného trojúhelníku. Existují tři: vrcholy, strany a úhly.
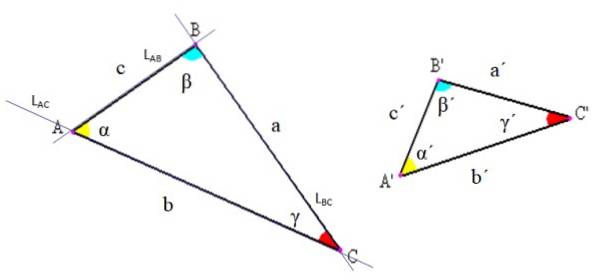
-Vrcholy: jsou průsečíky přímek, jejichž segmenty určují trojúhelník. Na obrázku výše je to například řádek LAC obsahující segment AC, protíná přímku LAB obsahující segment AB právě v bodě A.
-Strany: mezi každou dvojicí vrcholů je nakreslen úsečka, která tvoří jednu stranu trojúhelníku. Tento segment může být označen koncovými písmeny nebo pomocí konkrétního písmene k jeho volání. V příkladu na obrázku 2 se strana AB také nazývá „c“.
-Úhly: Mezi každou stranou se společným vrcholem vzniká úhel, jehož vrchol se shoduje s vrcholem trojúhelníku. Úhel je obecně označen řeckým písmenem, jak bylo řečeno na začátku.
Chcete-li vytvořit konkrétní trojúhelník s daným tvarem a velikostí, stačí mít jednu z následujících sad dat:
-Všechny tři strany, pro trojúhelník zcela zřejmé.
-Dvě strany a úhel mezi nimi a okamžitě zbývající strana je nakreslena.
-Dva (vnitřní) úhly a strana mezi nimi. Prodloužením jsou nakresleny dvě chybějící strany a trojúhelník je připraven.
Zápis
Obecně se v trojúhelníkové notaci používají následující konvence: vrcholy jsou označeny velkými písmeny latinky, strany malými písmeny latinky a úhly řeckými písmeny (viz obrázek 2).
Tímto způsobem je trojúhelník pojmenován podle jeho vrcholů. Například trojúhelník vlevo na obrázku 2 je trojúhelník ABC a ten vpravo trojúhelník A'B'C '.
Je také možné použít jiné notace; například úhel α na obrázku 2 je označen jako BAC. Všimněte si, že písmeno vrcholu jde uprostřed a písmena jsou napsána proti směru hodinových ručiček.
Jindy se stříška umístí k označení úhlu:
α = ∠A
Druhy trojúhelníků
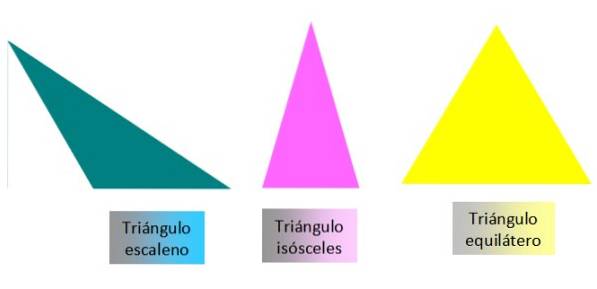
Existuje několik kritérií pro klasifikaci trojúhelníků. Nejběžnější věcí je klasifikovat je podle míry jejich stran nebo podle míry jejich úhlů. V závislosti na míře jejich stran mohou být trojúhelníky: scalenes, rovnoramenný nebo rovnostranný:
-Scalene: jeho tři strany jsou odlišné.
-Rovnoramenný: má dvě stejné strany a jednu jinou stranu.
-Rovnostranný: všechny tři strany jsou stejné.

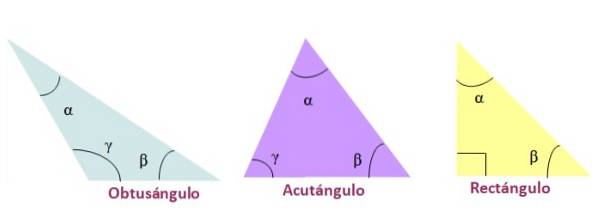
Podle míry jejich úhlů jsou trojúhelníky pojmenovány takto:
-Tupý úhel, je-li jeden z vnitřních úhlů větší než 90 °.
-Ostrý úhel, když jsou tři vnitřní úhly trojúhelníku ostré, tj. menší než 90 °
-Obdélník, v případě, že jeden z jeho vnitřních úhlů je 90 °. Strany, které tvoří 90 °, se nazývají nohy a strana naproti pravému úhlu je přepona..
Shoda trojúhelníků
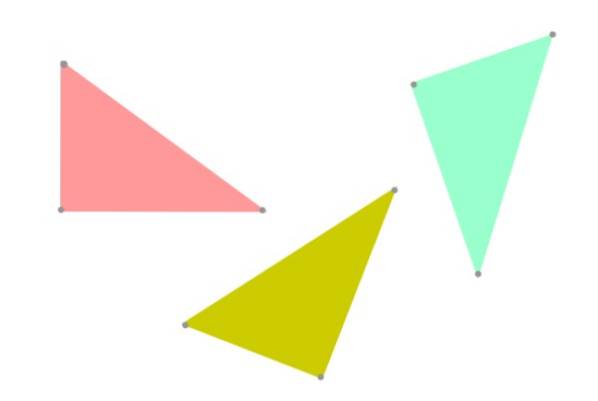
Když mají dva trojúhelníky stejný tvar a stejnou velikost, říká se, že jsou shodné. Shodnost samozřejmě souvisí s rovností, tak proč v geometrii mluvíme o „dvou shodných trojúhelnících“ místo o „dvou stejných trojúhelnících“?
Je však upřednostňováno používat termín „shoda“, abychom se drželi pravdy, protože dva trojúhelníky mohou mít stejný tvar a velikost, ale v rovině mohou být odlišně orientovány (viz obrázek 3). Z hlediska geometrie by již nebyly přísně stejné.
Kritéria shody
Dva trojúhelníky jsou shodné, pokud nastane některá z následujících situací:
-Všechny tři strany měří stejně (opět je to nejviditelnější).
-Mají dvě stejné strany a se stejným úhlem mezi nimi.
-Oba mají dva stejné vnitřní úhly a strana mezi těmito úhly měří stejnou.
Jak je vidět, jde o to, aby dva trojúhelníky splňovaly nezbytné podmínky, takže když jsou vytvořeny, jejich tvar a velikost jsou přesně stejné..
Kritéria shody jsou velmi užitečná, protože v praxi musí být nespočet kusů a mechanických částí vyrobeno sériově tak, aby jejich rozměry a tvar byly přesně stejné.
Podobnost trojúhelníků
Trojúhelník je podobný druhému, pokud mají stejný tvar, i když mají různou velikost. Abyste se ujistili, že tvar je stejný, je nutné, aby vnitřní úhly měly stejnou hodnotu a aby strany byly proporcionální..
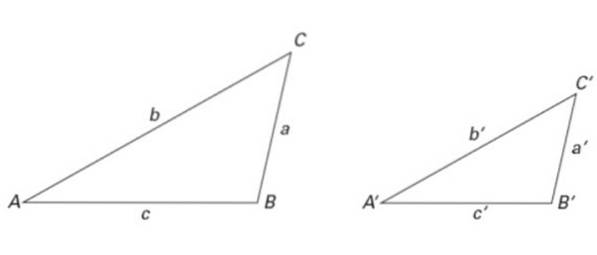
Trojúhelníky na obrázku 2 jsou také podobné, stejně jako trojúhelníky na obrázku 6. Tímto způsobem:
∠ A = ∠ A ', ∠ B = ∠ B 'a ∠ C = ∠ C '
Pokud jde o strany, platí následující poměry podobnosti:
a / a '= b / b' = c / c '
Vlastnosti
Základní vlastnosti trojúhelníků jsou následující:
-Součet vnitřních úhlů libovolného trojúhelníku je vždy 180 °.
-Pro jakýkoli trojúhelník se součet jeho vnějších úhlů rovná 360 °.
- Vnější úhel trojúhelníku se rovná součtu dvou vnitřních úhlů nesousedících s uvedeným úhlem.
Věty
Thalesova první věta
Jsou přisuzovány řeckému filozofovi a matematikovi Thalesovi z Milétu, který vyvinul několik vět souvisejících s geometrií. První z nich stanoví následující:
Pokud několik rovnoběžných linií protíná dvě příčné linie, jsou v nich určeny úměrné segmenty.
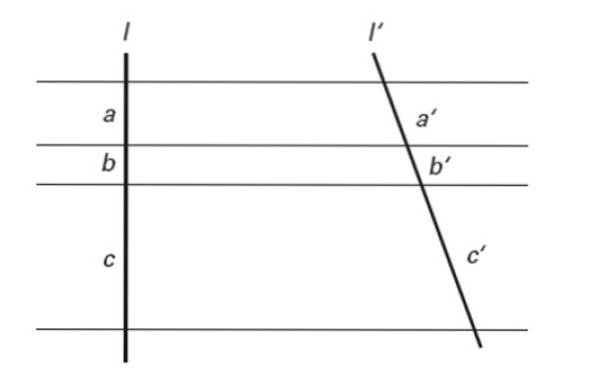
Jinými slovy:
a / a '= b / b' = c / c '
Thalesova první věta je použitelná pro trojúhelník, například máme modrý trojúhelník ABC vlevo, který je ořezán červenými rovnoběžkami vpravo:
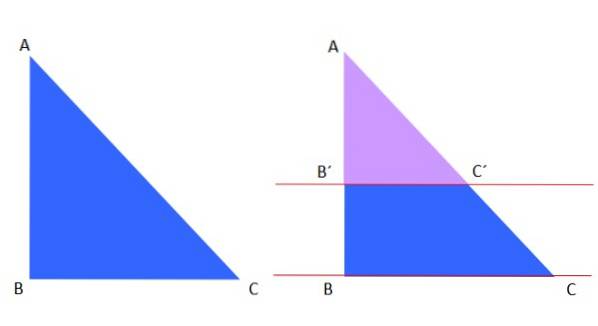
Fialový trojúhelník AB'C 'je podobný modrému trojúhelníku ABC, proto lze podle Thalesovy věty napsat následující:
AB '/ AC' = AB / AC
A je to v souladu s tím, co bylo vysvětleno dříve v segmentu podobnosti trojúhelníků. Mimochodem, rovnoběžky mohou být také svislé nebo rovnoběžné s přeponou a podobné trojúhelníky se získávají stejným způsobem.
Thalesova druhá věta
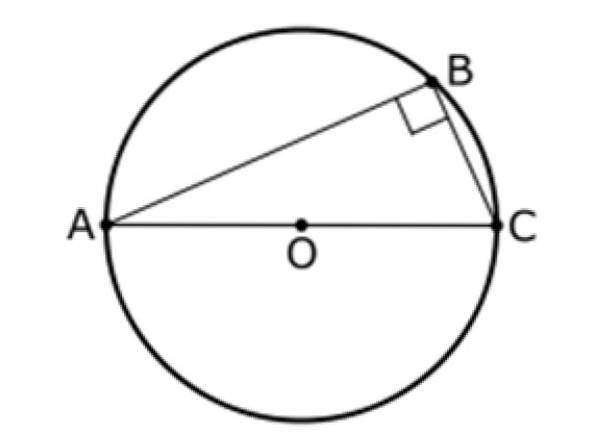
Tato věta také odkazuje na trojúhelník a kružnici se středem O, jako jsou ty, které jsou uvedeny níže. Na tomto obrázku je AC průměr obvodu a B je na něm bod, přičemž B se liší od A a B.
Thalesova druhá věta uvádí, že:
Úhel mezi segmenty AB a BC je vždy 90 °, proto je trojúhelník ABC pravý.
Pytagorova věta
Toto je jedna z nejznámějších vět v historii. Je to díky řeckému matematikovi Pythagorasovi ze Samosu (569 - 475 př. N. L.) A je použitelné pro pravý trojúhelník. Říká to:
Součet čtverců délek ramen pravoúhlého trojúhelníku se rovná délce přepony na druhou.
Vezmeme-li si jako příklad modrý trojúhelník na obrázku 8 nebo fialový trojúhelník, protože oba jsou obdélníky, pak lze konstatovat, že:
ACdva = ABdva + před naším letopočtemdva (modrý trojúhelník)
AC 'dva = AB 'dva + PŘED NAŠÍM LETOPOČTEM 'dva (fialový trojúhelník)
Plocha trojúhelníku
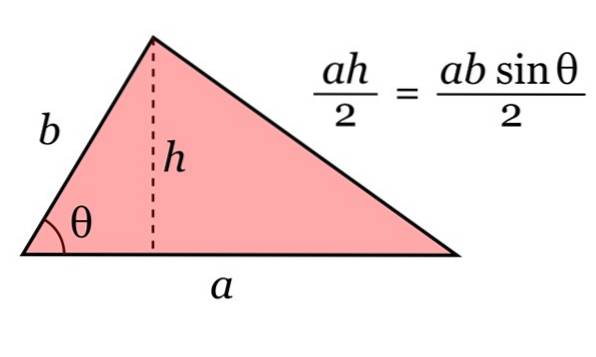
Plocha trojúhelníku je dána součinem jeho základny na a vaše výška h, děleno 2. A trigonometrií lze tuto výšku zapsat jako h = b sinθ.
Příklady trojúhelníků
Příklad 1
Říká se, že pomocí své první věty se Thalesovi podařilo změřit výšku Velké pyramidy v Egyptě, jednoho ze 7 divů starověkého světa, měřením stínu, který promítal na zem a který promítl kůl zapíchnutý do země..
Toto je nástin postupu, který následují Příběhy:
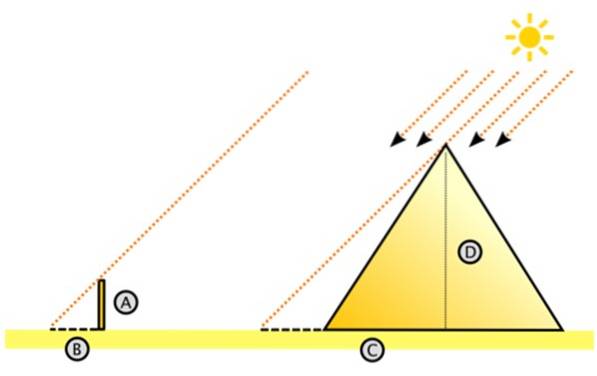
Thales správně předpokládal, že sluneční paprsky dopadají paralelně. S ohledem na to si představoval velký pravý trojúhelník vpravo.
Tam D je výška pyramidy a C je vzdálenost nad zemí měřená od středu k stínu vrženému pyramidou na pouštním dně. Měření C může být namáhavé, ale rozhodně je to jednodušší než měřit výšku pyramidy.
Na levé straně je malý trojúhelník s nohami A a B, kde A je výška kolíku zaraženého svisle do země a B je stín, který vrhá. Obě délky jsou měřitelné, stejně jako C (C se rovná délce stínu + poloviční délce pyramidy).
Podobností trojúhelníků tedy:
A / B = D / C
A výška Velké pyramidy se ukáže být: D = C. (A / B)
Příklad 2
Krovy v civilní výstavbě jsou konstrukce vyrobené z křižovaných rovných tenkých tyčí ze dřeva nebo kovu, které se používají jako podpora v mnoha budovách. Jsou také známé jako mříže, vazníky nebo mříže (krov v angličtině).
V nich jsou trojúhelníky vždy přítomné, protože tyče jsou vzájemně propojeny v bodech zvaných uzly, které mohou být pevné nebo kloubové..

Příklad 3
Metoda známá jako triangulace umožňuje získat polohu nepřístupných bodů s vědomím dalších vzdáleností, které lze snáze změřit, za předpokladu, že je vytvořen trojúhelník, který zahrnuje požadované umístění mezi jeho vrcholy..
Například na následujícím obrázku chceme vědět, kde je loď v moři, označená jako B.
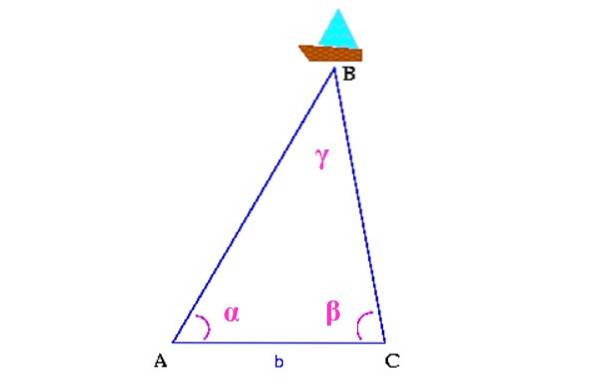
Nejprve se změří vzdálenost mezi dvěma body na pobřeží, které jsou na obrázku A a C. Dále je třeba určit úhly α a β pomocí a teodolit, zařízení sloužící k měření svislých a vodorovných úhlů.
Se všemi těmito informacemi je zabudován trojúhelník, jehož horní vrchol je loď. Zůstalo by vypočítat úhel γ pomocí vlastností trojúhelníků a vzdáleností AB a CB pomocí trigonometrie k určení polohy lodi v moři.
Výcvik
Cvičení 1
Na obrázku jsou sluneční paprsky rovnoběžné. Tímto způsobem vrhá 5 metrů vysoký strom na zem 6 metrů stín. Současně je stín budovy 40 metrů. Podle Thalesovy první věty najděte výšku budovy.
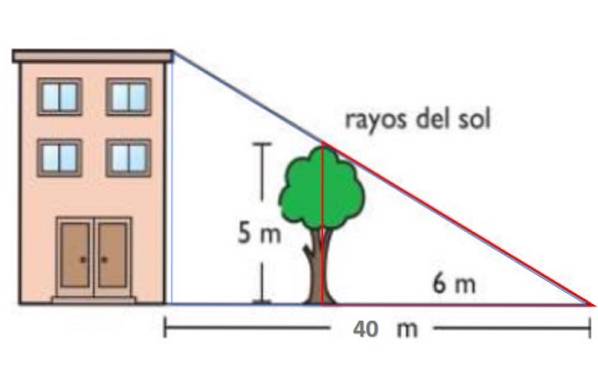
Řešení
Červený trojúhelník má strany 5 a 6 metrů, zatímco modrý má výšku H - výšku budovy - a základnu 40 metrů. Oba trojúhelníky jsou podobné, proto:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
Cvičení 2
Musíte znát vodorovnou vzdálenost mezi dvěma body NA Y B, ale jsou umístěny na velmi nerovném terénu.
O středu (strm) této země vyniká přesností 1,75 metrů vysokou. Pokud měřicí páska udává délku 26 metrů měřenou od A po výtečnost a 27 metrů od B do stejného bodu, najděte vzdálenost AB.
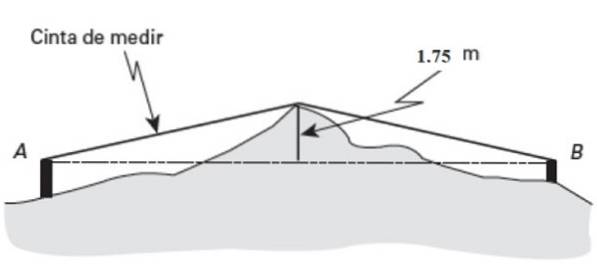
Řešení
Pythagorova věta je aplikována na jeden ze dvou pravoúhlých trojúhelníků na obrázku. Počínaje tím nalevo:
Hypotenuse = c = 26 metrů
Výška = a = 1,75 metrů
APm = (26dva - 1,75dva)1/2 = 25,94 m
Nyní použijte Pythagoras v trojúhelníku vpravo, tentokrát c = 27 metrů, a = 1,75 metrů. S těmito hodnotami:
BPm= (27dva - 1,75dva)1/2 = 26,94 m
Vzdálenost AB se zjistí přidáním těchto výsledků:
AB = 25,94 m + 26,94 m = 52,88 m.
Reference
- Baldor, J. A. 1973. Geometrie roviny a prostoru. Středoamerický kulturní.
- Barredo, D. Geometrie trojúhelníku. Obnoveno z: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matematika II. Geometrie a trigonometrie. Druhé vydání. Pearson.
- Wentworth, G. Rovinná geometrie. Obnoveno z: gutenberg.org.
- Wikipedia. Trojúhelník. Obnoveno z: es. wikipedia.org.


Zatím žádné komentáře