
Průměrné zrychlení, jak se počítá a řeší cvičení
The průměrné zrychlení nam Je to velikost, která popisuje kolísání rychlosti částice v průběhu času. Je to důležité, protože ukazuje variace, které pohyb zažívá.
Abychom tuto velikost vyjádřili matematicky, je třeba vzít v úvahu dvě rychlosti a dvě časové okamžiky, které jsou označeny jako v1 a Vdva, a ty1 a tydva.

Kombinací hodnot podle nabízené definice se získá následující výraz:
V mezinárodním systému SI jednotky pro am bude m / sdva, ačkoli jiné jednotky zahrnující délku za jednotku času na druhou budou dělat.
Například existuje km / h.s, který se čte „kilometr za hodinu a za sekundu“. Jednotka času se objeví dvakrát. Když přemýšlíte o mobilním telefonu pohybujícím se po přímce, znamená to, že za každou uplynulou sekundu zvyšuje mobil rychlost o 1 km / h. Buď ji sníží o 1 km / h za každou sekundu, která projde.
Rejstřík článků
- 1 Zrychlení, rychlost a rychlost
- 2 Jak se počítá průměrné zrychlení
- 3 známky zrychlení v jednorozměrném pohybu
- 4 Volný pád: pohyb s konstantním zrychlením
- 5 Cvičení vyřešeno
- 5.1 Odpověď
- 6 Reference
Zrychlení, rychlost a rychlost
Ačkoli je zrychlení spojeno se zvýšením rychlosti, pravdou je, že pečlivé dodržování definice se ukazuje, že jakákoli změna rychlosti znamená existenci zrychlení.
A rychlost se nemusí nutně vždy měnit. Může se stát, že mobilní telefon změní pouze směr a udržuje konstantní rychlost. Přesto stále dochází k odpovědnému zrychlení této změny.
Příkladem toho je auto, které zatáčí s konstantní rychlostí 60 km / h. Vozidlo podléhá zrychlení, které je odpovědné za změnu směru rychlosti tak, aby vůz sledoval křivku. Řidič ji aplikuje pomocí volantu.
Takové zrychlení je směrováno do středu zakřivené dráhy, aby auto z ní nešlo. Přijímá název zrychlení radiální nebo normální. Pokud by radiální zrychlení bylo náhle zrušeno, auto by již nebylo schopné dál obcházet zatáčku a pokračovalo by v přímce.
Auto pohybující se po zatáčce je příkladem pohybu ve dvou rozměrech, zatímco když jede v přímce, je jeho pohyb jednorozměrný. V tomto případě je jediným efektem zrychlení změna rychlosti vozu..
Toto zrychlení se nazývá zrychlení tangenciální. Není to výlučné pro jednorozměrný pohyb. Vůz, který obíhá zatáčku rychlostí 60 km / h, mohl současně při jízdě zrychlit na 70 km / h. V tomto případě musí řidič použít volant i plynový pedál..
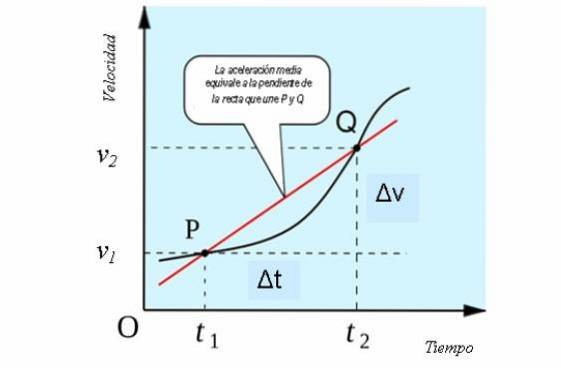
Pokud vezmeme v úvahu jednorozměrný pohyb, střední zrychlení má geometrickou interpretaci podobnou střední rychlosti, jako sklon sekanční přímky, která protíná křivku v bodech P a Q grafu rychlost vs. čas..
To lze vidět na následujícím obrázku:

Jak se počítá průměrné zrychlení
Podívejme se na několik příkladů pro výpočet průměrného zrychlení v různých situacích:
I) V určitém časovém okamžiku má mobil pohybující se po přímce rychlost + 25 km / ha o 120 sekund později má další -10 km / h. Jaké bylo průměrné zrychlení?
Odpovědět
Vzhledem k tomu, že pohyb je jednorozměrný, lze od vektorového zápisu upustit, v takovém případě:
protinebo = +25 km / h = +6,94 m / s
protiF = -10 km / h = - 2,78 m / s
Δt = 120 s
Kdykoli máte cvičení se smíšenými velikostmi, jako je tato, ve kterém jsou hodiny a sekundy, je nutné předat všechny hodnoty stejným jednotkám.

Vzhledem k tomu, že jde o jednorozměrný pohyb, odpadla vektorová notace.
II) Cyklista jede na východ rychlostí 2,6 m / s a o 5 minut později jede na jih rychlostí 1,8 m / s. Najděte jeho průměrné zrychlení.
Odpovědět
Pohyb ne je jednorozměrný, proto se použije vektorová notace. Jednotkové vektory i Y j uveďte pokyny společně s následující konvencí znaménka, což usnadní výpočet:
- Severní: +j
- Jižní: -j
- Východní: +i
- Západ: -i
protidva = - 1,8 j slečna
proti1 = + 2.6 i slečna
Δt = 5 minut = 300 sekund

Známky zrychlení v jednorozměrném pohybu
Jako vždy u průměrných nebo průměrných velikostí jsou poskytované informace globální. Neposkytují podrobnosti o tom, co se v každém okamžiku stalo s mobilem, ale to, čím přispějí, je pro popis pohybu stále cenné.
Pomocí znaků rychlosti i zrychlení je možné zjistit, zda mobilní telefon pohybující se po přímce zrychluje nebo zpomaluje. V obou situacích je přítomno zrychlení, protože rychlost se mění.
Zde jsou některé zajímavé úvahy týkající se znaků těchto dvou veličin:
- Průměrná rychlost a zrychlení, obě se stejným znaménkem, znamenají, že z globálního hlediska jde mobil rychleji a rychleji.
- Rychlost a zrychlení s různými znaky je známkou mobilního telefonu, který spíše brzdil.
Obvykle se předpokládá, že kdykoli se jedná o negativní zrychlení, mobilní zařízení brzdí. To platí, pokud je rychlost mobilního telefonu kladná. Pokud je však záporná, rychlost se ve skutečnosti zvyšuje.
Jako vždy při studiu pohybu myslete na speciální případy. Například co se stane, když je průměrné zrychlení nulové? Znamená to, že mobilní telefon vždy udržoval konstantní rychlost??
Odpověď je ne. Mobil mohl v uvažovaném intervalu měnit rychlost, ale počáteční a konečná rychlost byly stejné. V tuto chvíli nejsou známy podrobnosti toho, co se v intervalu stalo, protože průměrné zrychlení nenabízí více informací.
Co když průměrné zrychlení nam rovná se zrychlení na kdykoli v časovém intervalu? Jedná se o velmi zajímavou situaci zvanou Uniformly Varied Rectilinear Motion nebo zkráceně MRUV..
To znamená, že se rychlost v průběhu času mění rovnoměrně. Zrychlení je proto konstantní. V přírodě existuje takové hnutí, které všichni znají: volný pád.
Volný pád: pohyb s konstantním zrychlením
Je známou skutečností, že Země přitahuje objekty směrem ke svému středu a že když se člověk uvolní v určité výšce, zažije gravitační zrychlení, jehož hodnota je přibližně konstantní a rovná se 9,8 m / sdva blízko k povrchu.
Pokud odpor vzduchu nezasahuje, je pohyb svislý a je znám jako volný pád. Když je zrychlení konstantní a volba t0 = 0, rovnice pro střední zrychlení se stane:

protiF = v0 + at = gt (v0= 0)
Kde a = g = 9,8 m / sdva
Cvičení vyřešeno
Objekt je vypuštěn z dostatečné výšky. Nalezení rychlosti po 1,25 sekundě.
Odpovědět
protinebo = 0, protože objekt je zrušen, pak:
protiF = gt = 9,8 x 1,25 m / s = 12,25 m / s, směrovaný svisle k zemi. (Svislý směr dolů byl považován za kladný).
Jak se objekt přibližuje k zemi, jeho rychlost se zvyšuje o 9,8 m / s za každou uplynulou sekundu. Hmotnost objektu není zahrnuta. Dva různé předměty, spadlé ze stejné výšky a současně, vyvíjejí stejnou rychlost, jakou padají.
Reference
- Giancoli, D. Fyzika. Zásady s aplikacemi. Šesté vydání. Prentice Hall. 21-35.
- Resnick, R. (1999). Fyzický. Svazek 1. Třetí vydání ve španělštině. Mexiko. Compañía Editorial Continental S.A. de C.V. 20-34.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7ma. Edice. Mexiko. Cengage Learning Editors. 21-39.



Zatím žádné komentáře