The faktoriální souprava Jedná se o jednoduchý stroj, který se skládá z uspořádání kladek s multiplikačním účinkem síly. Tímto způsobem lze zvednout břemeno pouhým ekvivalentem zlomku hmotnosti na volný konec lana..
Skládá se ze dvou sad kladek: jedné, která je připevněna k podpěře a druhé, která vyvíjí výslednou sílu na zatížení. Kladky jsou namontovány na obecně kovovém rámu, který je drží.
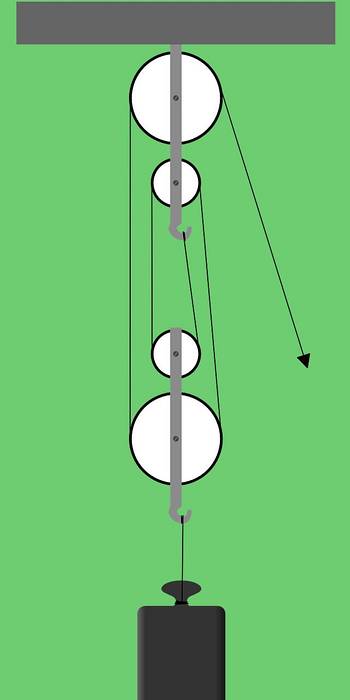
Obrázek 1 ukazuje faktoriální soupravu skládající se ze dvou skupin po dvou kladkách. Tento typ uspořádání řemenice se také nazývá sériové vybavení nebo kladkostroje.
Rejstřík článků
Abychom pochopili, proč toto uspořádání znásobuje vynaloženou sílu, začneme nejjednodušším případem, který se skládá z pevné kladky a mobilní kladky..
Na obrázku 2 máme kladku A připevněnou ke stropu pomocí podpěry. Kladka A se může volně otáčet kolem své osy. Máme také řemenici B, která má konzolu připevněnou k hřídeli řemenice, na kterou je umístěno břemeno. Kladka B má kromě toho, že se může volně otáčet kolem své osy, možnost vertikálního pohybu.
Předpokládejme, že jsme v rovnovážné situaci. Zvažte síly působící na kladku B. Osa kladky B nese celkovou hmotnost P, která směřuje dolů. Pokud by to byla jediná síla na kladku B, pak by padla, ale víme, že lano, které prochází touto kladkou, vyvíjí také dvě síly, kterými jsou T1 a T2, které směřují nahoru..
Aby zde byla translační rovnováha, musí se dvě síly nahoru rovnat hmotnosti nesené osou kladky B.
T1 + T2 = P
Ale protože kladka B je také v rotační rovnováze, pak T1 = T2. Síly T1 a T2 pocházejí z napětí působícího na strunu zvanou T.
Proto T1 = T2 = T. Nahrazením v předchozí rovnici zůstává:
T + T = P
2T = P
Což naznačuje, že napětí působící na lano je pouze poloviční hmotností:
T = P / 2
Například pokud by zatížení činilo 100 kg, stačilo by na volný konec lana vyvinout sílu 50 kg, aby se zatížení zvedlo konstantní rychlostí..
Uvažujme nyní napětí a síly působící na sestavu skládající se ze dvou uspořádání podpěr A a B se dvěma kladkami..
Podpora B má možnost vertikálního pohybu a síly na ni působící jsou:
- Hmotnost P nákladu, směřující svisle dolů.
- Dvě napětí na velké kladce a dvě napětí na malé kladce. Celkem čtyři napětí, všechna směřující vzhůru.
Aby existovala translační rovnováha, je nutné, aby síly směřující svisle nahoru se rovnaly hodnotě zatížení směřujícího dolů. To znamená, že musí být splněno:
T + T + T + T = P
To znamená, 4 T = P
Z toho vyplývá, že aplikovaná síla T na volném konci lana je pouze čtvrtinou hmotnosti v důsledku zatížení, které se chce zvednout., T = P / 4.
S touto hodnotou napětí T lze zátěž udržovat statickou nebo stoupat konstantní rychlostí. Pokud by bylo použito napětí větší než tato hodnota, pak by se zátěž zrychlila nahoru, což je podmínka, která je nutná k jejímu vyřazení z klidu..
Podle toho, co bylo vidět v předchozích případech, na každou řemenici mobilní sestavy existuje několik vzestupných sil vyvíjených lanem, které prochází řemenicí. Tato síla však nemůže být nic jiného než napětí působící na lano na volném konci.
Takže pro každou kladku mobilní sestavy bude existovat svislá síla nahoru, která se bude rovnat 2T. Ale protože v pohybující se sestavě je n kladek, vyplývá z toho, že celková síla směřující svisle nahoru je:
2 n T
Aby existovala vertikální rovnováha, je nutné, aby:
2 n T = P
síla použitá na volném konci je tedy:
T = P / (2 n)
V tomto případě lze říci, že vyvíjená síla T se na zatížení znásobí 2 nkrát.
Například pokud bychom měli faktoriální soupravu se 3 pevnými a 3 pohyblivými kladkami, počet n by se rovnal 3. Na druhé straně, pokud by zatížení bylo P = 120 kg, pak by síla působící na volný konec byla T = 120 kg / (2 * 3) = 20 kg.
Zvažte faktoriální soupravu složenou ze dvou pevných kladek a dvou pohyblivých kladek. Maximální napětí, které lano vydrží, je 60 kg. Určete, jaké je maximální zatížení, které lze umístit.
Když je břemeno v klidu nebo se pohybuje konstantní rychlostí, jeho váha P souvisí s napětím T působícím na lano pomocí následujícího vztahu:
P = 2 n T
Jelikož se jedná o soupravu se dvěma pohyblivými a dvěma pevnými kladkami, pak n = 2.
Maximální zatížení, které lze umístit, se získá, když má T maximální možnou hodnotu, která je v tomto případě 60 kg.
Maximální zatížení = 2 * 2 * 60 kg = 240 kg
Najděte vztah mezi napnutím lana a hmotností břemene ve dvouřadé faktorové soupravě, ve které je zátěž zrychlena zrychlením při.
Rozdíl v tomto příkladu s ohledem na to, co bylo dosud vidět, spočívá v tom, že je třeba vzít v úvahu dynamiku systému. Navrhujeme tedy Newtonův druhý zákon k nalezení požadovaného vztahu.
Na obrázku 4 žlutě nakreslíme síly způsobené napětím T lana. Pohyblivá část kladkostroje má celkovou hmotnost M. Bereme jako referenční systém jeden na úrovni první pevné kladky a kladný dolů.
Y1 je nejnižší poloha hřídele řemenice.
Aplikujeme druhý Newtonův zákon k určení zrychlení a1 pohyblivé části plošiny:
-4 T + Mg = M a1
Protože hmotnost nákladu je P = Mg, kde g je gravitační zrychlení, lze napsat výše uvedený vztah:
-4T + P = P (a1 / g)
Pokud bychom chtěli určit napětí působící na lano, když je určité hmotnostní zatížení P zrychleno se zrychlením a1, pak by předchozí vztah vypadal takto:
T = P (1 - a1 / g) / 4
Všimněte si, že kdyby byl systém v klidu nebo se pohyboval konstantní rychlostí, pak a1 = 0, a my bychom obnovili stejný výraz, který jsme získali v případě 2.
V tomto příkladu se používá stejné lanoví z cvičení 1 se stejným lanem, které podporuje maximálně 60 kg napětí. Určité zatížení se zvedne a zrychlí z klidu na 1 m / s za 0,5 s pomocí maximálního napětí lana. Najděte maximální hmotnost nákladu.
Použijeme výrazy získané v cvičení 2 a referenční systém na obrázku 4, ve kterém je kladný směr svisle dolů.
Zrychlení zátěže je a1 = (-1 m / s - 0 m / s) / 0,5 s = -2 m / s ^ 2.
Hmotnost břemene v kilogramové síle je dána vztahem
P = 4 T / (1 - a1 / g)
P = 4 * 60 kg / (1 + 2 / 9,8) = 199,3 kg
Toto je maximální možná hmotnost nákladu bez přetržení lana. Všimněte si, že získaná hodnota je menší než hodnota získaná v příkladu 1, ve kterém se předpokládalo, že zatížení má nulové zrychlení, tj. V klidu nebo s konstantní rychlostí..
Zatím žádné komentáře