The efektivní jaderný náboj (Zef) je přitažlivá síla vyvíjená jádrem na kterýkoli z elektronů poté, co byla snížena účinky stínění a penetrace. Pokud by takové účinky neexistovaly, elektrony by pocítily přitažlivou sílu skutečného jaderného náboje Z.
Na obrázku níže máme Bohrův atomový model pro fiktivní atom. Jeho jádro má jaderný náboj Z = + n, který přitahuje elektrony, které obíhají kolem něj (modré kruhy). Je vidět, že dva elektrony jsou na oběžné dráze blíže k jádru, zatímco třetí elektron leží od něj ve větší vzdálenosti..
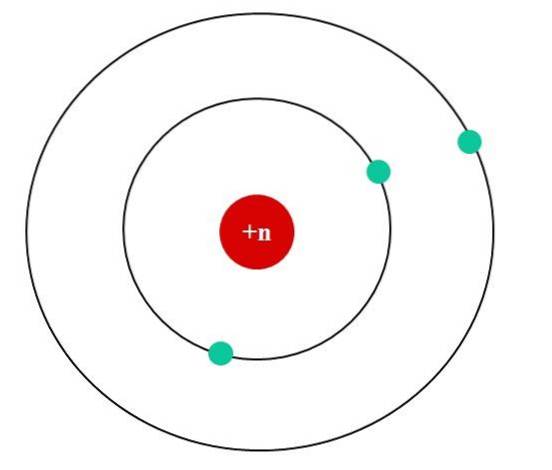
Třetí elektron obíhá a cítí elektrostatické odpuzování dalších dvou elektronů, takže jej jádro přitahuje menší silou; to znamená, že interakce jádro-elektron klesá v důsledku stínění prvních dvou elektronů.
První dva elektrony tedy pociťují přitažlivou sílu náboje + n, ale třetí místo toho zažívá efektivní jaderný náboj + (n-2)..
Uvedený Zef by však byl platný pouze v případě, že by vzdálenosti (poloměr) k jádru všech elektronů byly vždy konstantní a určité, lokalizující jejich záporné náboje (-1).
Rejstřík článků
Protony definují jádra chemických prvků a elektrony definují svou identitu v rámci souboru charakteristik (skupiny periodické tabulky)..
Protony zvyšují jaderný náboj Z rychlostí n + 1, což je kompenzováno přidáním nového elektronu ke stabilizaci atomu.
Jak se zvyšuje počet protonů, jádro je „pokryto“ dynamickým mrakem elektronů, ve kterém jsou oblasti, kterými cirkulují, definovány pravděpodobnostním rozdělením radiálních a úhlových částí vlnových funkcí (orbitalů).
Z tohoto přístupu elektrony neobíhají v definované oblasti prostoru kolem jádra, ale spíše, jako lopatky rychle se otáčejícího ventilátoru, stírají do tvarů známých orbitalů s, p, d a f.
Z tohoto důvodu je záporný náboj -1 elektronu distribuován těmi oblastmi, kterými pronikají orbitaly; čím větší je penetrační účinek, tím větší je efektivní jaderný náboj, který uvedený elektron zažije na oběžné dráze.
Podle výše uvedeného vysvětlení elektrony ve vnitřních skořápkách nepřispívají nábojem 1 ke stabilizujícímu odpuzování elektronů ve vnějších skořápkách..
Toto jádro (skořápky dříve naplněné elektrony) však slouží jako „zeď“, která brání přitažlivé síle jádra dosáhnout vnějších elektronů..
Toto se nazývá efekt obrazovky nebo efekt stínění. Také ne všechny elektrony ve vnějších skořápkách zažívají stejnou velikost tohoto účinku; například pokud obsadíte orbitál, který má vysoce pronikavý charakter (tj. který se pohybuje velmi blízko jádra a dalších orbitalů), budete cítit vyšší.
Výsledkem je řád energetické stability jako funkce těchto Zefů pro orbitaly: s To znamená, že orbitál 2p má vyšší energii (méně stabilizovanou nábojem jádra) než orbitál 2s.. Čím horší je penetrační účinek orbitálu, tím menší bude jeho stínící účinek na zbytek vnějších elektronů. Orbitaly d a f ukazují mnoho otvorů (uzlů), kde jádro přitahuje další elektrony. Za předpokladu, že jsou lokalizovány záporné náboje, vzorec pro výpočet Zef pro jakýkoli elektron je: Zef = Z - σ V tomto vzorci σ je ochranná konstanta určená elektrony jádra. Je to proto, že nejvzdálenější elektrony teoreticky nepřispívají ke stínění vnitřních elektronů. Jinými slovy, 1 sdva stínící elektron 2 s1, ale 2 s1 nestíní Z elektrony 1 sdva. Pokud Z = 40, zanedbáním zmíněných efektů, pak poslední elektron zažije Zef rovný 1 (40-39). Slaterovým pravidlem je dobrá aproximace hodnot Zef pro elektrony v atomu. Chcete-li jej použít, postupujte podle následujících pokynů: 1- Elektronická konfigurace atomu (nebo iontu) by měla být napsána následovně: (1s) (2s 2p) (3s 3p) (3d) (4s 4p) (4d) (4f)… 2 - Elektrony, které jsou napravo od uvažovaného, nepřispívají k efektu stínění. 3 - Elektrony, které jsou ve stejné skupině (označené v závorkách), poskytují 0,35 náboje elektronu, pokud se nejedná o skupinu 1 s, místo toho je 0,30. 4 - Pokud elektron zaujímá orbitál s nebo p, pak všechny orbitály n-1 přispívají 0,85 a všechny orbitály n-2 jsou jednotkou. 5 - V případě, že elektron zabírá orbitál d nebo f, přispívají všichni nalevo k jedné jednotce. Po Slaterově způsobu reprezentace je elektronická konfigurace Be (Z = 4): (1 s.)dva) (2 s.)dva2 str0) Jelikož v orbitálu jsou dva elektrony, jeden z nich přispívá ke stínění druhého a orbitál 1 s je n-1 orbitálu 2 s. Při vývoji algebraického součtu máme následující: (0,35) (1) + (0,85) (2) = 2,05 0,35 pocházelo z elektronu 2 s a 0,85 ze dvou elektronů 1 s. Nyní použijeme Zefův vzorec: Zef = 4 - 2,05 = 1,95 Co to znamená? To znamená, že elektrony ve 2s jsou na oběžné drázedva zažít poplatek +1,95, který je přitahuje směrem k jádru, spíše než skutečný poplatek +4. Opět pokračuje jako v předchozím příkladu: (1 s.)dva) (2 s.)dva2 str6) (3 s.)dva3p3) Nyní je algebraický součet vyvinut pro určení σ: (, 35) (4) + (0,85) (8) + (1) (2) = 10,2 Zef je tedy rozdíl mezi σ a Z: Zef = 15-10,2 = 4,8 Na závěr poslední 3p elektrony3 zažijí třikrát méně zátěže než skutečné. Je třeba také poznamenat, že podle tohoto pravidla jsou 3s elektronydva zažijte stejný Zef, výsledek, který by o něm mohl vyvolat pochybnosti. Existují však úpravy Slaterova pravidla, které pomáhají přiblížit vypočítané hodnoty skutečných..Jak to vypočítat?
Slaterovo pravidlo
Příklady
Určete Zef pro elektrony na 2s oběžné drázedva v berýliu
Určete Zef pro elektrony na 3p oběžné dráze3 fosforu
Reference
Zatím žádné komentáře