
Vlastnosti těžiště, výpočet, příklady
The gravitační centrum těla měřitelné velikosti je bod, kde se jeho váha považuje za aplikovanou. Jedná se tedy o jeden ze základních pojmů statiky.
První přístup v problémech elementární fyziky spočívá v předpokladu, že jakýkoli objekt se chová jako hmota bodu, to znamená, že nemá žádné rozměry a veškerá hmota je soustředěna do jediného bodu. To platí pro skříň, auto, planetu nebo subatomární částice. Tento model je známý jako částicový model.

Toto je samozřejmě aproximace, která funguje velmi dobře pro mnoho aplikací. Není snadné uvážit individuální chování tisíců a milionů částic, které může obsahovat jakýkoli objekt.
Skutečné rozměry věcí však musí být vzaty v úvahu, mají-li být dosaženy výsledky, které se blíží realitě. Jelikož jsme obecně v blízkosti Země, všudypřítomná síla na každé tělo je přesně váha.
Rejstřík článků
- 1 Úvahy o nalezení těžiště
- 2 Jak se počítá těžiště?
- 3 Vlastnosti
- 3.1 - Nalezení těžiště těla ve statické rovnováze
- 3.2 - Vyřešený příklad
- 4 Rozdíl od těžiště
- 5 Příklady těžiště
- 5.1 Těžiště nepravidelných předmětů
- 5.2 Vyvažování objektů
- 6 Reference
Úvahy o nalezení těžiště
Pokud se má brát v úvahu velikost těla, kde konkrétně se má váha použít? Máte-li libovolně spojitý objekt, jeho váha je a rozložená síla mezi každou ze svých základních částic.
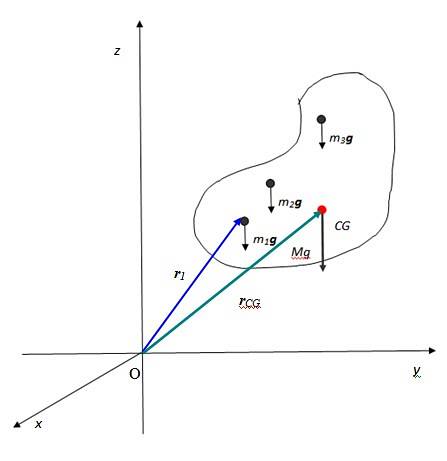
Nechť jsou tyto částice m1, mdva, m3… Každý z nich zažívá svou odpovídající gravitační sílu m1g, mdvag, m3g…, všechny paralelně. Je tomu tak, protože gravitační pole Země je v drtivé většině případů považováno za konstantní, vzhledem k tomu, že objekty jsou ve srovnání s velikostí planety malé a jsou blízko jejího povrchu..
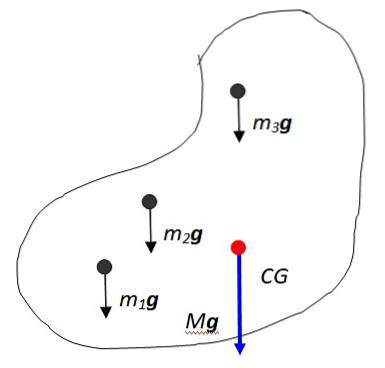
Výsledkem vektorového součtu těchto sil je váha objektu, aplikovaná na bod zvaný těžiště označený na obrázku jako CG, který se potom shoduje s Mass centrum. Těžiště je zase bod, kde lze veškerou hmotu považovat za koncentrovanou.
Výsledná váha má velikost Mg kde M je celková hmotnost objektu a je samozřejmě směrována svisle ke středu Země. Součtový zápis je užitečný pro vyjádření celkové hmotnosti těla:
Těžiště se ne vždy shoduje s hmotným bodem. Například CG prstence je v jeho geometrickém středu, kde není samotná hmota. I přesto, pokud chcete analyzovat síly působící na obruč, musíte použít váhu na tento přesný bod.
V případech, kdy má objekt libovolný tvar, je-li homogenní, lze jeho těžiště stále vypočítat nalezením těžiště nebo těžiště postavy.
Jak vypočítáte těžiště?
V zásadě platí, že pokud se těžiště (CG) a těžiště (cm) shodují, protože gravitační pole je rovnoměrné, lze vypočítat cm a aplikovat na něj váhu.
Uvažujme o dvou případech: prvním je případ, kdy je rozdělení hmoty diskrétní; to znamená, že každou hmotu, která tvoří systém, lze spočítat a přiřadit jí číslo i, jak bylo provedeno v předchozím příkladu.
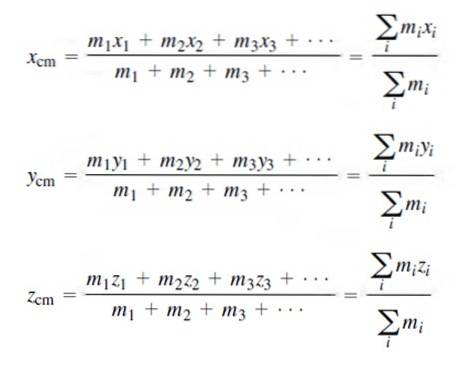
Souřadnice těžiště pro diskrétní rozdělení hmoty jsou:
Součet všech hmot se přirozeně rovná celkové hmotnosti soustavy M, jak je uvedeno výše..
Tři rovnice jsou redukovány na kompaktní formu uvažováním vektoru rcm nebo vektor polohy těžiště:
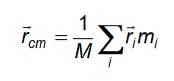
A v případě kontinuálního rozdělení hmoty, kde částice mají rozdílnou velikost a nelze je rozlišit, aby je bylo možné spočítat, je součet nahrazen integrálem, který je vytvořen přes objem obsazený daným objektem:
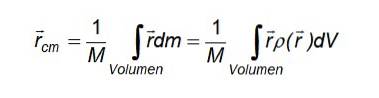
Kde r je polohový vektor diferenciální hmoty dm a definice hmotnostní hustoty byla použita k vyjádření hmotnostního rozdílu dm obsažené v objemovém diferenciálu dV:
Vlastnosti
Některé důležité úvahy o těžišti jsou následující:
- Ačkoli je pro stanovení pozic vyžadován referenční systém, těžiště nezávisí na výběru provedeném systémem, protože je to vlastnost objektu.
- Pokud má objekt osu nebo rovinu symetrie, těžiště je na této ose nebo rovině. Využití této okolnosti šetří čas výpočtu.
- Všechny vnější síly působící na objekt lze aplikovat na těžiště. Sledování pohybu tohoto bodu dává globální představu o pohybu objektu a usnadňuje práci při studiu jeho chování..
-Nalezení těžiště těla ve statické rovnováze
Předpokládejme, že chcete, aby tělo na předchozím obrázku bylo ve statické rovnováze, to znamená, že se nepřekládá ani neotáčí kolem libovolné osy otáčení, která může být O.

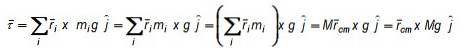
-Pracoval příklad
Tenká tyč stejnoměrného materiálu je 6 m dlouhá a váží 30 N. Na levém konci je zavěšeno závaží 50 N a na pravém konci závaží 20 N. Najít: a) velikost síly vzhůru nutná k udržení rovnováhy tyče, b) těžiště soustavy.
Řešení
Silový diagram je znázorněn na následujícím obrázku. Hmotnost tyče se aplikuje na její těžiště, které se shoduje s jejím geometrickým středem. Jediným rozměrem lišty, která se bere v úvahu, je její délka, protože prohlášení informuje, že je tenká.
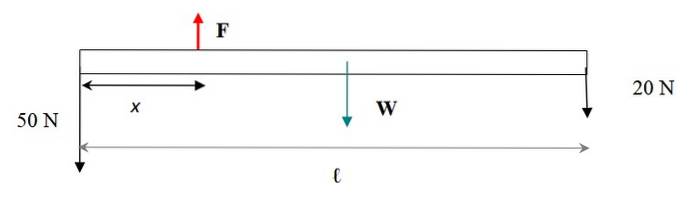
Aby systém bar + závaží zůstal v translační rovnováze, musí být součet sil nulový. Síly jsou vertikální, pokud uvažujeme nahoru se znaménkem + a dolů se znaménkem - pak:
F- 50 - 20 - 30 N = 0
F = 100 N
Tato síla zaručuje překladovou rovnováhu. Vezmeme torzní momenty všech sil vzhledem k ose, která prochází levým koncem systému, a použijeme definici:
t = r x F
Momenty všech těchto sil kolem vybraného bodu jsou kolmé na rovinu prutu:
tF = xF = 100x
tŽ = - (l / 2) mg = -3m. 30 N = -90 N.m
t1 = 0 (protože síla 50 N prochází vybranou osou otáčení a nevyvíjí moment)
tdva = -lFdva = 6 m. 20 N = -120 N.m
Proto:
100 x -90 - 120 N.m = 0
x = 2,10 m
Těžiště sady tyčí + závaží se nachází 2,10 m od levého konce tyče.
Rozdíl od těžiště
Těžiště se shoduje s těžištěm, jak je naznačeno, pokud je gravitační pole Země konstantní pro všechny uvažované body objektu. Gravitační pole Země není nic jiného než známá a známá hodnota g = 9,8 m / sdva směřující svisle dolů.
Přestože se hodnota g liší podle zeměpisné šířky a nadmořské výšky, obvykle tyto objekty neovlivňují většinu času. Bylo by velmi odlišné, kdybyste uvažovali o velkém tělese v blízkosti Země, například o asteroidu, který je velmi blízko planety.
Asteroid má své vlastní těžiště, ale jeho těžiště by se s tím již nemuselo shodovat, protože G pravděpodobně by došlo k podstatným odchylkám velikosti vzhledem k velikosti asteroidu a vzhledem k tomu, že váhy každé částice nemusí být paralelní.
Dalším zásadním rozdílem je, že těžiště se nachází bez ohledu na to, zda na předmět působí síla zvaná váha. Jedná se o vnitřní vlastnost objektu, která nám odhaluje, jak je jeho hmota distribuována ve vztahu k jeho geometrii.
Těžiště existuje bez ohledu na to, zda je nebo není aplikována hmotnost. A nachází se ve stejné poloze, i když se objekt pohybuje na jinou planetu, ve které je gravitační pole odlišné..
Na druhou stranu je těžiště jasně spojeno s aplikací hmotnosti, jak jsme viděli v předchozích odstavcích..
Příklady těžiště
Těžiště nepravidelných předmětů
Je velmi snadné zjistit, kde je těžiště nepravidelného předmětu, například šálku. Nejprve je zavěšen z kteréhokoli bodu a odtud je nakreslena svislá čára (na obrázku 5 je to fuchsiová čára na levém obrázku).
Poté se zavěsí z jiného bodu a nakreslí se nová svislá čára (tyrkysová čára na pravém obrázku). Průsečík obou čar je těžiště pohárku.

Vyvažování objektů
Pojďme analyzovat stabilitu nákladního vozidla jedoucího po silnici. Pokud je těžiště nad základnou vozíku, vozík se nepřeklopí. Obrázek vlevo je nejstabilnější pozice.
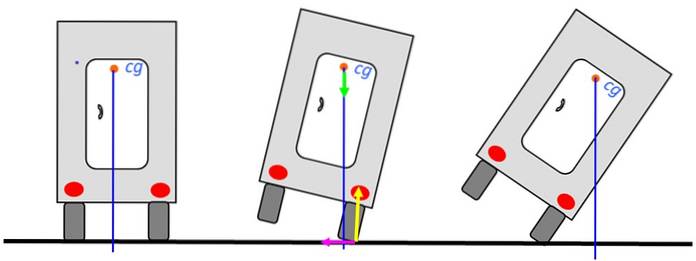
I když je nákladní vozidlo nakloněno doprava, bude se moci vrátit do stabilní rovnovážné polohy, jako na středním obrázku, protože vertikální stále prochází základnou. Když však tato čára projde ven, nákladní vůz se převrátí.
Diagram ukazuje síly na otočném bodě: normální ve žluté, váha v zelené a statické tření doleva ve fuchsii. Normály a tření působí na osu otáčení, takže nevyvíjejí točivý moment. Proto nepřispějí k převrácení vozíku.
Hmotnost zůstává, která vyvíjí točivý moment, naštěstí proti směru hodinových ručiček, a která má tendenci vrátit vozík do rovnovážné polohy. Všimněte si, že svislá čára prochází nosnou plochou, kterou je pneumatika.
Když je vozík v krajní pravé poloze, změní se točivý moment hmotnosti ve směru hodinových ručiček. Nelze čelit jindy, vozík se převrátí.
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.… Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Fyzický. Sv. 1. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Základy fyziky. Pearson. 146-155.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání 1.340-346.



Zatím žádné komentáře