The koeficient restituce je podíl mezi relativní rychlostí ústupu a relativní rychlostí přiblížení dvou kolidujících těles. Když jsou těla po srážce sjednocena, je tento podíl nulový. A jednotka stojí za to v případě, že srážka je dokonale elastická.
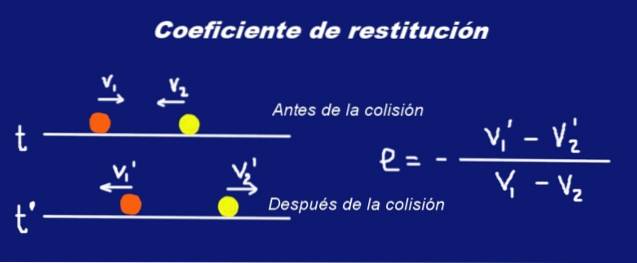
Předpokládejme dvě pevné sféry hmoty M1 a mše M2 respektive, které utrpěly kolizi. Těsně před srážkou měly koule rychlosti V1 Y V2 s ohledem na určitý setrvačný referenční systém. Hned po srážce se jejich rychlost změní na V1 ' Y V2 '.
Dopis byl vložen tučné písmo v rychlostech k označení, že se jedná o vektorové veličiny.
Experimenty naznačují, že každá kolize splňuje následující vztah:
V1 ' - V2 '= -a (V1 - V2)
Kde a je reálné číslo mezi 0 a 1, které se říká koeficient restituce srážky. Výše uvedený výraz je interpretován takto:
Relativní rychlost dvou částic před srážkou je úměrná relativní rychlosti dvou částic po srážce, konstanta úměrnosti je (-e), kde e je koeficient restituce srážky.
Rejstřík článků
Užitečnost tohoto koeficientu spočívá ve znalosti stupeň nepružnosti srážky. V případě, že srážka je dokonale elastická, bude koeficient 1, zatímco při zcela nepružné srážce bude koeficient 0, protože v tomto případě je relativní rychlost po srážce nulová..
Naopak, pokud jsou známy koeficient restituce srážky a rychlosti částic před ní, pak lze předpovědět rychlosti po srážce..
Při kolizích existuje kromě vztahu, který stanoví koeficient restituce, ještě jeden základní vztah, kterým je zachování hybnosti.
Hybnost p částice nebo hybnosti, jak se jí také říká, je produktem hmoty M částice její rychlostí PROTI. To znamená: hybnost p je vektorová veličina.
Při srážkách lineární hybnost P systému je stejný těsně před a těsně po srážce, protože vnější síly jsou zanedbatelné ve srovnání s krátkými, ale intenzivními silami vnitřní interakce během srážky. Zachování hybnosti však nestačí P systému vyřešit obecný problém kolize.
V dříve zmíněném případě, zachování dvou lineárních hybností M1 a M2, je zachování lineární hybnosti napsáno následovně:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Neexistuje způsob, jak vyřešit problém s kolizí, pokud není znám restituční koeficient. Zachování hybnosti, i když je to nutné, není dostatečné k předpovědi rychlostí po srážce.
Když problém uvádí, že těla po kolizi zůstávají v pohybu, implicitně říká, že restituční koeficient je 0.
Další důležitou fyzikální veličinou, která se účastní srážek, je energie. Během kolizí dochází k výměnám kinetické energie, potenciální energie a dalších druhů energie, jako je tepelná energie.
Před a po srážce je potenciální energie interakce prakticky nulová, takže energetická bilance zahrnuje kinetickou energii částic před a po a množství Q zvaná rozptýlená energie.
Pro dvě kolidující hmotné koule M1 a M2 se energetická bilance před a po srážce zapíše takto:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q
Pokud jsou interakční síly během srážky čistě konzervativní, stane se, že celková kinetická energie srážejících se částic je zachována, to znamená, že je to stejné před i po srážce (Q = 0). Když k tomu dojde, říká se, že kolize je dokonale elastická..
V případě elastických kolizí se žádná energie nerozptýlí. Koeficient restituce navíc splňuje: e = 1.
Naopak v nepružných srážkách Q ≠ 0 a 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
Aby bylo možné problém s kolizí dokonale určit, je nutné znát koeficient restituce nebo alternativně množství energie rozptýlené během kolize..
Koeficient restituce závisí na povaze a typu interakce mezi dvěma těly během srážky..
Relativní rychlost těles před srážkou definuje intenzitu interakce, a tedy její vliv na restituční koeficient..
Abychom ilustrovali, jak se vypočítá koeficient restituce kolize, vezmeme jednoduchý případ:
Předpokládejme kolizi dvou sfér hmot M1 = 1 kg Y M2 = 2 kg pohyb po rovné kolejnici bez tření (jako na obrázku 1).
První koule zasáhne počáteční rychlostí V1 = 1 m / s na druhém, který je původně v klidu, to znamená V2 = 0 m / s.
Po srážce se pohybují takto: první se zastaví (V1 '= 0 m / s) a druhý se pohybuje rychlostí doprava V2 '= 1/2 m / s.
Pro výpočet restitučního koeficientu v této kolizi použijeme vztah:
V1 ' - V2 ' = -a ( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
Při jednorozměrné srážce dvou sfér předchozí části byl vypočítán jejich restituční koeficient, jehož výsledkem bylo e = ½ .
Protože srážka e ≠ 1 není elastická, to znamená, že kinetická energie systému není zachována a existuje určité množství rozptýlené energie Q (například zahřátí koulí v důsledku kolize).
Určete hodnotu energie rozptýlené v Joulech. Vypočítejte také procentuální podíl rozptýlené energie.
Počáteční kinetická energie koule 1 je:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J
zatímco sféra 2 je nulová, protože je zpočátku v klidu.
Pak je počáteční kinetická energie systému Ki = ½ J.
Po srážce se pohybuje pouze druhá koule rychlostí V2 '= ½ m / s, takže konečná kinetická energie systému bude:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J
To znamená, že energie rozptýlená při srážce je:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J
A zlomek energie rozptýlené při této srážce se vypočítá takto:
f = Q / Ki = ¼ / ½ = 0,5, to znamená, že 50% energie systému bylo rozptýleno kvůli nepružné kolizi, jejíž koeficient restituce je 0,5.
Zatím žádné komentáře