
Konstanta integračního významu, výpočtu a příkladů

The konstanta integrace Jedná se o přidanou hodnotu výpočtu antiderivativ nebo integrálů, slouží k reprezentaci řešení, která tvoří primitiv funkce. Vyjádřete inherentní nejednoznačnost, kde libovolná funkce má nekonečný počet primitiv.
Například pokud vezmeme funkci: f (x) = 2x + 1 a dostaneme její primitivní funkci:
∫ (2x + 1) dx = xdva + X + C ; Kde C je konstanta integrace a graficky představuje vertikální překlad mezi nekonečnými možnostmi primitivu. Je správné říci, že (xdva + x) je A primitivů f (x).
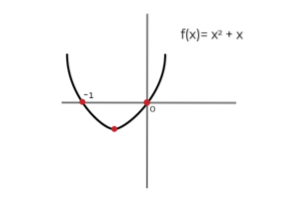
Stejným způsobem můžeme definovat a (xdva + X + C ) jako primitiv f (x).
Rejstřík článků
- 1 Inverzní vlastnost
- 2 Neurčitý integrál
- 3 Další významy konstanty integrace
- 4 Jak se počítá integrační konstanta?
- 5 příkladů
- 5.1 Příklad 1
- 5.2 Příklad 2
- 5.3 Příklad 3
- 6 Navrhovaná cvičení
- 6.1 Cvičení 1
- 6.2 Cvičení 2
- 6.3 Cvičení 3
- 6.4 Cvičení 4
- 7 Reference
Reverzní vlastnost
Je možné poznamenat, že odvozením výrazu (xdva + x) získá se funkce f (x) = 2x + 1. Důvodem je inverzní vlastnost existující mezi derivací a integrací funkcí. Tato vlastnost umožňuje získat integrační vzorce počínaje diferenciací. Což umožňuje ověření integrálů pomocí stejných derivací.
Nicméně (xdva + x) není jediná funkce, jejíž derivace se rovná (2x + 1).
- d (Xdva + x) / dx = 2x + 1
- d (Xdva + x + 1) / dx = 2x + 1
- d (Xdva + x + 2) / dx = 2x + 1
- d (Xdva + x + 3) / dx = 2x + 1
- d (Xdva + X + C) / dx = 2x + 1
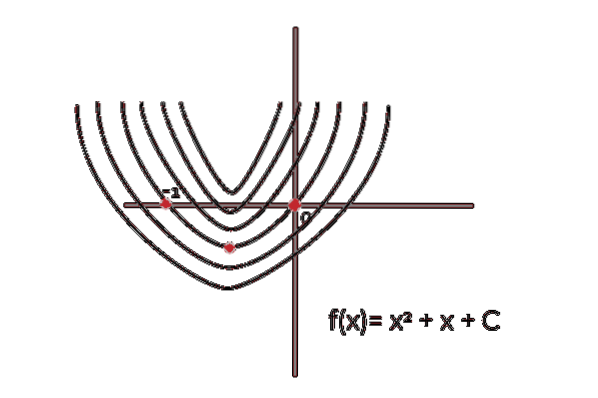
Kde 1, 2, 3 a 4 představují konkrétní primitiva f (x) = 2x + 1. Zatímco 5 představuje neurčitý nebo primitivní integrál f (x) = 2x + 1.
Primitiva funkce jsou dosažena pomocí primitivní funkce nebo integrálního procesu. Kde F bude primitivem f, pokud platí následující
- y = ∫ f (x) dx = F (x) + C; C = konstanta integrace
- F '(x) = f (x)
Je vidět, že funkce má na rozdíl od svých nekonečných primitiv vyplývajících z integrace jedinou derivaci.
Neurčitý integrál
∫ f (x) dx = F (x) + C
Odpovídá rodině křivek se stejným vzorem, které zažívají nesoulad v hodnotě obrazů každého bodu (x, y). Každá funkce, která splňuje tento vzor, bude samostatným primitivem a sada všech funkcí je známá jako neurčitý integrál.
Hodnota konstanta integrace bude ten, který v praxi odlišuje každou funkci.
The konstanta integrace navrhuje vertikální posun ve všech grafech představujících primitiva funkce. Kde je pozorován paralelismus mezi nimi a skutečnost, že C je hodnota posunutí.
Podle běžných postupů konstanta integrace označuje se písmenem „C“ po přidání, i když v praxi nezáleží na tom, zda je konstanta přidána nebo odečtena. Jeho skutečnou hodnotu lze najít různými způsoby podle různých počáteční podmínky.
Další významy konstanty integrace
Už se mluvilo o tom, jak konstanta integrace se uplatňuje v oboru integrální počet; Představující rodinu křivek, které definují neurčitý integrál. Ale mnoho dalších věd a oborů přiřadilo velmi zajímavé a praktické hodnoty konstanta integrace, které usnadnily vývoj několika studií.
V fyzický konstanta integrace může mít více hodnot v závislosti na povaze dat. Velmi častým příkladem je znalost funkce V (t) který představuje rychlost částice versus čas t. Je známo, že při výpočtu primitivu V (t) se získá funkce R (t) který představuje pozice částice versus čas.
The konstanta integrace bude představovat hodnotu počáteční polohy, tj. v čase t = 0.
Podobně, pokud je funkce známa Na) který představuje akcelerace částice versus čas. Primitiv A (t) bude mít za následek funkci V (t), kde konstanta integrace bude hodnota počáteční rychlosti V0.
V ekonomika, získáním integrace primitivu nákladové funkce. The konstanta integrace bude představovat fixní náklady. A tolik dalších aplikací, které si zaslouží diferenciální a integrální počet.
Jak se počítá integrační konstanta?
Pro výpočet konstanta integrace, vždy bude nutné znát počáteční podmínky. Které jsou zodpovědné za definování, který z možných primitiv je odpovídající.
V mnoha aplikacích se s ní zachází jako s nezávislou proměnnou v čase (t), kde je konstanta C bere hodnoty, které definují počáteční podmínky konkrétního případu.
Vezmeme-li počáteční příklad: ∫ (2x + 1) dx = xdva + X + C
Platnou počáteční podmínkou může být podmínka, že graf projde určitou souřadnicí. Například je známo, že primitivní (xdva + X + C) prochází bodem (1, 2)
F (x) = xdva + X + C; toto je obecné řešení
F (1) = 2
V této rovnosti dosadíme obecné řešení
F (1) = (1)dva + (1) + C = 2
Odkud to snadno vyplývá C = 0
Tímto způsobem je odpovídající primitiv pro tento případ F (x) = xdva + X
Existuje několik typů numerických cvičení, se kterými pracuje konstanty integrace. Ve skutečnosti diferenciální a integrální počet nepřestává být používán v současných vyšetřováních. Na různých akademických úrovních je lze nalézt; od počátečního výpočtu, přes fyziku, chemii, biologii, ekonomii atd.
To je také vidět ve studii o diferenciální rovnice, Kde konstanta integrace Může to mít různé hodnoty a řešení, a to díky mnohonásobným derivacím a integracím, které se v této záležitosti provádějí.
Příklady
Příklad 1
- 30 metrů vysoké dělo vystřelí projektil svisle nahoru. Je známo, že počáteční rychlost střely je 25 m / s. Rozhodni se:
- Funkce, která definuje polohu střely s ohledem na čas.
- Čas letu nebo okamžik, kdy částice dopadne na zem.
Je známo, že při rovnoměrně proměnlivém přímočarém pohybu je zrychlení konstantní hodnotou. To je případ vypuštění střely, kde zrychlení bude gravitační
g = - 10 m / sdva
Je také známo, že zrychlení je druhou derivací polohy, což naznačuje dvojitou integraci v rozlišení cvičení, čímž se získají dvě konstanty integrace.
A (t) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
Počáteční podmínky cvičení ukazují, že počáteční rychlost je V0 = 25 m / s. To je rychlost v okamžiku času t = 0. Tímto způsobem je zajištěno, že:
V (0) = 25 = -10 (0) + C1 Y C1 = 25
Definovaná funkce rychlosti
V (t) = -10t + 25; Podobnost s vzorcem MRUV (VF = V0 + a x t)
Homologním způsobem přistoupíme k integraci funkce rychlosti, abychom získali výraz, který definuje polohu:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5tdva + 25t + Cdva
R (t) = -5 tdva + 25t + Cdva (primitiv pozice)
Počáteční poloha R (0) = 30 m je známá. Poté se vypočítá konkrétní primitivum střely.
R (0) = 30m = -5 (0)dva + 25 (0) + Cdva . Kde Cdva = 30
První část je od té doby vyřešena R (t) = -5 tdva + 25t + 30 ; Tento výraz je homologní s posunovacím vzorcem v MRUV R (t) = R0 + PROTI0t - gtdva/dva
Pro druhou část je třeba vyřešit kvadratickou rovnici: -5tdva + 25t + 30 = 0
Jelikož je to podmínkou pro to, aby částice dosáhla země (poloha = 0)
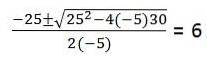
Ve skutečnosti nám rovnice 2. stupně dává 2 řešení T: 6, -1. Hodnota t = -1 je ignorována, protože jde o časové jednotky, jejichž doména neobsahuje záporná čísla.
Tímto způsobem je vyřešen druhý úsek, kde je doba letu rovna 6 sekundám.
Příklad 2
- Najděte primitivní f (x), které splňuje počáteční podmínky:
- f "(x) = 4; f '(2) = 2; f (0) = 7
S informací o druhé derivaci f "(x) = 4 začíná proces antiiderivace
f '(x) = ∫f "(x) dx
∫4 dx = 4x + C1
Poté, když známe podmínku f '(2) = 2, pokračujeme:
4 (2) + C.1 = 2
C1 = -6 a f '(x) = 4x - 8
Stejným způsobem postupujte u druhé konstanta integrace
f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2xdva - 8x + C.dva
Počáteční podmínka f (0) = 7 je známá a pokračujeme:
2 (0)dva - 8 (0) + C.dva = 7
Cdva = 7 a f (x) = 2xdva - 8x + 7
- f "(x) = xdva ; f '(0) = 6; f (0) = 3
Podobně jako v předchozím problému definujeme první derivace a původní funkci z počátečních podmínek.
f '(x) = ∫f "(x) dx
∫ (xdva) dx = (x3/ 3) + C.1
S podmínkou f '(0) = 6 pokračujeme:
(03/ 3) + C.1 = 6; Kde1 = 6 a f '(x) = (x3/ 3) + 6
Pak druhý konstanta integrace
f (x) = ∫f '(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + C.dva
Počáteční podmínka f (0) = 3 je známá a pokračujeme:
[(0)4/ 12] + 6 (0) + C.dva = 3; Kdedva = 3
Tím získáme primitivní partikulár
f (x) = (X4/ 12) + 6x + 3
Příklad 3
- Definujte primitivní funkce dané derivacemi a bodem v grafu:
- dy / dx = 2x - 2, která prochází bodem (3, 2)
Je důležité si uvědomit, že derivace odkazují na sklon přímky tečné ke křivce v daném bodě. Není-li správné předpokládat, že se graf derivace dotýká uvedeného bodu, protože to patří ke grafu primitivní funkce.
Tímto způsobem vyjádříme diferenciální rovnici takto:
dy = (2x - 2) dx ; pak při aplikaci anti-derivačních kritérií máme:
∫dy = ∫ (2x - 2) dx
y = xdva - 2x + C
Použití počáteční podmínky:
2 = (3)dva - 2 (3) + C.
C = -1
Získává se: f (x) = xdva - 2x - 1
- dy / dx = 3xdva - 1 Co prochází bodem (0, 2)
Diferenciální rovnici vyjádříme následovně:
dy = (3xdva - 1) dx ; pak při aplikaci anti-derivačních kritérií máme:
∫dy = ∫ (3xdva - 1) dx
y = x3 - x + C.
Použití počáteční podmínky:
2 = (0)dva - 2 (0) + C.
C = 2
Získává se: f (x) = x3 - x + 2
Navrhovaná cvičení
Cvičení 1
- Najděte primitivní f (x), které splňuje počáteční podmínky:
- f "(x) = x; f '(3) = 1; f (2) = 5
- f "(x) = x + 1; f '(2) = 2; f (0) = 1
- f "(x) = 1; f '(2) = 3; f (1) = 10
- f "(x) = -x; f '(5) = 1; f (1) = -8
Cvičení 2
- Balón stoupající rychlostí 16 ft / s upustí pytel písku z výšky 64 ft nad úrovní země.
- Definujte čas letu
- Co bude vektor VF když jsem narazil na podlahu?
Cvičení 3
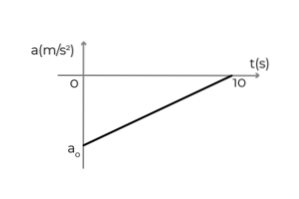
- Obrázek ukazuje graf doby zrychlení automobilu pohybujícího se v kladném směru osy x. Vůz jel konstantní rychlostí 54 km / h, když řidič za 10 sekund zabrzdil. Určit:
- Počáteční zrychlení vozu
- Rychlost vozu při t = 5 s
- Zdvihový objem vozidla během brzdění
Cvičení 4
- Definujte primitivní funkce dané derivacemi a bodem v grafu:
- dy / dx = x, které prochází bodem (-1, 4)
- dy / dx = -xdva + 1 Co prochází bodem (0, 0)
- dy / dx = -x + 1, které prochází bodem (-2, 2)
Reference
- Integrální počet. Neurčitý integrál a integrační metody. Wilson, Velásquez Bastidas. Magdalena University 2014
- Stewart, J. (2001). Výpočet proměnné. Brzy transcendentální. Mexiko: Thomson Learning.
- Jiménez, R. (2011). Matematika VI. Integrální počet. Mexiko: Pearson Education.
- Fyzika I. Mc Graw Hill



Zatím žádné komentáře