
Příklady sférických souřadnic a řešená cvičení

The sférické souřadnice jsou bodový lokalizační systém v trojrozměrném prostoru skládající se z radiální souřadnice a dvou úhlových souřadnic zvaných polární souřadnice a azimutová souřadnice.
Obrázek 1, který vidíme níže, ukazuje sférické souřadnice (r, θ, φ) bodu M. Tyto souřadnice se vztahují k ortogonální soustavě kartézských os X, Y, Z počátku O.
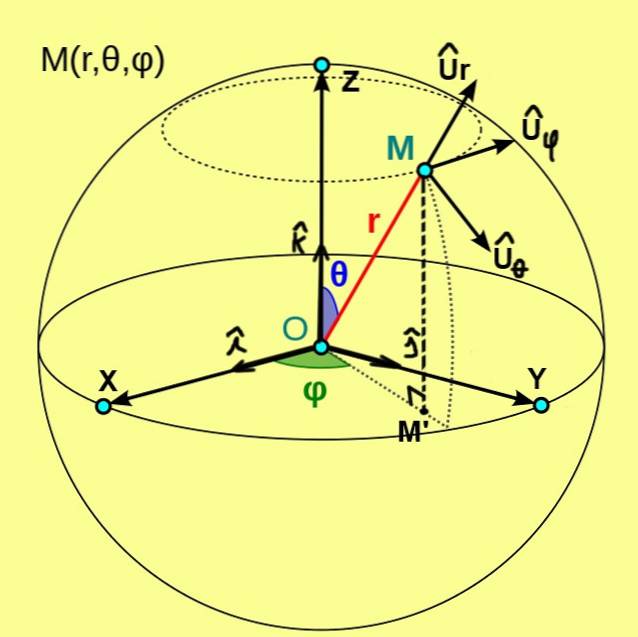
V tomto případě je souřadnice r bodu M vzdálenost od tohoto bodu k počátku O. Polární souřadnice θ představuje úhel mezi kladnou poloosou Z a poloměrem vektoru OM. Zatímco azimutální souřadnice φ je úhel mezi kladnou poloosou X a poloměrem vektoru OM ', kde M' je ortogonální projekce M na rovinu XY.
Radiální souřadnice r má pouze kladné hodnoty, ale pokud je bod umístěn v počátku, pak r = 0. Polární souřadnice θ bere jako minimální hodnotu 0 ° pro body umístěné na kladné poloosě Z a maximální hodnota 180 ° pro body je umístěna na záporné polořadovce Z. Nakonec azimutální souřadnice φ bere jako minimální hodnotu 0 ° a maximální výška 360 °.
0 ≤ r < ∞
0 ≤ θ ≤ 180 °
0 ≤ φ < 360º
Rejstřík článků
- 1 Změna souřadnic
- 1.1 Vektorová základna ve sférických souřadnicích
- 1.2 Přímkové a objemové prvky ve sférických souřadnicích
- 2 Vztah k zeměpisným souřadnicím
- 2.1 Změna vzorců z geografických na sférické
- 3 příklady
- 3.1 Příklad 1
- 3.2 Příklad 2
- 4 cvičení
- 4.1 Cvičení 1
- 4.2 Cvičení 2
- 5 Reference
Změna souřadnic
Vzorce, které umožňují získání kartézských souřadnic (x, y, z) bodu M, budou uvedeny níže za předpokladu, že jsou známy sférické souřadnice stejného bodu (r, θ, φ):
x = r Sen (θ) Cos (φ)
y = r Sen (θ) Sen (φ)
z = r Cos (θ)
Stejným způsobem je užitečné najít vztahy, které mají jít od kartézských souřadnic (x, y, z) daného bodu ke sférickým souřadnicím uvedeného bodu:
r = √ (x ^ 2 + y ^ 2 + z ^ 2)
θ = Arctan (√ (x ^ 2 + y ^ 2) / z)
φ = Arctan (y / x)
Vektorový základ ve sférických souřadnicích
Ze sférických souřadnic je definován ortonormální základ základních vektorů, které jsou označeny Ur, Uθ, Uφ. Obrázek 1 ukazuje tyto tři jednotkové vektory, které mají následující charakteristiky:
- Ur je jednotkový vektor tečny k radiální přímce θ = ctte a φ = ctte;
- Uθ je jednotkový vektor tangenta k oblouku φ = ctte ar = ctte;
- Uφ je jednotkový vektor tangenta k oblouku r = ctte a θ = ctte.
Přímkové a objemové prvky ve sférických souřadnicích
Vektor polohy bodu v prostoru ve sférických souřadnicích je napsán takto:
r = r Ur
Ale nekonečně malá variace nebo posunutí bodu v trojrozměrném prostoru, v těchto souřadnicích, je vyjádřena následujícím vektorovým vztahem:
dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ
Nakonec je nekonečně malý objem dV ve sférických souřadnicích napsán takto:
dV = r ^ 2 Sen (θ) dr dθ dφ
Tyto vztahy jsou velmi užitečné pro výpočet liniových a objemových integrálů ve fyzických situacích, které mají sférickou symetrii..
Vztah k zeměpisným souřadnicím
Geografickými souřadnicemi se rozumí ty, které slouží k lokalizaci míst na zemském povrchu. Tento systém používá k lokalizaci polohy na povrchu Země souřadnice zeměpisné šířky a délky..
V geografickém souřadnicovém systému se předpokládá, že zemský povrch je sférický s poloměrem Rt, i když je známo, že je u pólů zploštělý, a uvažuje se o sadě imaginárních čar zvaných rovnoběžky a meridiány.
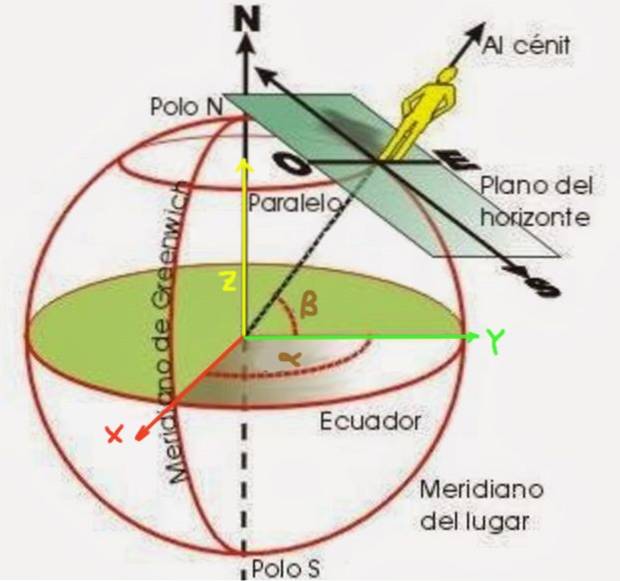
Zeměpisná šířka β je úhel tvořený poloměrem, který začíná od středu Země k bodu, který chcete umístit. Měří se z rovníkové roviny, jak je znázorněno na obrázku 2. Na druhou stranu, délka α je úhel, který poledník bodu, který je umístěn, tvoří vzhledem k nulovému poledníku (známému jako greenwichský poledník).
Zeměpisná šířka může být severní nebo jižní zeměpisná šířka, v závislosti na tom, zda se místo, které lokalizujete, nachází na severní polokouli nebo na jižní polokouli. Podobně může být zeměpisná délka na západ nebo na východ v závislosti na tom, zda je poloha na západ nebo na východ od nultého poledníku..
Vzorce, které se mají změnit z geografického na sférické
K získání těchto vzorců je první věcí vytvořit souřadnicový systém. Rovina XY je zvolena tak, aby se shodovala s rovníkovou rovinou, přičemž kladná poloosa X je rovina, která prochází středem Země a prochází nulovým poledníkem. Osa Y zase prochází poledníkem 90 ° E. Zemský povrch má poloměr Rt.
S tímto souřadným systémem vypadají transformace z geografického na sférický takto:
αEβN → (Rt, θ = 90º-β, φ = α)
αOβN → (Rt, θ = 90º-β, φ = 360º-α)
αEβS → (Rt, θ = 90 ° + β, φ = α)
αOβS → (Rt, θ = 90 ° + β, φ = 360 °-α)
Příklady
Příklad 1
Zeměpisné souřadnice Palma de Mallorca (Španělsko) jsou:
Východní délka 38,847 ° a severní šířka 39,570 °. K určení sférických souřadnic odpovídajících Palma de Mallorca se použije první ze vzorců vzorců v předchozí části:
38 847 ° E 39 570 ° N → (r = 6371 km, θ = 90 ° - 39 570 °, φ = 38 847 °)
Sférické souřadnice jsou tedy:
Palma de Mallorca: (r = 6371 km, θ = 50,43 °, φ = 38,85 °)
V předchozí odpovědi jsme vzali r rovnající se průměrnému poloměru Země.
Příklad 2
S vědomím, že Falklandské ostrovy (Malvíny) mají zeměpisné souřadnice 59 ° O 51,75 ° jižní šířky, určete odpovídající polární souřadnice. Pamatujte, že osa X jde od středu Země k poledníku 0 ° a v rovníkové rovině; osa Y také v rovníkové rovině a procházející 90 ° západním poledníkem; nakonec osa Z na ose rotace Země ve směru jih-sever.
K nalezení odpovídajících sférických souřadnic pak použijeme vzorce uvedené v předchozí části:
59 ° O 51,75 ° S → (r = 6371 km, θ = 90 ° + 51,75 °, φ = 360 ° -59 °), což je
Falklandy: (r = 6371 km, θ = 141,75 °, φ = 301 °)
Výcvik
Cvičení 1
Najděte kartézské souřadnice Palma de Mallorca v kartézském referenčním systému XYZ zobrazeném na obrázku 2.
Řešení: Dříve v příkladu 1 byly sférické souřadnice získány od zeměpisných souřadnic Palma de Mallorca. Výše uvedené vzorce lze tedy použít k přechodu ze sférického na kartézský:
x = 6371 km Sen (50,43 °) Cos (38,85 °)
y = 6371 km Sen (50,43 °) Sen (38,85 °)
z = 6371 km Cos (50,43 °)
Provedením odpovídajících výpočtů máme:
Palma de Mallorca: (x = 3825 km, y = 3081 km, z = 4059)
Cvičení 2
Najděte kartézské souřadnice Falklandských ostrovů v kartézském referenčním systému XYZ zobrazeném na obrázku 2.
Řešení: Dříve v příkladu 2 byly sférické souřadnice získány od zeměpisných souřadnic Falklandských ostrovů. Výše uvedené vzorce lze tedy použít k přechodu ze sférického na kartézský:
x = 6371 km Sen (141,75 °) Cos (301 °)
y = 6371 km Sen (141,75 °) Sen (301 °)
z = 6371 km Cos (141,75 °)
Provedením příslušných výpočtů získáme:
Falklandské ostrovy: (x = 2031 km, y = -3381 km, z = -5003)
Reference
- Arfken G a Weber H. (2012). Matematické metody pro fyziky. Komplexní průvodce. 7. vydání. Akademický tisk. ISBN 978-0-12-384654-9
- Výpočet cc. Vyřešené problémy válcových a sférických souřadnic. Obnoveno z: Calclo.cc
- Astronomický workshop. Zeměpisná šířka a zeměpisná délka. Obnoveno z: tarifamates.blogspot.com/
- Weisstein, Eric W. "Sférické souřadnice." Z webu MathWorld-A Wolfram. Obnoveno z: mathworld.wolfram.com
- wikipedia. Sférický souřadný systém. Obnoveno z: en.wikipedia.com
- wikipedia. Vektorová pole ve válcových a sférických souřadnicích. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře