Co je Edge of a Cube?

The hrana kostky Je to jeho hrana: je to čára, která spojuje dva vrcholy nebo rohy. Okraj je čára, kde se protínají dvě plochy geometrického útvaru.

Výše uvedená definice je obecná a platí pro jakýkoli geometrický útvar, nejen pro krychli. Je-li to plochá postava, okraje odpovídají stranám uvedené postavy.

Rovnoběžník se nazývá geometrický útvar se šesti tvářemi ve formě rovnoběžníků, z nichž ty opačné jsou stejné a rovnoběžné..

V konkrétním případě, kdy jsou plochy čtvercové, se rovnoběžnostěn nazývá krychle nebo šestihran, což je postava, která se považuje za pravidelný mnohostěn..

Způsoby identifikace hran krychle

Pro lepší ilustraci lze pomocí běžných předmětů přesně určit, jaké jsou hrany krychle.

1- Sestavení papírové kostky

Pokud se podíváte na to, jak je postavena papírová nebo lepenková kostka, uvidíte, jaké jsou její hrany. Začnete nakreslením kříže, jako je ten na obrázku, a uvnitř označíte určité čáry.

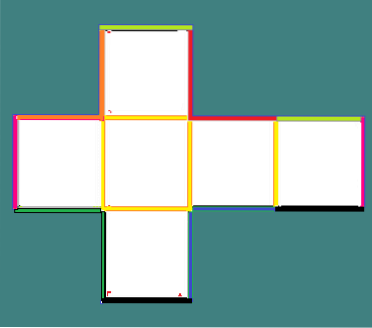
Každá ze žlutých čar představuje záhyb, který bude hranou krychle (hrana).

Podobně každá dvojice čar, které mají stejnou barvu, vytvoří hranu, když se spojí. Celkově má ​​kostka 12 hran.

2- Kreslení krychle

Dalším způsobem, jak zjistit, jaké jsou hrany krychle, je sledovat, jak je nakreslena. Začneme nakreslením čtverce se stranou L; každá strana čtverce je hranou krychle.

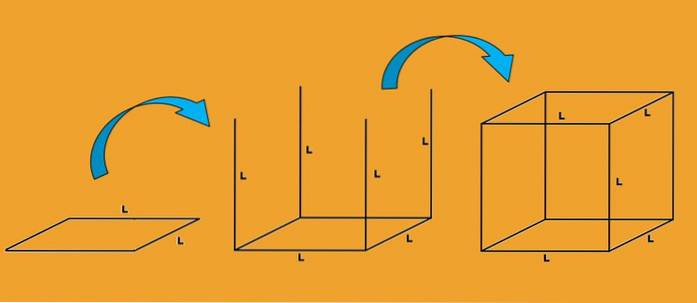
Potom jsou z každého vrcholu nakresleny čtyři svislé čáry a délka každé z těchto čar je L. Každá čára je také hranou krychle.

Nakonec je nakreslen další čtverec se stranou L, takže jeho vrcholy se shodují s koncem hran nakreslených v předchozím kroku. Každá ze stran tohoto nového čtverce je hranou krychle.

3- Rubikova kostka

Pro ilustraci geometrické definice, která byla uvedena na začátku, se můžete podívat na Rubikovu kostku.

Každá tvář má jinou barvu. Okraje jsou reprezentovány čarou, kde se protínají tváře s různými barvami.

Eulerova věta

Eulerova věta pro mnohostěn říká, že vzhledem k mnohostěnu se počet ploch C plus počet vrcholů V rovná počtu hran A plus 2. To znamená, že C + V = A + 2.

Na předchozích obrázcích vidíte, že krychle má 6 ploch, 8 vrcholů a 12 hran. Proto splňuje Eulerovu větu pro mnohostěny, protože 6 + 8 = 12 + 2.

Znát délku hrany krychle je velmi užitečné. Pokud je známa délka hrany, je známa délka všech jejích hran, se kterými lze získat určitá data krychle, například její objem.

Objem krychle je definován jako L³, kde L je délka jejích hran. Proto, abychom poznali objem krychle, je nutné znát pouze hodnotu L.

Reference

1. Guibert, A., Lebeaume, J., & Mousset, R. (1993). Geometrické aktivity pro kojence a základní vzdělávání: pro kojence a základní vzdělávání. Vydání Narcea.
2. Itzcovich, H. (2002). Studium postav a geometrických těles: aktivity pro první roky školní docházky. Knihy Noveduc.
3. Rendon, A. (2004). AKTIVITY SEZNAM 3 2. VYSOKÁ ŠKOLA. Redakční Tebar.
4. Schmidt, R. (1993). Popisná geometrie se stereoskopickými obrazci. Reverte.
5. Spektrum (vyd.). (2013). Geometrie, stupeň 5. Publikace Carson-Dellosa.