Jaký je rozdíl mezi cestou a posunem?

The hlavní rozdíl mezi trajektorií a posunem je to, že druhý je vzdálenost a směr uražený objektem, zatímco první je cesta nebo tvar, který má pohyb daného objektu.

Chcete-li však jasněji vidět rozdíly mezi posunem a trajektorií, je lepší specifikovat jeho konceptualizaci pomocí příkladů, které umožňují lepší pochopení obou termínů..

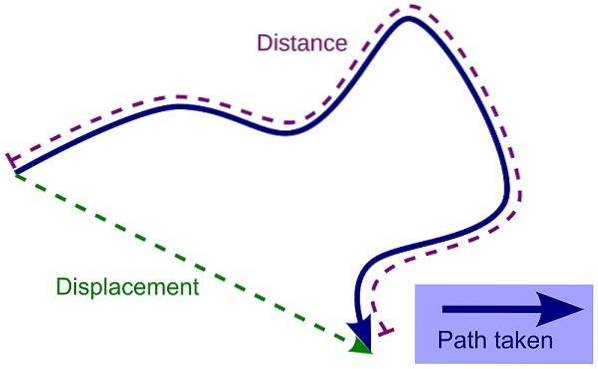
Přemístění

Chápe se jako vzdálenost a směr uražený objektem, přičemž se bere v úvahu jeho počáteční poloha a konečná poloha, vždy v přímce. Pro jeho výpočet, protože jde o vektorovou velikost, se používá měření délky známé jako centimetry, metry nebo kilometry..

Vzorec pro výpočet posunutí je definován takto:

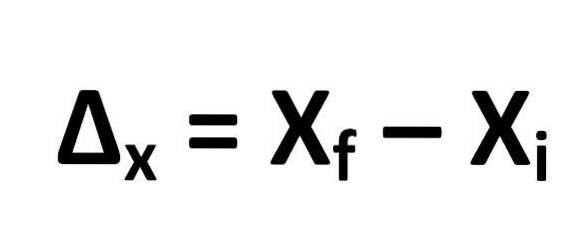
Z čehož vyplývá, že:

• Δ_X = výtlak
• X_F = konečná poloha objektu
• X_i = počáteční poloha objektu

Příklad posunutí

1- Pokud je skupina dětí na začátku trasy, jejíž počáteční poloha je 50 m, pohybující se po přímce, určete posunutí v každém z bodů X_F . 

• X_F = 120 m
• X_F = 90 m
• X_F = 60 m
• X_F = 40 m

2 - Data problému se získají nahrazením hodnot X_dva a X₁ v ofsetovém vzorci:

• Δ_X = ?
• X_i = 50 m
• Δ_X = X_F - X_i
• Δ_X = 120 m - 50 m = 70 m

3- V tomto prvním přístupu říkáme, že Δ_X se rovná 120 m, což odpovídá první hodnotě, kterou najdeme u X_F, minus 50 m, což je hodnota X_i, Výsledkem je 70 m, to znamená, že při dosažení ujetých 120 m byl posun 70 m doprava.

4- Pokračujeme v řešení stejným způsobem pro hodnoty b, c a d

• Δ_X = 90 m - 50 m = 40 m
• Δ_X = 60 m - 50 m = 10 m
• Δ_X = 40 m - 50 m = - 10 m

V tomto případě nám posun dal záporné, to znamená, že konečná poloha je v opačném směru než počáteční poloha.

Trajektorie

Je to trasa nebo čára určená objektem během jeho pohybu a jeho vyhodnocení v mezinárodním systému, obecně přijímá geometrické tvary, jako je čára, parabola, kruh nebo elipsa). Identifikuje se pomocí imaginární čáry a protože se jedná o skalární veličinu, měří se v metrech.

Je třeba poznamenat, že pro výpočet trajektorie musíme vědět, zda je tělo v klidu nebo v pohybu, to znamená, že je podrobeno referenčnímu systému, který vybereme.

Rovnice pro výpočet trajektorie objektu v mezinárodním systému je dána vztahem:

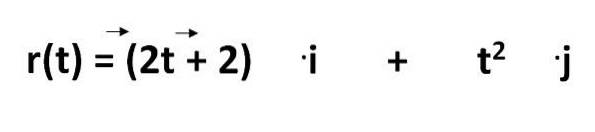
Z toho musíme:

• r (t) = je rovnice cesty
• 2t - 2 at^dva = představují souřadnice jako funkci času
• ^.já a ^.j = jsou jednotkové vektory

Abychom porozuměli výpočtu cesty, kterou urazil objekt, vytvoříme následující příklad:

• Vypočítejte rovnici trajektorií následujících polohových vektorů:

1. r (t) = (2t + 7) ^.i + t^{dva .}j
2. r (t) = (t - 2) ^.i + 2t ^.j

První krok: Protože rovnice cesty je funkcí X, definujte hodnoty X a Y v každém z navrhovaných vektorů:

1- Vyřešte první vektor polohy:

• r (t) = (2t + 7) ^.i + t^{dva .}j

2- Ty = f (x), kde X je dáno obsahem jednotkového vektoru ^.i a Y jsou dány obsahem jednotkového vektoru ^.j:

• X = 2t + 7
• Y = t^dva

3- y = f (x), to znamená, že čas není součástí výrazu, proto ho musíme vyřešit, máme:

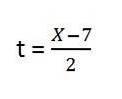
4- Nahradíme vůli v Y. Zbývá:

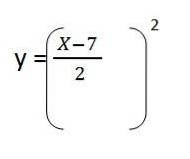
5- Vyřešíme obsah závorek a máme rovnici výsledné cesty pro první jednotkový vektor:

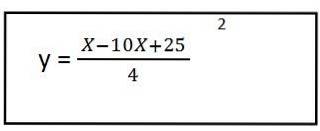
Jak vidíme, dalo nám to rovnici druhého stupně, to znamená, že trajektorie má tvar paraboly.

Druhý krok: Stejným způsobem postupujeme při výpočtu trajektorie vektoru druhé jednotky

r (t) = (t - 2) ^.i + 2t ^.j

• X = t - 2
• Y = 2t

2 - Po krocích, které jsme viděli dříve y = f (x), musíme vyčistit čas, protože není součástí výrazu, zbývá nám:

• t = X + 2

3- Nahradíme vůli v Y, zbývající:

• y = 2 (X + 2)

4- Vyřešením závorek máme rovnici výsledné trajektorie pro vektor druhé jednotky:

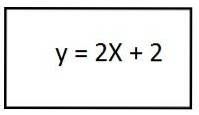
V tomto postupu byla výsledkem přímka, která nám říká, že trajektorie má přímočarý tvar.

Jakmile pochopíme pojmy posunutí a trajektorie, můžeme odvodit zbytek rozdílů, které mezi oběma pojmy existují.

Více rozdílů mezi posunem a trajektorií

Přemístění

• Je to vzdálenost a směr uražený objektem s přihlédnutím k jeho počáteční poloze a jeho konečné poloze.
• Vždy se to děje v přímce.
• Rozpozná se pomocí šipky.
• Použijte měření délky (centimetr, metr, kilometr).
• Je to vektorová veličina.
• Vezměte v úvahu směr jízdy (vpravo nebo vlevo)
• Nezohledňuje čas strávený během prohlídky.
• Nezáleží na referenčním systému.
• Když je počáteční bod stejný počáteční bod, posun je nulový.
• Modul se musí shodovat s prostorem pro cestování, pokud je cesta přímka a nedochází ke změnám ve směru, který je třeba sledovat.
• Modul má tendenci se zvyšovat nebo snižovat, jak dochází k pohybu, přičemž je třeba mít na paměti trajektorii.

Trajektorie

Je to cesta nebo čára určená objektem během jeho pohybu. Přijímá geometrické tvary (přímé, parabolické, kruhové nebo eliptické).

• Představuje to imaginární čára.
• Měří se v metrech.
• Je to skalární veličina.
• Nezohledňuje směr jízdy.
• Zvažte čas strávený během prohlídky.
• Závisí na referenčním systému.
• Pokud je počáteční bod nebo počáteční poloha stejná jako konečná poloha, je trajektorie dána ujetou vzdáleností.
• Hodnota trajektorie se shoduje s modulem vektoru posunutí, pokud je výsledná trajektorie přímka, ale nedochází ke změnám ve směru, který je třeba sledovat.
• Vždy se zvyšuje, když se tělo pohybuje, bez ohledu na trajektorii.

Reference

1. Alvarado, N. (1972) Fyzický. První rok vědy. Redakční Fotoprin C.A. Venezuela.
2. Fernández, M; Fidalgo, J. (2016). Fyzika a chemie 1. bakalář. Edice Paraninfo, S.A. Španělsko.
3. Guatemalský institut rozhlasového vzdělávání. (2011) Základní fyzika. První semestr skupiny Zaculeu. Guatemala.
4. Fernández, P. (2014) Vědeckotechnická oblast. Edice Paraninfo. S.A. Španělsko.
5. Fisica Lab (2015) Vektorové posunutí. Obnoveno z: fisicalab.com.
6. Příklady posunutí. (2013). Obnoveno z: examplesde.com.
7. Projekt Living Room Home (2014) Co je vysídlení? Obnoveno z: salonhogar.net.
8. Fyzikální laboratoř (2015) Pojem trajektorie a polohové rovnice. Obnoveno z: fisicalab.com.