
Rozdíl vzorců kostek, rovnice, příklady, cvičení
The rozdíl kostek je binomické algebraické vyjádření tvaru a3 - b3, kde členy a a b mohou být reálná čísla nebo algebraické výrazy různých typů. Příklad rozdílu kostek je: 8 - x3, protože 8 lze zapsat jako 23.
Geometricky můžeme uvažovat o velké krychli se stranou a, od které se odečte malá kostka se stranou b, jak je znázorněno na obrázku 1:
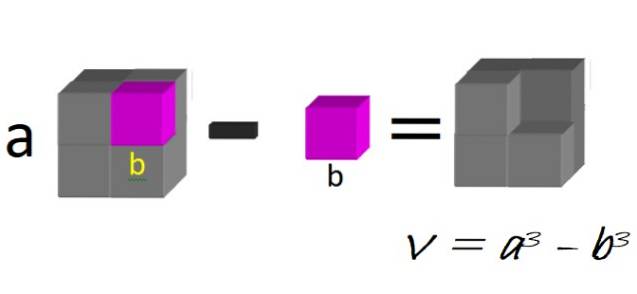
Objem výsledného obrázku je přesně rozdíl kostek:
V = a3 - b3
Chcete-li najít alternativní výraz, pozorujeme, že tento údaj lze rozložit na tři hranoly, jak je znázorněno níže:
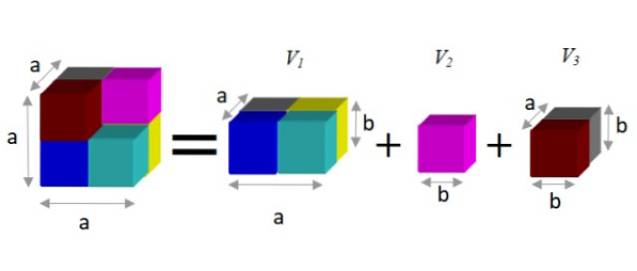
Hranol má objem daný produktem jeho tří dimenzí: šířka x výška x hloubka. Tímto způsobem je výsledný objem:
V = a3 - b3 = adva.b + b3 + a. bdva
Faktor b je to společné pro pravici. Na výše uvedeném obrázku dále platí, že:
b = (a / 2) ⇒ a = b + b
Lze tedy říci, že: b = a - b. Tím pádem:
na3 - b3 = b (adva + bdva +a.b) = (a-b) (a. b)dva + a.b + bdva)
Tento způsob vyjádření rozdílu kostek se ukáže jako velmi užitečný v mnoha aplikacích a byl by získán stejným způsobem, i kdyby se strana chybějící krychle v rohu lišila od b = a / 2.
Všimněte si, že druhá závorkavypadá hodně jako pozoruhodný součin druhé mocniny součtu, ale křížový termín není vynásoben 2. Čtenář může vyvinout pravou stranu, aby ověřil, že je skutečně získán na3 - b3.
Rejstřík článků
- 1 Příklady
- 1.1 Faktorování rozdílu kostek
- 2 Cvičení vyřešeno
- 2.1 Cvičení 1
- 2.2 Cvičení 2
- 3 Odkazy
Příklady
Existuje několik rozdílů kostek:
1 - m6
na6b3 - 8z12Y6
(1/125) .x6 - 27 a9
Pojďme analyzovat každého z nich. V prvním příkladu lze 1 zapsat jako 1 = 13 a výraz m6 zůstává: (mdva)3. Oba výrazy jsou dokonalé kostky, proto se liší:
1 - m6 = 13 - (mdva)3
Ve druhém příkladu jsou termíny přepsány:
na6b3 = (advab)3
8z12Y6 = 23 (z4)3 (Ydva)3 = (2z4Ydva)3
Rozdíl těchto kostek je: (advab)3 - (2z4Ydva)3.
Nakonec zlomek (1/125) je (1/53), X6 = (xdva)3, 27 = 33 a a9 = (a3)3. Nahrazením toho všeho v původním výrazu získáte:
(1/125) .x6 - 27 let9 = [(1/5) (xdva)]3 - (3r3)3
Faktorování rozdílu kostek
Faktorování rozdílu kostek zjednodušuje mnoho algebraických operací. K tomu stačí použít vzorec odvozený výše:

Nyní postup pro použití tohoto vzorce sestává ze tří kroků:
- Nejprve se získá kořen krychle každé z podmínek rozdílu.
- Poté jsou vytvořeny binomické a trinomické, které se objevují na pravé straně vzorce.
- Nakonec jsou binomické a trinomiální substituovány, aby se dosáhlo konečné faktorizace.
Pojďme si ilustrovat použití těchto kroků u každého z výše uvedených příkladů rozdílu v krychli a získat tak jeho faktorovaný ekvivalent.
Příklad 1
Faktorový výraz 1 - m6 podle uvedených kroků. Začínáme přepisováním výrazu na 1 - m6 = 13 - (mdva)3 extrahovat příslušné kořeny krychle každého termínu:


Dále jsou konstruovány binomické a trinomické:
a = 1
b = mdva
Pak:
a - b = 1 - mdva
(nadva +a.b + bdva) = 1dva + 1.mdva + (mdva)dva = 1 + mdva + m4
Nakonec je ve vzorci a nahrazen3 - b3 = (a-b) (adva +a.b + bdva):
1 - m6 = (1 - mdva) (1 + m.)dva + m4)
Příklad 2
Faktorizovat:
na6b3 -8z12Y6 = (advab)3 - (2z4Ydva)3
Jelikož se jedná o dokonalé kostky, kořeny krychle jsou okamžité: advab a 2z4Ydva, z toho tedy vyplývá, že:
- Binomický: advab - 2z4Ydva
- Trinomial: (advab)dva + nadvab. 2z4Ydva + (nadvab + 2z4Ydva)dva
A nyní je vytvořena požadovaná faktorizace:
na6b3 -8z12Y6 = (advab - 2z4Ydva). [(nadvab)dva + nadvab. 2z4Ydva + (nadvab + 2z4Ydva)dva] =
= (advab - 2z4Ydva). [na4bdva + 2. místodvaB z4Ydva + (nadvab + 2z4Ydva)dva]
Faktoring je v zásadě připraven, ale každý termín je často nutné zjednodušit. Poté vyvineme pozoruhodný produkt - čtverec součtu - který se objeví na konci a poté přidáme podobné výrazy. Pamatujte, že čtverec součtu je:
(x + y)dva = xdva + 2xy + adva
Pozoruhodný produkt napravo je vyvíjen takto:
(nadvab + 2z4Ydva)dva = a4bdva + 4. místodvaB z4Ydva + 4z8Y4
Nahrazení expanze získané při faktorizaci rozdílu kostek:
na6b3 -8z12Y6 = (advab - 2z4Ydva). [na4bdva + 2. místodvaB z4Ydva + na4bdva + 4. místodvaB z4Ydva + 4z8Y4] =
Nakonec seskupením podobných výrazů a rozčleněním numerických koeficientů, které jsou všechny sudé, získáme:
(nadvab - 2z4Ydva). [2a4bdva + 6.dvaB z4Ydva + 4z8Y4] = 2 (advab - 2z4Ydva). [na4bdva + 3. místodvaB z4Ydva + 2z8Y4]
Příklad 3
Faktor (1/125) .x6 - 27 let9 je to mnohem jednodušší než v předchozím případě. Nejprve jsou identifikovány ekvivalenty a a b:
a = (1/5) xdva
b = 3 roky3
Pak jsou přímo substituovány ve vzorci:
(1/125) .x6 - 27 let9 = [(1/5) xdva - 3 roky3]. [(1/25) x4 + (3/5) xdvaY3 + 9 let6]
Cvičení vyřešeno
Rozdíl kostek má, jak jsme již řekli, řadu aplikací v algebře. Podívejme se na některé:
Cvičení 1
Vyřešte následující rovnice:
a) x5 - 125 xdva = 0
b) 64 - 729 x3 = 0
Řešení
Nejprve je rovnice zapracována tímto způsobem:
Xdva (X3 - 125) = 0
Protože 125 je dokonalá krychle, jsou závorky psány jako rozdíl kostek:
Xdva . (X3 - 53) = 0
První řešení je x = 0, ale najdeme více, pokud uděláme x3 - 53 = 0, pak:
X3 = 53 → x = 5
Řešení b
Levá strana rovnice je přepsána jako 64 - 729 x3 = 43 - (9x)3. Proto:
43 - (9x)3 = 0
Protože exponent je stejný:
9x = 4 → x = 9/4
Cvičení 2
Zvažte výraz:
(x + y)3 - (x - y)3
Řešení
Tento výraz je rozdílem kostek, pokud si ve faktoringovém vzorci všimneme, že:
a = x + y
b = x- y
Nejprve je sestrojen binomiál:
a - b = x + y - (x- y) = 2y
A teď trinomial:
nadva + a.b + bdva = (x + y)dva + (x + y) (x-y) + (x-y)dva
Byly vyvinuty významné produkty:
(x + y)dva = xdva + 2xy + adva
(x + y) (x-y) = xdva- Ydva
(x- y)dva = xdva - 2xy + adva
Dále musíte nahradit a snížit podobné výrazy:
nadva + a.b + bdva = xdva + 2xy + adva+ Xdva- Ydva+ Xdva - 2xy + adva = 3xdva + Ydva
Výsledkem faktoringu je:
(x + y)3 - (x - y)3 = 2 roky. (3xdva + Ydva)
Reference
- Baldor, A. 1974. Algebra. Redakční Kulturní Venezolana S.A.
- Nadace CK-12. Součet a rozdíl kostek. Obnoveno z: ck12.org.
- Khan Academy. Faktorování rozdílů kostek. Obnoveno z: es.khanacademy.org.
- Matematika je zábava pro pokročilé. Rozdíl dvou kostek. Obnoveno z: mathsisfun.com
- UNAM. Faktorování rozdílu kostek. Obnoveno z: dcb.fi-c.unam.mx.



Zatím žádné komentáře