
Charakteristiky distribuce F a vyřešená cvičení
The distribuce F o Fisher-Snedecor distribuce je ta, která se používá k porovnání odchylek dvou různých nebo nezávislých populací, z nichž každá sleduje normální distribuci.
Distribuce, která následuje po rozptylu sady vzorků z jedné normální populace, je distribuce chí-kvadrát (Χdva) stupně n-1, pokud má každý ze vzorků v sadě n prvků.
Pro porovnání odchylek dvou různých populací je nutné definovat a statistický, to znamená, pomocná náhodná proměnná, která nám umožňuje rozlišit, zda obě populace mají stejnou odchylku.
Uvedená pomocná proměnná může být přímo kvocient rozptylu vzorků každé populace, v takovém případě, pokud je uvedený kvocient blízký jednotě, existují důkazy, že obě populace mají podobné odchylky.
Rejstřík článků
- 1 Statistika F a její teoretické rozdělení
- 1.1 Průměr, režim a rozptyl rozdělení F
- 2 Manipulace s F distribucí
- 2.1 Tabulky distribuce F.
- 2.2 Software pro distribuci F.
- 3 Vyřešená cvičení
- 3.1 Cvičení 1
- 3.2 Cvičení 2
- 4 Odkazy
Statistika F a její teoretické rozdělení
Statistika náhodných proměnných F nebo F navržená Ronaldem Fisherem (1890 - 1962) je nejčastěji používanou pro srovnání rozptylů dvou populací a je definována následovně:
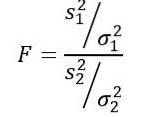
Být sdva rozptyl vzorku a σdva populační rozptyl. K rozlišení každé ze dvou populačních skupin se používají dolní indexy 1 a 2..
Je známo, že distribuce chí-kvadrát s (n-1) stupni volnosti je ta, která následuje za pomocnou (nebo statistickou) proměnnou definovanou níže:
Xdva = (n-1) sdva / σdva.
Statistika F proto sleduje teoretické rozdělení dané následujícím vzorcem:
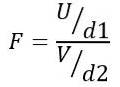
Bytost NEBO distribuce chí-kvadrát s d1 = n1 - 1 stupně volnosti pro populaci 1 a PROTI distribuce chí-kvadrát s d2 = n2 - 1 stupně volnosti pro obyvatelstvo 2.
Takto definovaný kvocient je nové rozdělení pravděpodobnosti, známé jako F distribuce s d1 stupně volnosti v čitateli a d2 stupně volnosti ve jmenovateli.
Průměr, režim a rozptyl rozdělení F
Polovina
Průměr distribuce F se vypočítá takto:
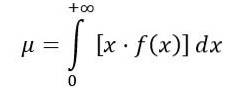
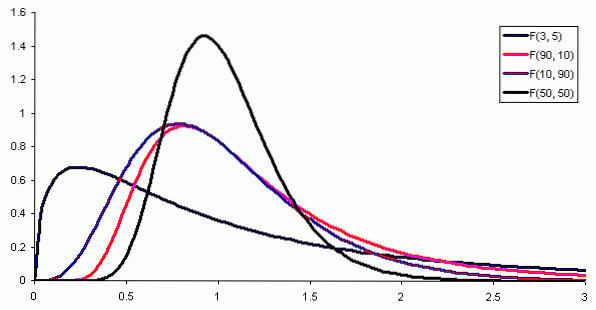
Kde f (x) je hustota pravděpodobnosti distribuce F, která je znázorněna na obrázku 1 pro různé kombinace parametrů nebo stupňů volnosti.
Můžeme zapsat hustotu pravděpodobnosti f (x) jako funkci funkce Γ (funkce gama):
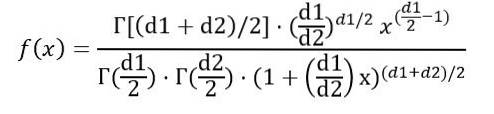
Po provedení výše uvedeného integrálu se dospělo k závěru, že průměr F distribuce se stupni volnosti (d1, d2) je:
μ = d2 / (d2 - 2) s d2> 2
Je třeba poznamenat, že kupodivu průměr nezávisí na stupních volnosti d1 čitatele.
móda
Na druhou stranu režim závisí na d1 a d2 a je dán vztahem:
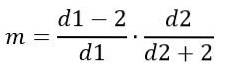
Pro d1> 2.
Rozptyl distribuce F.
Rozptyl σdva distribuce F se počítá z integrálu:
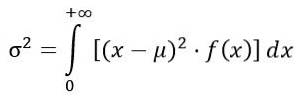
Získání:
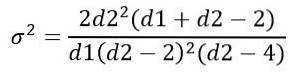
Manipulace s F distribucí
Stejně jako ostatní kontinuální distribuce pravděpodobnosti, které zahrnují komplikované funkce, se zpracování distribuce F provádí pomocí tabulek nebo softwaru..
Distribuční tabulky F
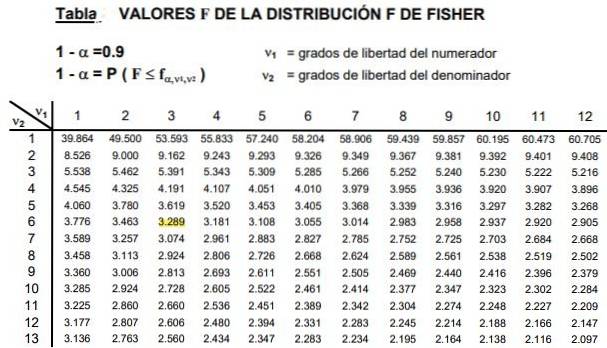
Tabulky zahrnují dva parametry nebo stupně volnosti distribuce F, sloupec označuje stupeň volnosti čitatele a řádek stupeň volnosti jmenovatele.
Obrázek 2 ukazuje řez tabulkou distribuce F pro případ a úroveň významnosti 10%, to je α = 0,1. Hodnota F je zvýrazněna, když d1 = 3 a d2 = 6 s úroveň spolehlivosti 1- α = 0,9, což je 90%.
Software pro distribuci F.
Pokud jde o software, který zpracovává distribuci F, existuje velká rozmanitost, například z tabulek Vynikat na specializované balíčky jako minitab, SPSS Y R abychom jmenovali některé z nejznámějších.
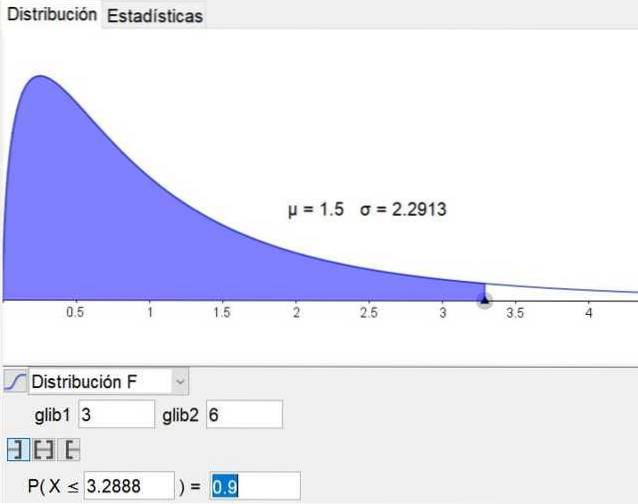
Je pozoruhodné, že software pro geometrii a matematiku geogebra má statistický nástroj, který zahrnuje hlavní rozdělení, včetně rozdělení F. Obrázek 3 ukazuje rozdělení F pro případ d1 = 3 a d2 = 6 s úroveň spolehlivosti 90%.
Vyřešená cvičení
Cvičení 1
Zvažte dva vzorky populací, které mají stejnou populační rozptyl. Pokud má vzorek 1 velikost n1 = 5 a vzorek 2 má velikost n2 = 10, určete teoretickou pravděpodobnost, že podíl jejich příslušných odchylek je menší nebo roven 2.
Řešení
Je třeba si uvědomit, že statistika F je definována jako:
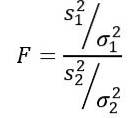
Je nám ale řečeno, že populační odchylky jsou stejné, takže pro toto cvičení platí následující:
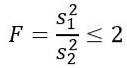
Jelikož chceme znát teoretickou pravděpodobnost, že tento kvocient rozptylu vzorků je menší nebo roven 2, potřebujeme znát oblast pod F distribucí mezi 0 a 2, kterou lze získat pomocí tabulek nebo softwaru. K tomu je třeba vzít v úvahu, že požadované rozdělení F má d1 = n1 - 1 = 5 - 1 = 4 a d2 = n2 - 1 = 10 - 1 = 9, tj. Rozdělení F se stupni volnosti ( 4, 9).
Pomocí statistického nástroje geogebra Bylo zjištěno, že tato oblast je 0,82, takže se dospělo k závěru, že pravděpodobnost, že kvocient rozptylu vzorku je menší nebo roven 2, je 82%.
Cvičení dva
U tenkých plechů existují dva výrobní procesy. Variabilita tloušťky by měla být co nejnižší. Z každého procesu je odebráno 21 vzorků. Vzorek z procesu A má standardní odchylku 1,96 mikronu, zatímco vzorek z procesu B má standardní odchylku 2,13 mikronu. Který z procesů má nejmenší variabilitu? Použijte úroveň odmítnutí 5%.
Řešení
Data jsou následující: Sb = 2,13 s nb = 21; Sa = 1,96 s na = 21. To znamená, že musíme pracovat s F distribucí (20, 20) stupňů volnosti.
Z nulové hypotézy vyplývá, že populační varianta obou procesů je identická, tj. Σa ^ 2 / σb ^ 2 = 1. Alternativní hypotéza by znamenala různé populační odchylky.
Poté, za předpokladu identických populačních odchylek, je vypočítaná statistika F definována jako: Fc = (Sb / Sa) ^ 2.
Protože úroveň odmítnutí byla brána jako α = 0,05, pak α / 2 = 0,025
Distribuce F (0,025; 20,20) = 0,406, zatímco F (0,975; 20,20) = 2,46.
Nulová hypotéza bude tedy pravdivá, pokud vypočtené F splňuje: 0,406≤Fc≤2,46. Jinak je nulová hypotéza odmítnuta.
Protože Fc = (2,13 / 1,96) ^ 2 = 1,18, došlo se k závěru, že statistika Fc je v rozsahu přijatelnosti nulové hypotézy s jistotou 95%. Jinými slovy, s 95% jistotou mají oba výrobní procesy stejnou populační odchylku..
Reference
- F Test nezávislosti. Obnoveno z: saylordotorg.github.io.
- Med Wave. Statistiky aplikované na vědy o zdraví: test F. Citováno z: medwave.cl.
- Pravděpodobnosti a statistiky. Distribuce F. Obnoveno z: probayestadistica.com.
- Triola, M. 2012. Základní statistiky. 11. Edice. Addison Wesley.
- UNAM. Distribuce F. Obnoveno z: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribuce F. Obnoveno z: es.wikipedia.com


Zatím žádné komentáře