
Polynomiální rovnice (s vyřešenými cvičeními)

The polynomiální rovnice Jsou výrokem, který zvyšuje rovnost dvou výrazů nebo členů, přičemž alespoň jeden z výrazů, které tvoří každou stranu rovnosti, jsou polynomy P (x). Tyto rovnice jsou pojmenovány podle stupně jejich proměnných.
Obecně platí, že rovnice je tvrzení, které stanoví rovnost dvou výrazů, kde alespoň v jednom z nich existují neznámé veličiny, které se nazývají proměnné nebo neznámé. I když existuje mnoho typů rovnic, obecně se dělí na dva typy: algebraické a transcendentální..

Polynomiální rovnice obsahují pouze algebraické výrazy, které mohou mít v rovnici jednu nebo více neznámých. Podle exponentu (stupně), který mají, je lze rozdělit na: první stupeň (lineární), druhý stupeň (kvadratický), třetí stupeň (kubický), čtvrtý stupeň (kvartický), stupeň větší nebo rovný pěti a iracionální.
Rejstřík článků
- 1 Funkce
- 2 druhy
- 2.1 První stupeň
- 2.2 Druhá třída
- 2.3 Rozpouštědlo
- 2.4 Hlavní stupeň
- 3 Vyřešená cvičení
- 3.1 První cvičení
- 3.2 Druhé cvičení
- 4 Odkazy
Vlastnosti
Polynomiální rovnice jsou výrazy, které jsou tvořeny rovností mezi dvěma polynomy; tj. konečnými součty násobení mezi neznámými hodnotami (proměnné) a pevnými čísly (koeficienty), kde proměnné mohou mít exponenty a jejich hodnotou může být celé kladné číslo, včetně nuly.
Exponenty určují stupeň nebo typ rovnice. Termín výrazu, který má exponent s nejvyšší hodnotou, bude představovat absolutní stupeň polynomu.
Polynomiální rovnice jsou také známé jako algebraické, jejich koeficienty mohou být reálná nebo komplexní čísla a proměnnými jsou neznámá čísla představovaná písmenem, například: „x“.
Pokud nahradíme hodnotu proměnné „x“ v P (x), výsledek se bude rovnat nule (0), pak se říká, že tato hodnota vyhovuje rovnici (jedná se o řešení) a obecně se nazývá kořen polynomu.
Při vývoji polynomiální rovnice chcete najít všechny kořeny nebo řešení.
Typy
Existuje několik typů polynomiálních rovnic, které se rozlišují podle počtu proměnných a také podle stupně jejich exponentu.
Polynomiální rovnice - kde jeho první člen je polynom, který má jedinou neznámou, vzhledem k tomu, že jeho stupeň může být jakékoli přirozené číslo (n) a druhý člen je nula -, lze vyjádřit následovně:
nan * Xn + nan-1 * Xn-1 +… + A1 * X1 + na0 * X0 = 0
Kde:
- nan, nan-1 již0, jsou skutečné koeficienty (čísla).
- nan se liší od nuly.
- Exponent n je kladné celé číslo, které představuje stupeň rovnice.
- x je proměnná nebo neznámá, která má být prohledána.
Absolutní nebo větší stupeň polynomické rovnice je exponent s nejvyšší hodnotou ze všech, které tvoří polynom; rovnice jsou tedy klasifikovány jako:
První stupeň
Polynomiální rovnice prvního stupně, také známé jako lineární rovnice, jsou rovnice, ve kterých je stupeň (největší exponent) roven 1, polynom má tvar P (x) = 0; a skládá se z lineárního členu a nezávislého členu. Je napsán následovně:
ax + b = 0.
Kde:
- a a b jsou reálná čísla a a ≠ 0.
- ax je lineární člen.
- b je nezávislý termín.
Například rovnice 13x - 18 = 4x.
Chcete-li vyřešit lineární rovnice, všechny výrazy, které obsahují neznámé x, musí být předány jedné straně rovnosti a ty, které ji nemají, se přesunou na druhou stranu, aby ji vyřešily a získaly řešení:
13x - 18 = 4x
13x = 4x + 18
13x - 4x = 18
9x = 18
x = 18 ÷ 9
x = 2.
Daná rovnice má tedy pouze jedno řešení nebo kořen, což je x = 2.
Druhá třída
Polynomiální rovnice druhého stupně, také známé jako kvadratické rovnice, jsou ty, ve kterých je stupeň (největší exponent) roven 2, polynom má tvar P (x) = 0 a skládá se z kvadratického členu, jednoho lineárního a jeden nezávislý. Vyjadřuje se takto:
sekeradva + bx + c = 0.
Kde:
- a, b a c jsou reálná čísla a a ≠ 0.
- sekeradva je kvadratický člen a „a“ je koeficient kvadratického členu.
- bx je lineární člen a „b“ je koeficient lineárního členu.
- c je nezávislý termín.
Solventní
Obecně platí, že řešení tohoto typu rovnic je dáno řešením x z rovnice, a to je následující, které se nazývá resolvent:

Tam, (nardva - 4ac) se nazývá diskriminant rovnice a tento výraz určuje počet řešení, která rovnice může mít:
- Ano Bdva - 4ac) = 0, rovnice bude mít jediné řešení, které je dvojnásobné; to znamená, že bude mít dvě stejná řešení.
- Ano Bdva - 4ac)> 0, rovnice bude mít dvě různá reálná řešení.
- Ano Bdva - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).
Například máme rovnici 4xdva + 10x - 6 = 0, aby se to vyřešilo, nejprve identifikujte pojmy a, b a c a poté jej dosaďte do vzorce:
a = 4
b = 10
c = -6.
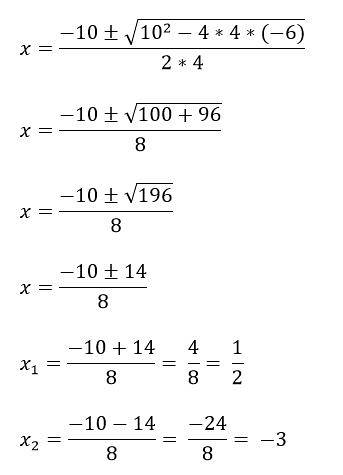
Existují případy, kdy polynomiální rovnice druhého stupně nemají všechny tři termíny, a proto jsou řešeny jiným způsobem:
- V případě, že kvadratické rovnice nemají lineární člen (tj. B = 0), bude rovnice vyjádřena jako axdva + c = 0. Chcete-li to vyřešit, vyřešte pro xdva a odmocniny se aplikují na každého člena, pamatujeme si, že je třeba vzít v úvahu dva možné znaky, které může mít neznámý:
sekeradva + c = 0.
Xdva = - c ÷ a
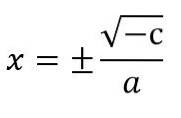
Například 5 xdva - 20 = 0.
5 xdva = 20
Xdva = 20 ÷ 5
x = ± √4
x = ± 2
X1 = 2.
Xdva = -2.
- Pokud kvadratická rovnice nemá nezávislý člen (tj. C = 0), bude rovnice vyjádřena jako axdva + bx = 0. Abychom to vyřešili, musíme vzít společný faktor neznámého x v prvním členu; Protože rovnice je rovna nule, je pravda, že alespoň jeden z faktorů bude roven 0:
sekeradva + bx = 0.
x (ax + b) = 0.
Musíte tedy:
x = 0.
x = -b ÷ a.
Například: máme rovnici 5xdva + 30x = 0. První faktor:
5xdva + 30x = 0
x (5x + 30) = 0.
Jsou generovány dva faktory, které jsou x a (5x + 30). Předpokládá se, že jedna z nich se bude rovnat nule a druhé dostane řešení:
X1 = 0.
5x + 30 = 0
5x = -30
x = -30 ÷ 5
Xdva = -6.
Nejvyšší stupeň
Polynomiální rovnice vyššího stupně jsou rovnice, které jdou od třetího stupně a dále, které lze vyjádřit nebo vyřešit pomocí obecné polynomické rovnice pro libovolný stupeň:
nan * Xn + nan-1 * Xn-1 +… + A1 * X1 + na0 * X0 = 0
Toto se používá, protože rovnice se stupněm větším než dva je výsledkem faktoringu polynomu; to je, to je vyjádřeno jako násobení polynomials stupně jeden nebo vyšší, ale bez skutečných kořenů.
Řešení tohoto typu rovnic je přímé, protože násobení dvou faktorů bude rovno nule, pokud bude některý z faktorů null (0); Proto musí být vyřešena každá z nalezených polynomiálních rovnic, přičemž každý z jejích faktorů je roven nule.
Například máme rovnici x třetího stupně (kubickou)3 + Xdva +4x + 4 = 0. K vyřešení je třeba dodržet následující kroky:
- Výrazy jsou seskupeny:
X3 + Xdva +4x + 4 = 0
(X3 + Xdva ) + (4x + 4) = 0.
- Členové jsou rozloženi, aby získali společný faktor neznáma:
Xdva (x + 1) + 4 (x + 1) = 0
(Xdva + 4)*(x + 1) = 0.
- Tímto způsobem se získají dva faktory, které se musí rovnat nule:
(Xdva + 4) = 0
(x + 1) = 0.
- Je vidět, že faktor (xdva + 4) = 0 nebude mít skutečné řešení, zatímco faktor (x + 1) = 0 bude. Řešení tedy je:
(x + 1) = 0
x = -1.
Vyřešená cvičení
Vyřešte následující rovnice:
První cvičení
(2xdva + 5)*(x - 3)*(1 + x) = 0.
Řešení
V tomto případě je rovnice vyjádřena jako násobení polynomů; to je zohledněno. Aby to bylo možné vyřešit, musí být každý faktor nastaven na nulu:
- 2xdva + 5 = 0, nemá řešení.
- x - 3 = 0
- x = 3.
- 1 + x = 0
- x = - 1.
Daná rovnice má tedy dvě řešení: x = 3 a x = -1.
Druhé cvičení
X4 - 36 = 0.
Řešení
Byl dán polynom, který lze přepsat jako rozdíl čtverců, aby se dospělo k rychlejšímu řešení. Rovnice tedy je:
(Xdva + 6)*(Xdva - 6) = 0.
Pro nalezení řešení rovnic jsou oba faktory nastaveny na nulu:
(Xdva + 6) = 0, nemá řešení.
(Xdva - 6) = 0
Xdva = 6
x = ± √6.
Počáteční rovnice má tedy dvě řešení:
x = √6.
x = - √6.
Reference
- Andres, T. (2010). Tresura matematické olympiády. Springer. New York.
- Angel, A. R. (2007). Elementární algebra. Pearson Education,.
- Baer, R. (2012). Lineární algebra a projektivní geometrie. Courier Corporation.
- Baldor, A. (1941). Algebra. Havana: Kultura.
- Castaño, H. F. (2005). Matematika před kalkulem. University of Medellin.
- Cristóbal Sánchez, M. R. (2000). Olympijský manuál pro matematickou přípravu. Jaume I University.
- Kreemly Pérez, M. L. (1984). Vyšší algebra I.
- Massara, N. C.-L. (devatenáct devadesát pět). Matematika 3.



Zatím žádné komentáře