The chemická aktivační energie (z pohledu kinetických studií) se týká nejmenšího možného množství energie potřebné k zahájení chemické reakce. Podle teorie srážek v chemické kinetice se říká, že všechny molekuly, které jsou v pohybu, mají určité množství kinetické energie.
To znamená, že čím větší je rychlost jeho pohybu, tím větší je velikost jeho kinetické energie. V tomto smyslu nemůže být molekula, která nese rychlý pohyb, sama rozdělena na fragmenty, takže musí dojít ke kolizi mezi ní a jinou molekulou, aby mohla proběhnout chemická reakce..
Když k tomu dojde - když dojde ke kolizi mezi molekulami - zlomek jejich kinetické energie se přemění na energii vibrační. Podobně, pokud je na začátku procesu kinetická energie vysoká, molekuly, které se účastní srážky, budou představovat tak velkou vibraci, že dojde k rozbití některých přítomných chemických vazeb..
Toto rozbití vazeb představuje první krok v transformaci reaktantů na produkty; to znamená při jejich tvorbě. Naopak, pokud bude na začátku tohoto procesu kinetická energie malé velikosti, bude existovat fenomén „odrazu“ molekul, skrz které budou odděleny prakticky neporušené..
Rejstřík článků
Počínaje výše popsaným konceptem srážek mezi molekulami k zahájení chemických reakcí lze říci, že ke vzniku srážky je zapotřebí minimální množství energie..
Pokud je tedy energetická hodnota menší než toto nezbytné minimum, nedojde po srážce k žádným změnám mezi molekulami, což znamená, že když tato energie chybí, zúčastněné druhy zůstanou prakticky neporušené a nedojde k ní. kvůli této havárii.
V tomto pořadí myšlenek se minimální energie potřebná ke změně po srážce mezi molekulami nazývá aktivační energie..
Jinými slovy, molekuly účastnící se srážky musí mít celkové množství kinetické energie stejné nebo větší než aktivační energie, aby mohla chemická reakce proběhnout..
Podobně v mnoha případech molekuly kolidují a vznikají nové druhy zvané aktivovaný komplex, struktura, která se také nazývá „přechodový stav“, protože existuje pouze dočasně..
Je to způsobeno reakčními složkami v důsledku srážky a před tvorbou reakčních produktů.
Aktivovaný komplex zmíněný výše tvoří druh, který má velmi nízkou stabilitu, ale naopak má velkou velikost potenciální energie..
Následující diagram ukazuje transformaci reaktantů na produkty, vyjádřenou jako energie, a upozorňuje, že velikost energie vytvářeného aktivovaného komplexu je podstatně větší než u reaktantů a produktů..
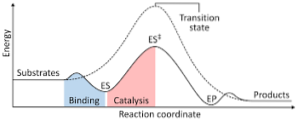
Pokud mají produkty na konci reakce větší stabilitu než reaktivní látky, dochází k uvolňování energie ve formě tepla a dochází k exotermické reakci..
Naopak, mají-li reaktanty větší stabilitu než produkty, znamená to, že reakční směs projevuje absorpci energie ve formě tepla ze svého okolí, což vede k endotermické reakci..
Podobně, pokud dojde k jednomu nebo druhému případu, měl by být sestaven diagram, jako je ten, který byl ukázán dříve, kde je vynesena potenciální energie systému, který reaguje proti postupu nebo postupu reakce..
Tak se získají potenciální energetické změny, ke kterým dochází v průběhu reakce a reaktanty se transformují na produkty..
Aktivační energie chemické reakce úzce souvisí s rychlostní konstantou uvedené reakce a závislost této konstanty na teplotě představuje Arrheniova rovnice:
k = Ae-Ea / RT
V tomto výrazu k představuje rychlostní konstantu reakce (která závisí na teplotě) a parametr NA se nazývá frekvenční faktor a je mírou frekvence srážek mezi molekulami.
Pro jeho část, a vyjadřuje základ řady přirozených logaritmů. Je zvýšena na sílu rovnou zápornému kvocientu aktivační energie (Ea) mezi produktem vzniklým z plynové konstanty (R) a absolutní teplota (T) systému, který je třeba zvážit.
Je třeba poznamenat, že frekvenční faktor lze v určitých reakčních systémech v širokém teplotním rozsahu považovat za konstantní..
Tento matematický výraz původně předpokládal nizozemský chemik Jacobus Henricus van't Hoff v roce 1884, ale ten, kdo mu dal vědeckou platnost a interpretoval jeho premisu, byl švédský chemik Svante Arrhenius, v roce 1889.
Arrheniova rovnice specifikuje přímou proporcionalitu, která existuje mezi rychlostní konstantou reakce a frekvencí kolizí mezi molekulami.
Podobně může být tato rovnice reprezentována pohodlnějším způsobem použitím vlastnosti přirozených logaritmů na každou stranu rovnice a získání:
ln k = ln A - Ea / RT
Přeskupením podmínek z hlediska získání rovnice přímky (y = mx + b) se dosáhne následujícího výrazu:
ln k = (- Ea / R) (1 / T) + ln A
Takže při konstrukci grafu ln k proti 1 / T se získá přímka, kde ln k představuje souřadnici a, (-Ea / R) představuje sklon přímky (m), (1 / T) představuje souřadnice x a ln A představuje průsečík s osou souřadnice (b).
Jak je vidět, sklon vyplývající z tohoto výpočtu se rovná hodnotě -Ea / R. To znamená, že pokud chcete pomocí tohoto výrazu získat hodnotu aktivační energie, musíte provést toto jednoduché objasnění, jehož výsledkem je:
Ea = -mR
Zde je známa hodnota m a R je konstanta rovná 8,314 J / K mol.
Při pokusu o získání obrazu aktivační energie jej lze považovat za bariéru, která neumožňuje reakci mezi molekulami s nižší energií..
Stejně jako v běžné reakci se stává, že počet molekul, které mohou reagovat, je poměrně velký, rychlost - a stejně tak kinetická energie těchto molekul - může být velmi proměnlivá.
Obecně se stává, že pouze malé množství z celku molekul, které prošly srážkou - ty, které mají větší rychlost pohybu - mají dostatek kinetické energie, aby mohly překročit velikost aktivační energie. Takže tyto molekuly jsou vhodné a schopné být součástí reakce.
Podle Arrheniovy rovnice znamená záporné znaménko - které předchází kvocientu mezi aktivační energií a produktem plynové konstanty a absolutní teplotou -, že rychlostní konstanta klesá, protože dochází ke zvýšení aktivační energie, stejně jako růst teploty při zvýšení teploty.
Pro výpočet aktivační energie vytvořením grafu byly podle Arrheniovy rovnice měřeny rychlostní konstanty pro rozkladnou reakci acetaldehydu při pěti různých teplotách a je žádoucí určit aktivační energii pro reakci, která je vyjádřena jako:
CH3CHO (g) → CH4(g) + CO (g)
Data pro pět měření jsou následující:
k (1 / M1/2S): 0,011 - 0,035 - 0,105 - 0,343 - 0,789
T (K): 700 - 730 - 760 - 790 - 810
Za prvé, aby bylo možné vyřešit tuto neznámou a určit aktivační energii, musí být sestaven graf ln k vs 1 / T (y vs x), aby se získala přímka a odtud vezměte sklon a najděte hodnotu Ea , jak bylo vysvětleno.
Při transformaci naměřených dat podle Arrheniovy rovnice [ln k = (- Ea / R) (1 / T) + ln A] jsou pro y a x nalezeny následující hodnoty:
ln k: (-4,51) - (-3,35) - (-2,254) - (-1,070) - (-0,237)
1 / T (K.-1): 1,43 * 10-3 - 1,37 * 10-3 - 1,32 * 10-3 - 1,27 * 10-3 - 1,23 * 10-3
Z těchto hodnot a pomocí matematického výpočtu strmosti - buď v počítači nebo v kalkulačce, pomocí výrazu m = (Ydva-Y1) / (Xdva-X1) nebo pomocí metody lineární regrese - se získá, že m = -Ea / R = -2,09 * 104 K. Tedy:
Ea = (8,314 J / K mol) (2,09 * 104 K)
= 1,74 * 105 = 1,74 * 10dva kJ / mol
K určení dalších aktivačních energií grafickým způsobem se provádí podobný postup.
Zatím žádné komentáře