
Určení translační rovnováhy, aplikace, příklady
The translační rovnováha Je to stav, ve kterém je nalezen objekt jako celek, když jsou kompenzovány všechny síly na něj působící, což má za následek nulovou čistou sílu. Matematicky ekvivalentní tvrzení, že F1+ Fdva + F3 +…. = 0, kde F1, Fdva, F3... zúčastněné síly.
Skutečnost, že tělo je v translační rovnováze, neznamená, že je nutně v klidu. Toto je konkrétní případ výše uvedené definice. Objekt může být v pohybu, ale při absenci zrychlení to bude jednotný přímočarý pohyb.

Pokud je tedy tělo v klidu, pokračuje takto. A pokud již má pohyb, bude mít konstantní rychlost. Pohyb libovolného objektu je obecně složením překladů a rotací. Překlady mohou být, jak je znázorněno na obrázku 2: lineární nebo křivočaré.
Pokud je však jeden z bodů objektu pevný, pak jedinou možností, jak se musí pohybovat, je otáčení. Příkladem toho je CD, jehož střed je pevný. CD má schopnost otáčet se kolem osy, která prochází tímto bodem, ale ne překládat.
Když mají objekty pevné body nebo jsou podporovány na plochách, mluvíme o Odkazy. Spojení interagují a omezují pohyby, které je objekt schopen provádět.
Rejstřík článků
- 1 Stanovení translační rovnováhy
- 1.1 Otočení objektu
- 1.2 Definice točivého momentu
- 1.3 Rovnovážné podmínky
- 2 Aplikace
- 3 Příklady translační rovnováhy
- 3.1 Řešení
- 4 Odkazy
Stanovení translační rovnováhy
U částice v rovnováze je platné zajistit, aby:
FR = 0
Nebo v součtové notaci:
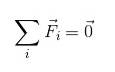
Je zřejmé, že aby tělo bylo v translační rovnováze, musí být síly působící na něj nějakým způsobem kompenzovány, takže jejich výslednice je nulová..
Tímto způsobem objekt nezažije zrychlení a všechny jeho částice jsou v klidu nebo procházejí přímočarými překlady konstantní rychlostí..
Pokud se nyní objekty mohou otáčet, obvykle se budou otáčet. Proto se většina pohybů skládá z kombinací překladu a rotace..
Otáčení objektu
Je-li důležitá rotační rovnováha, může být nutné zajistit, aby se předmět neotáčel. Pak je nutné studovat, zda na to působí momenty nebo momenty.
Točivý moment je vektorová velikost, na které závisí rotace. Vyžaduje použití síly, ale je také důležitý bod použití síly. Chcete-li objasnit myšlenku, zvažte rozšířený objekt, na který působí síla F a podívejme se, jestli je schopen produkovat rotaci kolem nějaké osy O.
Je již intuitivní, že když tlačíte předmět v bodě P silou F, je možné jej otočit kolem bodu O a otáčet se proti směru hodinových ručiček. Důležitý je ale také směr, ve kterém je síla aplikována. Například síla aplikovaná na figuru uprostřed nedovolí objektu otáčet se, i když jím jistě může pohybovat..
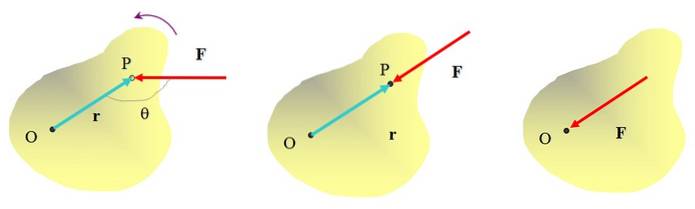
Přímým působením síly na bod O se také předmět nezmění. Je tedy jasné, že k dosažení rotačního účinku musí být síla aplikována v určité vzdálenosti od osy otáčení a její linie působení nesmí projít uvedenou osou..
Definice točivého momentu
Krouticí moment nebo moment síly, označený jako τ, velikost vektoru odpovědná za sestavení všech těchto skutečností, je definován jako:
τ = r x F
Vektor r je směrován od osy otáčení k bodu působení síly a je důležitá účast úhlu mezi r a F. Proto je velikost točivého momentu vyjádřena jako:
τ = r.F.sen co
Nejúčinnější točivý moment nastane, když r Y F jsou kolmé.
Nyní, pokud je žádoucí, aby nedocházelo k žádným rotacím nebo k nim dochází při konstantním úhlovém zrychlení, je nutné, aby součet momentů působících na objekt byl nulový, analogicky k tomu, co bylo uvažováno pro síly:
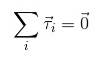
Rovnovážné podmínky
Rovnováha znamená stabilitu, harmonii a rovnováhu. Aby pohyb objektu měl tyto vlastnosti, musí být použity podmínky popsané v předchozích částech:
1) F1+ Fdva + F3 +…. = 0
2) τ1+ τdva + τ3 +…. = 0
První podmínka zaručuje translační rovnováhu a druhá rotační rovnováhu. Obojí musí být splněno, pokud má objekt zůstat uvnitř statická rovnováha (absence pohybu jakéhokoli druhu).
Aplikace
Rovnovážné podmínky jsou použitelné pro mnoho struktur, protože když se staví budovy nebo různé objekty, provádí se to s úmyslem, aby jejich části zůstaly ve stejných vzájemných polohách. Jinými slovy, objekt se nerozebírá.
To je důležité například při stavbě mostů, které zůstávají pevné pod nohama, nebo při navrhování obytných struktur, které nemění polohu nebo nemají sklon k převrácení..
I když se věří, že rovnoměrný přímočarý pohyb je extrémním zjednodušením pohybu, které se v přírodě vyskytuje jen zřídka, je třeba si uvědomit, že rychlost světla ve vakuu je konstantní a také rychlost zvuku ve vzduchu, pokud považujeme médium za homogenní.
V mnoha umělých mobilních strukturách je důležité udržovat konstantní rychlost: například na eskalátorech a montážních linkách.
Příklady translační rovnováhy
Toto je klasické cvičení napětí, které udržuje lampu v rovnováze. Je známo, že lampa váží 15 kg. Najděte velikosti napětí nezbytných k jeho udržení v této poloze.
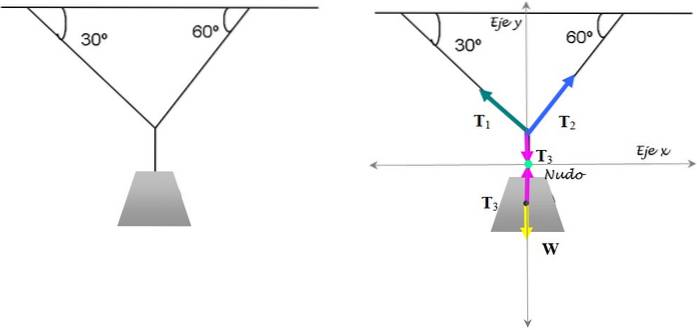
Řešení
Abychom to vyřešili, zaměříme se na uzel, kde se setkávají tři řetězce. Příslušné diagramy volného těla pro uzel a pro lampu jsou zobrazeny na obrázku výše..
Hmotnost lampy je Š = 5 kg. 9,8 m / sdva = 49 N. Aby byla lampa v rovnováze, stačí, aby byla splněna první podmínka rovnováhy:
T3 - W = 0
T3 = W = 49 N.
Napětí T1 Y Tdva musí se rozložit:
T1 rok + T2 a - T3 = 0 (Součet sil podél osy y)
-T1x +T2x = 0 (Součet sil podél osy x)
Použití trigonometrie:
T1.cos 60º + Tdva .cos 30º = 49
- T1.sen60º + Tdva.sin30º = 0
Je to systém dvou rovnic se dvěma neznámými, jejichž odpověď je: T1 = 24,5 N. Y Tdva = 42,4 N.
Reference
- Rex, A. 2011. Základy fyziky. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7ma. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Základy fyziky. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fyzika. Addison Wesley. 332-346.

Zatím žádné komentáře