Vzorec a rovnice náhodných chyb, výpočet, příklady, cvičení

The náhodná chyba fyzikální veličiny se skládá z nepředvídatelných variací míry této veličiny. Tyto variace mohou být způsobeny měřeným jevem, měřicím přístrojem nebo samotným pozorovatelem..

Taková chyba není proto, že se během experimentu něco stalo špatně, ale je to chyba vlastní procesu měření nebo studovanému jevu. To způsobí, že měřená veličina je někdy o něco vyšší a někdy o něco menší, ale obvykle osciluje kolem centrální hodnoty..

Na rozdíl od náhodné chyby může být systematická chyba způsobena špatnou kalibrací nebo nedostatečným faktorem měřítka v měřicím přístroji, dokonce i poruchou experimentálního zařízení nebo nedostatečným pozorováním, které způsobí odchylku ve stejném směru..

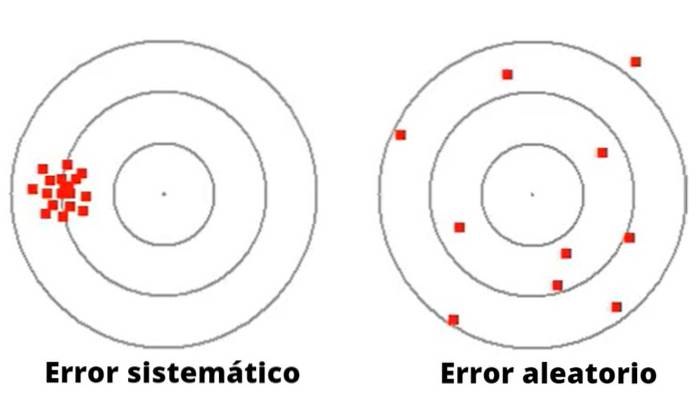
Obrázek 1 ilustruje rozdíl mezi systematickou a náhodnou chybou ve hře hodu šipkami na cíl s kruhy..

V případě levice jsou šipky soustředěny kolem bodu daleko od středu. Spouštěč těchto šipek, i když má dobrý cíl, má systematické selhání, snad vizuálního původu, nebo ve způsobu házení.

Na druhé straně má odpalovací zařízení na pravé straně (na obrázku 1) velkou disperzi kolem středového cíle, proto se jedná o velmi nepřesný spouštěč se špatným zaměřením, který se nedobrovolně dopustí náhodné chyby..

Rejstřík článků

• 1 Vzorce a rovnice v náhodném omylu
  • 1.1 Průměrná hodnota a směrodatná odchylka
• 2 Jak vypočítat náhodnou chybu?
• 3 Příklady náhodných chyb
  • 3.1 Měření délky pomocí svinovacího metru nebo pravítka
  • 3.2 Rychlost větru
  • 3.3 Při odečtu objemu na odměrném válci
  • 3.4 Při měření výšky dítěte
  • 3.5 Při používání koupelnové váhy
• 4 Cvičení vyřešeno
  • 4.1 Řešení
• 5 Reference

Vzorce a rovnice v náhodném omylu

Pokud je v procesu měření pozorována náhodná chyba, je nutné měření opakovat několikrát, protože ze statistického hlediska platí, že čím větší je počet měření, tím menší je chyba v konečném odhadu měření..

Při každém měření je samozřejmě nutné dbát na to, aby podmínky, v nichž jsou prováděny, byly vždy stejné.

Předpokládejme, že se měření opakuje n krát. Protože v každém měření je náhodná chyba, bude mít mírně odlišnou hodnotu. Předpokládejme, že soubor n měření je:

X₁, X_dva, X₃,..., X_n

Jakou hodnotu tedy pro opatření vykázat? 

Průměrná hodnota a směrodatná odchylka

The střední hodnota nebo průměrný souboru opatření, která označujeme a počítá se takto:

= (x₁ + X_dva + X₃ +… + X_n) / n

Standardní odchylka

Tento výsledek však má míru chyby danou směrodatnou odchylkou. Chcete-li to definovat, musíte nejprve znát odchylku a poté rozptyl:

-Odchylka d_i  co má každá naměřená hodnota xi vzhledem k průměrné hodnotě to je:

d_i = x_i -

Pokud by byl vypočítán průměr odchylek, byl by systematicky získáván = 0, tak jako: 

= (d₁ + d_dva + d₃ +… + D._n) / n =

= [(x₁ - ) + (x_dva - ) + ... + (X_n - )] / n

= (x₁+ X_dva +… + X_n) / n - n / n = - = 0

-Průměr odchylek není užitečné znát rozptyl opatření. Na druhou stranu průměrná hodnota druhé mocniny odchylek nebo rozptylu, označená σ^dva, Pokud to je.

Vypočítává se podle následujícího vzorce:

σ^dva = (d₁^dva + d_dva^dva +…. + D._n^dva ) / (n -1)

Ve statistikách se toto množství nazývá rozptyl.  

A druhá odmocnina rozptylu je známá jako směrodatná odchylka σ:

σ = √ [(d₁^dva + d_dva^dva +…. + D._n^dva ) / (n -1)] 

Směrodatná odchylka σ nám říká, že:

1. - 68% provedených měření spadá do daného intervalu [ - σ , + σ]. 

2. - 95% měření je v intervalu [ - 2σ , + 2σ].

3. - 99,7% provedených měření je v rozsahu [ - 3σ , + 3σ].

Jak vypočítat náhodnou chybu?

Výsledkem měření je střední hodnota z n měření označená a počítá se podle následujícího vzorce:

= (∑x_i) / n

nicméně Nejedná se o „přesnou“ hodnotu měření, protože je ovlivněn náhodná chyba ε, který se počítá takto:

ε = σ / √n

Kde:

σ = √ [(∑ (xi - )^dva ) / (n -1)]

Konečný výsledek měření musí být uveden jedním z následujících způsobů:

1. ± σ / √n = ± ε s úrovní spolehlivosti 68%.
2. ± 2σ / √n = ± 2ε s úrovní spolehlivosti 95%.
3. ± 3σ / √n = ± 3ε s úrovní spolehlivosti 99,7%.

Náhodná chyba ovlivňuje poslední významnou postavu měření, která se obecně shoduje s oceněním měřicího přístroje. Pokud je však náhodná chyba velmi velká, mohou být variace ovlivněny poslední dvě významné číslice..

Příklady náhodných chyb

Náhodné chyby se mohou objevit v různých případech, kdy se provádí měření:

Měření délky pomocí svinovacího metru nebo pravítka

Když se délka měří pravítkem nebo svinovacím metrem a naměřené hodnoty spadají mezi značky na stupnici, pak se tato střední hodnota odhadne.

Někdy má odhad přebytek a jindy defekt, takže se do procesu měření zavádí náhodná chyba.

Rychlost větru

Při měření rychlosti větru mohou nastat změny ve čtení z jednoho okamžiku do druhého v důsledku měnící se povahy jevu..

Při čtení objemu na odměrném válci

Když je objem odečítán odměrným válcem, i když se pokoušíme minimalizovat chybu paralaxy, pokaždé, když se měří, úhel pozorování menisku se trochu změní, a proto jsou měření ovlivněna náhodnou chybou.

Při měření výšky dítěte

Při měření výšky dítěte, zejména pokud je trochu neklidné, se malé změny v držení mírně změní v čtení.

Při použití koupelnové váhy

Když chceme měřit naši váhu pomocí stupnice v koupelně, může malá změna osy otáčení, dokonce i změna polohy, náhodně ovlivnit měření..

Cvičení vyřešeno

Dětský kočárek se může sjíždět rovnou a nakloněnou stopou a čas potřebný k cestování po celé stopě se měří stopkami. 

Měření se provádí 11krát, přičemž je třeba dbát na to, aby byl vozík vždy uvolněn ze stejného místa, aniž by na něj byl vydáván jakýkoli impuls a udržován sklon..

Soubor získaných výsledků je:

3.12s 3.09s 3.04s 3.04s 3.10s 3.08s 3.05s 3.10s 3.11s 3.06s, 3.03s

Jaká je náhodná chyba měření?

Řešení

Jak vidíte, získané výsledky nejsou jedinečné a mírně se liší..

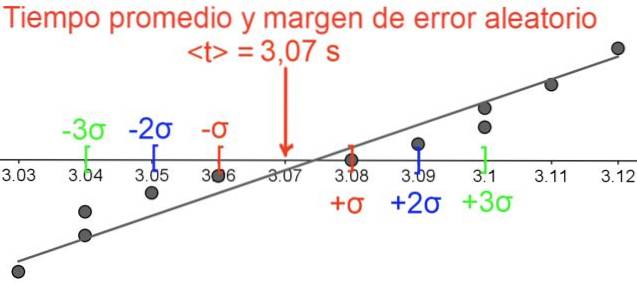
První věcí je vypočítat průměrnou hodnotu doby sestupu, získat 3,074545455 sekund.

Nemá smysl uchovávat tolik desetinných míst, protože každé měření má tři platné číslice a druhé desetinné místo každého měření je nejisté, protože je na hranici zhodnocení stopek, proto se výsledek zaokrouhlí na dvě desetinná místa:

= 3,08 s.

U kalkulačky ve statistickém režimu je směrodatná odchylka σ = 0,03 s a standardní chyba je σ / √11 = 0,01 s. Konečný výsledek je vyjádřen takto:

Čas sestupu 

3,08 s ± 0,01 s (s úrovní spolehlivosti 68%)

3,08 s ± 0,02 s (s 95% úrovní spolehlivosti)

3,08 s ± 0,03 s (s úrovní spolehlivosti 99,7%)

Reference

1. Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
2. Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
3. Helmenstine A. Náhodná chyba vs. systematická chyba. Obnoveno z: thoughtco.com
4. Laredo, E. Chyby v médiích. Obnoveno z: usb.ve.
5. Levin, R. 1988. Statistiky pro správce. 2. místo Edice. Hala Prentice.