Tok elektrického pole

Co je tok elektrického pole?

The tok elektrického pole nebo jednoduše elektrický tok je skalární veličina úměrná počtu čar elektrického pole, které procházejí povrchem. Označuje se velkým řeckým písmenem Φ (phi).

Elektrické pole ve skutečnosti „neproudí“ tak, jak to dělá proud vody, ačkoli proudnice tekutiny se podobají proudům elektrického pole..

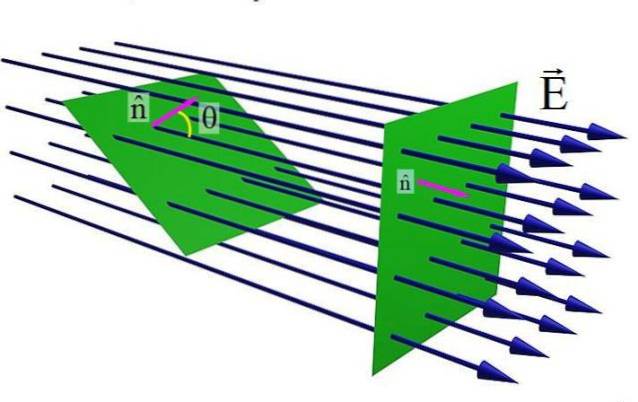
Obrázek výše ukazuje rovný povrch procházející elektrickým polem A. Když je jednotkový vektor kolmý k povrchu n a pole A jsou paralelní, počet siločar, které procházejí povrchem, je maximální. Ale jako úhel θ mezi n Y A, počet linek procházejících zeleným povrchem je menší.

Na druhé straně tok elektrického pole také závisí na velikosti A, protože čím větší je, tím více siločárů protíná povrch. A samozřejmě, čím větší je plocha S uvedeného povrchu, tím větší je tok, takže je stanovena následující rovnice:

Φ = E ∙ Scosθ

Tento výraz je v souladu s bodovým produktem mezi vektory A Y n:

Φ = (A • n) S

Jednotka pro tok elektrického pole v SI mezinárodním systému jednotek je N.m^dva/ C (newton x metr čtvereční / coulomb). Alternativně, protože pole se také měří ve V / m (volt na metr), elektrický tok zůstává v (V ∙ m).

Příklady

Podle definice může být elektrický tok kladný, záporný nebo rovný 0. Tok elektrického pole je:

-Pozitivní, když úhel θ mezi A Y n je menší než 90 °, protože cos θ je větší než nula.

-Záporné, je-li uvedený úhel větší než 90 °, protože cos θ je menší než nula.

-Null, když θ je přesně 90 °, protože cos 90 ° = 0 a siločáry jsou v tomto případě tangenciální k povrchu.

-Na druhou stranu, pokud je úhel mezi A Y n je rovno 0, tok získává svou maximální hodnotu.

Tyto možnosti jsou zobrazeny na následujícím obrázku:

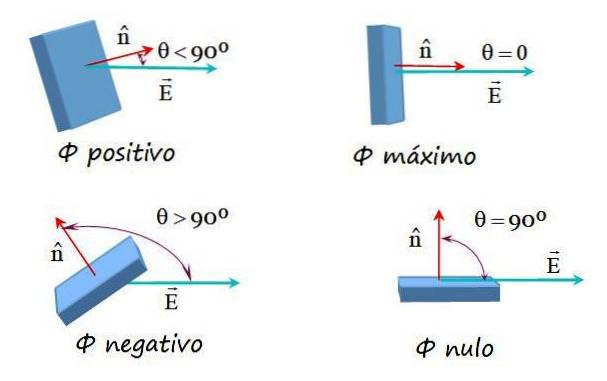
Tok elektrického pole na libovolném povrchu

Dříve byl tok elektrického pole určen v konkrétním případě rovnoměrného pole dopadajícího na rovný povrch. Pro povrch libovolného tvaru S a / nebo nerovnoměrné elektrické pole úhel mezi A Y n se může lišit bod od bodu.

Na následujícím obrázku jsou dva příklady, vlevo zakřivený povrch a vpravo uzavřený povrch.

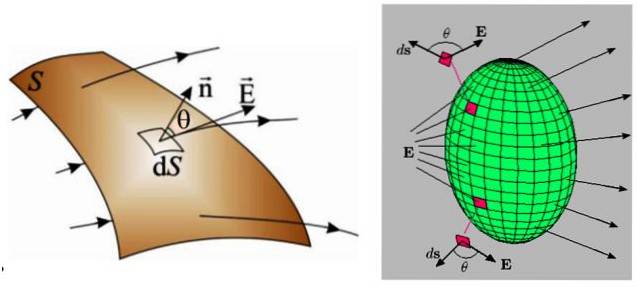
V obou případech je povrch rozdělen do mnohem menších oblastí nekonečně malé velikosti, zvaných dS, kterými prochází tok také nekonečně malá dΦ:

dΦ = (A•n) dS = (Ecosθ) dS

Celkové pole se získá sečtením všech těchto nekonečně malých příspěvků:

V případě uzavřených povrchů, n vždy směřuje ven, proto má tok znaménko +, když je výběžek k S, protože úhel mezi A Y n je menší než 90 °, a znaménko - když pole přichází, protože pak úhel mezi A Y n je větší než 90 ° (viz obrázek 2).

Všimněte si, že v uzavřené ploše vpravo je počet siločar vstupujících na povrch roven počtu opouštějících čar. Čistý tok, definovaný jako algebraický součet příchozího a odchozího toku, je tedy nula.

Zdroj elektrického pole je v tomto případě mimo povrch, avšak čistý tok by se lišil od 0, pokud by zdroj elektrického pole (distribuce nábojů) byl uvnitř povrchu..

Výcvik

Cvičení 1

Má elektrické pole A = 3,5 kN / C X a plochý obdélníkový povrch široký 0,35 ma dlouhý 0,7 m. Tok elektrického pole přes obdélník najdete v následujících případech:

a) Povrch je rovnoběžný s rovinou yz.

b) Obdélník je rovnoběžný s rovinou xy.

c) Normála roviny svírá s osou x úhel 40 ° a obsahuje osu y.

Řešení

Normální vektor a vektor elektrického pole jsou rovnoběžné, proto je úhel θ mezi nimi 0 ° a elektrický tok je:

Φ = (E ∙ S) cos 0 = E ∙ S

Oblast S obdélníku je:

S = 0,35 m x 0,7 m = 0,245 m^dva

Nahrazení v Φ:

Φ = E ∙ S = 3,5 x 10³ N / C × 0,245 m^dva = 857,5 Nm^dva / C..

Řešení b

Tok elektrického pole je 0, protože vektory A Y n jsou na sebe kolmé.

Řešení c

Úhel θ mezi polem A a normální vektor n je 40 ° (viz obrázek), proto:

Φ = E ∙ S ∙ cos θ = 3,5 x 10³ N / C × 0,245 m^dva × cos 40º = 656,9 N ∙ m^dva / C..

Cvičení 2

Vypočítejte tok elektrického pole, který vytváří kladný bodový náboj q_nebo = 2μC umístěné ve středu koule o poloměru R = 5 cm.

Řešení

Pole produkované nábojem q_nebo Není to jednotné, ale z Coulombova zákona je známo, že na povrchu koule má velikost:

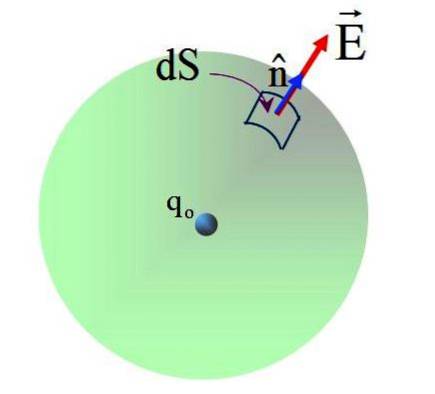
Pole má radiální směr a normální vektor n, proto je úhel mezi oběma vektory 0 v každém bodě sférické plochy. Nahrazení v:

Musí:

Integrál dS na celé sférické ploše S je jeho plocha, která je 4πR^dva, Tím pádem:

Jeho hodnota je:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m^dva/ C = 2,3 x 10⁵ N⋅m^dva/ C.

Reference

1. Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
2. Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 5. Elektrostatika. Upravil Douglas Figueroa (USB).
3. Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
4. Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
5. Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vyd. 1. díl Pearson.