
Vzorec absolutní frekvence, výpočet, rozdělení, příklad
The Absolutní frekvence Je definována jako počet opakování stejných dat v rámci sady pozorování numerické proměnné. Součet všech absolutních frekvencí odpovídá součtu dat.
Pokud máte mnoho hodnot statistické proměnné, je vhodné je vhodně uspořádat, abyste získali informace o jejím chování. Tyto informace jsou dány měřítky centrální tendence a mírou rozptylu..
Ve výpočtech těchto opatření jsou data reprezentována frekvencí, s jakou se objevují ve všech pozorováních..
Následující příklad ukazuje, jak odhalující je absolutní frekvence každé části dat. Během první poloviny května to byly nejprodávanější velikosti koktejlových šatů ze známého obchodu s dámským oblečením:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
Kolik šatů se prodává v konkrétní velikosti, například velikosti 10? Majitelé mají zájem vědět o objednávce.
Pořadí dat usnadňuje počítání, celkem je přesně 30 pozorování, která jsou seřazená od nejmenší po největší:
4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18
A nyní je zřejmé, že velikost 10 se opakuje 6krát, proto je její absolutní frekvence rovna 6. Stejný postup se provádí ke zjištění absolutní frekvence zbývajících velikostí..
Rejstřík článků
- 1 vzorce
- 1.1 Jiné frekvence
- 2 Jak získat absolutní frekvenci?
- 2.1 Tabulka
- 2.2 Rozšířená tabulka kmitočtů
- 3 Distribuce frekvence
- 3.1 Distribuce frekvence pro seskupená data
- 4 Příklad
- 5 Cvičení vyřešeno
- 5.1 Řešení
- 6 Reference
Vzorce
Absolutní frekvence, označená jako fi, se rovná počtu opakování určité hodnoty Xi je ve skupině pozorování.
Za předpokladu, že součet pozorování je N hodnot, musí být součet všech absolutních frekvencí roven tomuto počtu:
∑fi = f1 + Fdva + F3 +... fn = N
Jiné frekvence
Pokud každá hodnota fi děleno celkovým počtem dat N, máme relativní frekvence Fr hodnoty X.i:
Fr = fi / N
Relativní frekvence jsou hodnoty mezi 0 a 1, protože N je vždy větší než jakékoli fi, ale součet se musí rovnat 1.
Vynásobením každé hodnoty f 100r máš procentní relativní frekvence, jehož součet je 100%:
Procentní relativní frekvence = (fi / N) x 100%
Důležité je také kumulativní frekvence Fi do určitého pozorování je to součet všech absolutních frekvencí až do uvedeného pozorování včetně:
Fi = f1 + Fdva + F3 +... fi
Pokud je akumulovaná frekvence vydělena celkovým počtem dat N, máme kumulativní relativní frekvence, který vynásobený 100 dává procento kumulativní relativní frekvence.
Jak získat absolutní frekvenci?
Chcete-li zjistit absolutní frekvenci určité hodnoty, která patří do souboru dat, jsou všechny uspořádány od nejnižší po nejvyšší a je spočítán počet zobrazení hodnoty.
V příkladu velikostí šatů je absolutní frekvence velikosti 4 3 šaty, tj. F1 = 3. U velikosti 6 byly prodány 4 šaty: fdva = 4. Ve velikosti 8 byly také prodány 4 šaty, např3 = 4 a tak dále.
Tabulka
Celkové výsledky lze vyjádřit v tabulce, která zobrazuje absolutní frekvence každého z nich:
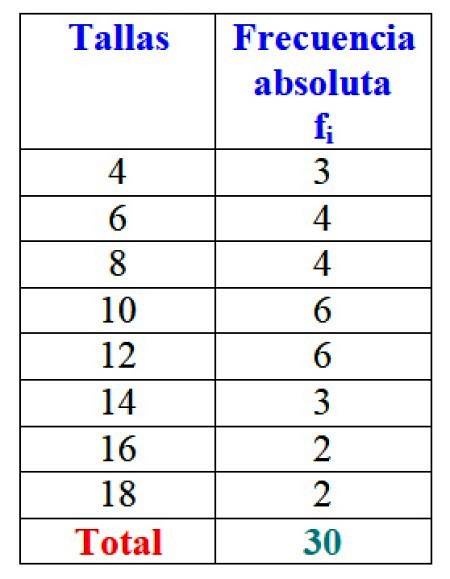
Je zřejmé, že je výhodné uspořádat si informace a mít k nim přístup na první pohled místo práce s jednotlivými daty.
Důležité: Všimněte si, že při přidání všech hodnot sloupce fi vždy získáte celkový počet dat. Pokud ne, musíte zkontrolovat účetnictví, protože došlo k chybě.
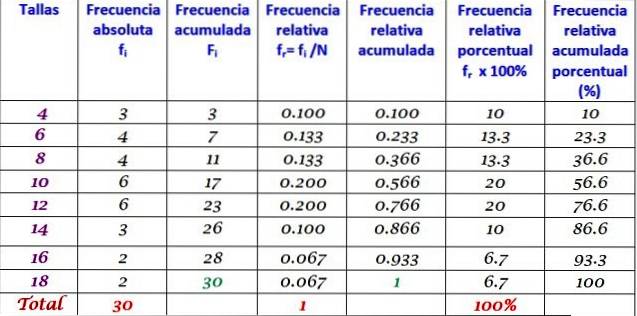
Rozšířená tabulka kmitočtů
Výše uvedenou tabulku lze rozšířit přidáním dalších typů frekvencí do po sobě jdoucích sloupců vpravo:
Distribuce frekvence
Distribuce kmitočtů je výsledkem uspořádání dat z hlediska jejich frekvencí. Když pracujete s mnoha daty, je vhodné je seskupit do kategorií, intervalů nebo tříd, přičemž každá má příslušnou frekvenci: absolutní, relativní, akumulovanou a procentuální..
Jejich cílem je snazší přístup k informacím obsaženým v datech a jejich správná interpretace, což není možné, pokud jsou uvedeny v žádném pořadí..
V příkladu velikostí nejsou data seskupena, protože to není příliš mnoho velikostí a lze s nimi snadno manipulovat a účtovat. Kvalitativní proměnné lze také zpracovat tímto způsobem, ale když jsou data velmi početná, je lepší pracovat jejich seskupením do tříd.
Distribuce frekvence pro seskupená data
Chcete-li seskupit svá data do tříd stejné velikosti, zvažte následující:
-Velikost, šířka nebo šířka třídy: je rozdíl mezi nejvyšší hodnotou ve třídě a nejnižší.
O velikosti třídy se rozhoduje vydělením hodnosti R počtem uvažovaných tříd. Rozsah je rozdíl mezi maximální hodnotou dat a nejmenší, například takto:
Velikost třídy = Hodnocení / Počet tříd.
-Limit třídy: interval od spodní hranice k horní hranici třídy.
-Známka třídy: je střed intervalu, který je považován za reprezentativní pro třídu. Vypočítává se s polovičním součtem horní hranice a dolní hranice třídy.
-Počet tříd: Sturgesův vzorec lze použít:
Počet tříd = 1 + 3 322 log N
Kde N je počet tříd. Protože se obvykle jedná o desítkové číslo, zaokrouhlí se na další celé číslo.
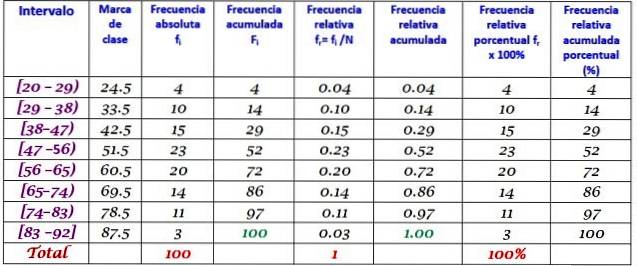
Příklad
Stroj ve velké továrně je mimo provoz kvůli opakujícím se poruchám. Následné periody nečinnosti uvedeného stroje v minutách jsou zaznamenány níže s celkovým počtem 100 dat:
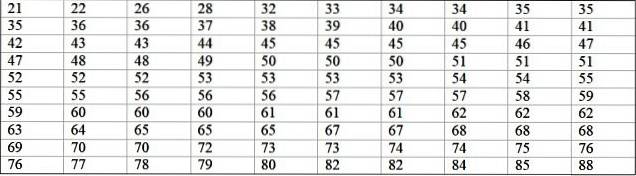
Nejprve se určí počet tříd:
Počet tříd = 1 + 3 322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8
Velikost třídy = Rozsah / Počet tříd = (88-21) / 8 = 8,375
Je to také desetinné číslo, takže 9 je bráno jako velikost třídy.
Značka třídy je průměr mezi horní a dolní hranicí třídy, například pro třídu [20–29) je známka:
Značka třídy = (29 + 20) / 2 = 24,5
Stejným způsobem postupujeme při hledání třídních značek zbývajících intervalů.
Cvičení vyřešeno
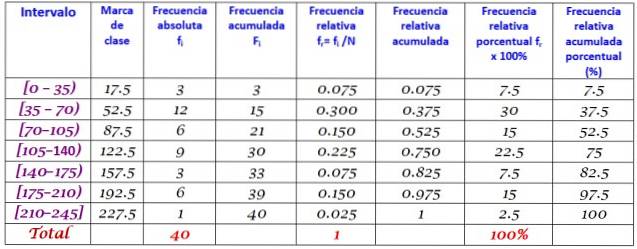
40 mladých lidí uvedlo, že čas v minutách, který minulou neděli strávili na internetu, je následující, seřazený podle vzestupu:
0; 12; dvacet; 35; 35; 38; 40; Čtyři pět; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Je žádáno, aby vytvořili frekvenční rozdělení těchto dat.
Řešení
Rozsah R sady dat N = 40 je:
R = 220 - 0 = 220
Použití vzorce Sturges k určení počtu tříd přináší následující výsledek:
Počet tříd = 1 + 3 322 log N = 1 + 3,32 log 40 = 6,3
Jelikož se jedná o desetinnou čárku, okamžité celé číslo je 7, proto jsou data seskupena do 7 tříd. Každá třída má šířku:
Velikost třídy = Hodnocení / Počet tříd = 220/7 = 31.4
Blízká a kulatá hodnota je 35, proto je zvolena šířka třídy 35.
Značky třídy se počítají zprůměrováním horní a dolní meze každého intervalu, například pro interval [0,35):
Značka třídy = (0 + 35) / 2 = 17,5
Stejným způsobem postupujte iu ostatních tříd.
Nakonec jsou frekvence vypočítány podle postupu popsaného výše, což má za následek následující rozdělení:
Reference
- Berenson, M. 1985. Statistiky pro management a ekonomiku. Interamericana S.A.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Levin, R. 1988. Statistiky pro správce. 2. místo Edice. Hala Prentice.
- Spiegel, M. 2009. Statistiky. Série Schaum. 4. místo Edice. Mcgraw kopec.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.



Zatím žádné komentáře