Druhy tření, koeficient, výpočet, cvičení

The tření je odpor vůči posunutí jednoho povrchu, který je v kontaktu s druhým. Jedná se o povrchový jev, který se vyskytuje mezi pevnými, kapalnými a plynnými materiály. Odporová síla tangenciální ke dvěma povrchům v kontaktu, která působí proti směru relativního posunu mezi uvedenými povrchy, se také nazývá třecí síla nebo třecí síla F_r.

Chcete-li pohybovat pevným tělesem na povrchu, musíte použít vnější sílu, která může překonat tření. Když se tělo pohybuje, třecí síla působí na tělo, zpomaluje ji a může ji dokonce zastavit..

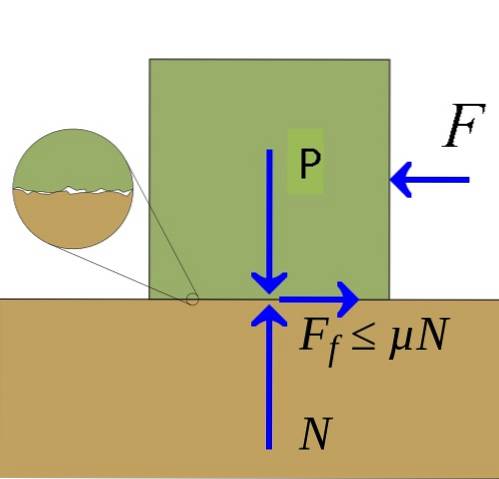
Třecí sílu lze graficky znázornit silovým diagramem tělesa v kontaktu s povrchem. V tomto diagramu třecí síla F_r je nakreslen proti složce síly působící na tělo tangenciálně k povrchu.

Kontaktní plocha vyvíjí na tělo reakční sílu zvanou normální síla N. V některých případech je normální síla způsobena pouze hmotností P těla spočívajícího na povrchu, a v ostatních případech je to způsobeno působením jiných sil než gravitační síly.

Tření nastává, protože mezi dotykovými povrchy jsou mikroskopické drsnosti. Při pokusu o pohyb jednoho povrchu přes druhý dochází ke tření mezi drsnostmi, které brání volnému pohybu na rozhraní. Na druhé straně dochází ke ztrátám energie ve formě tepla, které se nepoužívá k pohybu těla.

Rejstřík článků

• 1 Druhy tření
  • 1,1 -Coulombovo tření
  • 1.2 - Tření kapaliny
  • 1.3 -Třepy stoků
• 2 Koeficienty tření
  • 2.1 Koeficient statického tření
  • 2.2 Koeficient kinetického tření
  • 2.3 Koeficient pružného tření
  • 2.4 Molekulární koeficient tření
• 3 Jak se počítá tření?
  • 3.1 Charakteristika normálu
• 4 Vyřešená cvičení
  • 4.1 - Třecí síla předmětu, který spočívá na vodorovném povrchu
  • 4,2 - Třecí síla objektu působícího silou s úhlem sklonu
  • 4.3 - Tření v jedoucím vozidle
• 5 Reference

Druhy tření

Existují dva hlavní typy tření: tření Coulomb nebo suché tření a kapalinové tření.

-Coulombovo tření

Tření Coulomb vždy se staví proti pohybu těles a dělí se na dva typy tření: statické tření a kinetické (nebo dynamické) tření.

Při statickém tření nedochází k pohybu těla na povrchu. Působící síla je velmi malá a nestačí k překonání třecí síly. Tření má maximální hodnotu, která je úměrná normální síle a nazývá se statická třecí síla F_re.

Síla statického tření je definována jako maximální síla, která odolává začátku pohybu těla. Když použitá síla překročí statickou třecí sílu, zůstane na své maximální hodnotě.

Kinetické tření působí, když je tělo již v pohybu. Síla potřebná k udržení pohybu těla v tření se nazývá kinetická třecí síla. F_rc.

Kinetická třecí síla je menší nebo stejná jako statická třecí síla, protože jakmile se tělo začne hýbat, je snazší se hýbat, než se o to pokoušet v klidu..

Coulombovy zákony tření

1. Třecí síla je přímo úměrná síle kolmé ke kontaktní ploše. Konstanta proporcionality je koeficient tření μ který existuje mezi povrchy v kontaktu.
2. Třecí síla je nezávislá na velikosti zjevné kontaktní plochy mezi povrchy.
3. Kinetická třecí síla je nezávislá na klouzavé rychlosti těla.

-Tření kapaliny

Tření nastává také při pohybu těles v kontaktu s kapalnými nebo plynnými materiály. Tento typ tření se nazývá tření kapaliny a je definován jako odpor vůči pohybu těles v kontaktu s kapalinou.

Tření kapaliny také označuje odpor kapaliny protékat při kontaktu s vrstvami kapaliny ze stejného nebo jiného materiálu a závisí na rychlosti a viskozitě kapaliny. Viskozita je míra odporu kapaliny proti pohybu.

-Stokesovo tření

Stokesovo tření je druh kapalinového tření, při kterém sférické částice ponořené do viskózní kapaliny, v laminárním proudění, zažívají třecí sílu, která zpomaluje jejich pohyb v důsledku kolísání molekul tekutiny..

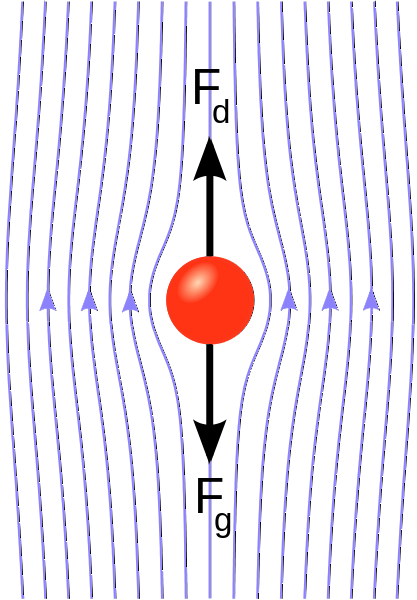
Tok je laminární, když jsou viskózní síly, které působí proti pohybu kapaliny, větší než setrvačné síly a kapalina se pohybuje dostatečně malou rychlostí a přímočarou cestou.

Koeficienty tření

Podle prvního třecího zákona Coulomb koeficient tření μ se získá ze vztahu mezi třecí silou a silou kolmou ke kontaktní ploše.

μ = F_r/N

Koeficient μ je to bezrozměrná veličina, protože jde o vztah mezi dvěma silami, který závisí na povaze a zacházení s materiály v kontaktu. Obecně je hodnota koeficientu tření mezi 0 a 1.

Statický koeficient tření

Koeficient statického tření je konstanta proporcionality, která existuje mezi silou, která brání pohybu těla v klidovém stavu na kontaktní ploše, a silou kolmou k povrchu..

μ_a= F_re/ N

Kinetický koeficient tření

Koeficient kinetického tření je konstanta proporcionality, která existuje mezi silou, která omezuje pohyb tělesa pohybujícího se na povrchu, a silou kolmou k povrchu..

μ_C= F_rc/ N

Koeficient statického tření je větší než koeficient kinetického tření.

μ_s> μ_C

Součinitel pružného tření

Elastický koeficient tření je odvozen od tření mezi kontaktními povrchy elastických, měkkých nebo drsných materiálů, které jsou deformovány působícími silami. Tření je proti relativnímu pohybu mezi dvěma elastickými povrchy a posunutí je doprovázeno elastickou deformací povrchových vrstev materiálu..

Koeficient tření získaný za těchto podmínek závisí na stupni drsnosti povrchu, fyzikálních vlastnostech kontaktovaných materiálů a velikosti tangenciální složky smykové síly na rozhraní materiálů..

Koeficient molekulárního tření

Koeficient molekulárního tření se získává ze síly, která omezuje pohyb částice, která klouže po hladkém povrchu nebo kapalinou.

Jak se počítá tření?

Třecí síla na pevných rozhraních se vypočítá pomocí rovnice F_r = μN

N je normální síla a μ je koeficient tření.

V některých případech se normální síla rovná hmotnosti těla P. Hmotnost se získá vynásobením hmotnosti m gravitačního zrychlení těla G.

P= mg

Dosazením rovnice hmotnosti do rovnice třecí síly dostaneme:

F_r = μmg

Charakteristika normálu

Když je objekt v klidu na rovném povrchu, normální síla je síla vyvíjená povrchem na tělo a staví se proti síle gravitací podle Newtonova zákona akce a reakce..

Normální síla působí vždy kolmo na povrch. Na svažitém povrchu se normála zmenšuje, jak se zvětšuje úhel náklonu, a ukazuje v kolmém směru od povrchu, zatímco váha směřuje svisle dolů. Rovnice normálové síly na šikmém povrchu je:

N = mgcosθ

θ = úhel sklonu kontaktní plochy.

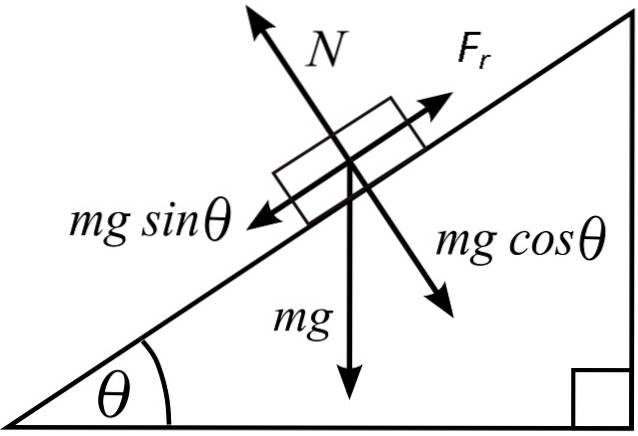
Složka síly působící na tělo k jejímu posunutí je:

F = mgsenθ

Jak se použitá síla zvyšuje, přibližuje se k maximální hodnotě třecí síly, tato hodnota odpovídá hodnotě statické třecí síly. Když  F = F_re, statická třecí síla je:

F_re= mgsenθ

A koeficient statického tření se získá tečnou úhlu sklonu θ.

μ_a = soθ

Vyřešená cvičení

-Třecí síla předmětu ležícího na vodorovné ploše

Krabice o hmotnosti 15 kg umístěná na vodorovném povrchu je tlačena osobou, která aplikuje 50 newtonovou sílu na povrch, aby se pohybovala, a poté aplikuje sílu 25 N, aby se box pohyboval konstantní rychlostí. Určete koeficienty statického a kinetického tření.

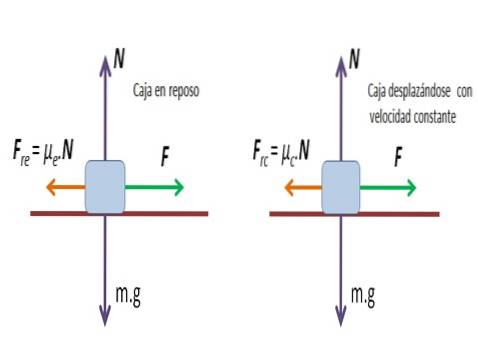
Řešení: S hodnotou síly působící na pohyb pole se získá koeficient statického tření μ_a.

μ_a= F_re/ N

Normální síla N na povrch se rovná hmotnosti krabice, takže N = např

N = 15 kg x 9,8 m / s^dva

N = 147 Nové

V tomto případě, μ_a= 50Novinka / 147Novinka

μ_a= 0,34

Síla použitá k udržení konstantní rychlosti skříně je kinetická třecí síla, která se rovná 25New.

Koeficient kinetického tření se získá z rovnice μ_C= F_rc / N

μ_C= 25Novinka / 147Novinka

μ_C= 0,17

-Třecí síla předmětu působením síly s úhlem sklonu

Muž působí silou na krabici o hmotnosti 20 kg s úhlem působení 30 ° vzhledem k povrchu, na kterém spočívá. Jaká je velikost síly působící na pohyb pole, pokud je koeficient tření mezi schránkou a povrchem 0,5?

Řešení: Aplikovaná síla a její vertikální a horizontální složky jsou znázorněny ve schématu volného těla.

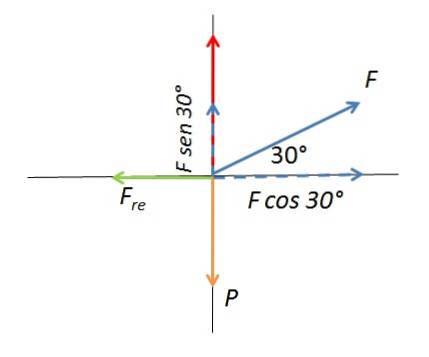
Použitá síla svírá s vodorovným povrchem úhel 30 °. Svislá složka síly se přidává k normální síle ovlivňující sílu statického tření. Krabice se pohybuje, když vodorovná složka aplikované síly překročí maximální hodnotu třecí síly F_re. Rovnice vodorovné složky síly se složkou statického tření dává:

F_re = Fcosθ                       [1]

F_re= μ_a.N                          [dva]

μ_a.N = Fcosθ                      [3]

normální síla

Normální síla již není váhou těla v důsledku svislé složky síly.

Podle druhého Newtonova zákona je součet sil působících na skříň na svislé ose nulový, proto je svislá složka zrychlení na_Y= 0. Normální síla se získá ze součtu

F sin30 ° + N - P = 0                      [4]

P = např                                        [5]

F sin 30 ° + N - m.g = 0                [6]

N = m.g - F sin 30 °                      [7]

Dosazením rovnice [7] do rovnice [3] získáte toto:

μ_a. (m.g - F sin 30 °) = Fcos30 °     [8]

Vymaže se F z rovnice [8] a získáme:

F = μ_a . m.g / (cos 30 ° + μ_a hřích 30 °) = 0,5 x 20 kg x 9,8 m / s^dva / (0,87+ (0,5 x 0,5)) =

F = 87,5 Novinka

-Tření v jedoucím vozidle

1,5tunové vozidlo jede po rovné a vodorovné silnici rychlostí 70 km / h. Řidič vidí na silnici v určité vzdálenosti překážky, které ho nutí prudce brzdit. Po brzdění vozidlo na krátkou dobu dostává smyk, dokud se nezastaví. Pokud je koeficient tření mezi pneumatikami a vozovkou 0,7; určit následující:

1. Jaká je hodnota tření při smyku vozidla?
2. Zpomalení vozidla
3. Vzdálenost ujetá vozidlem od brzdění po zastavení.

Řešení:

Odstavec a

Diagram volného těla ukazuje síly působící na vozidlo při smyku..

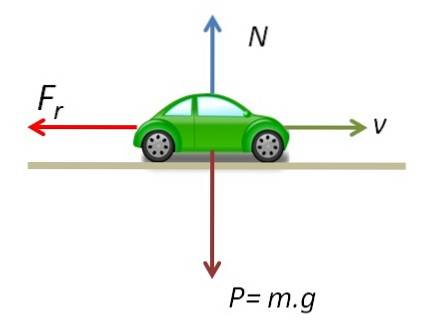
Jelikož součet sil působících na svislou osu je nulový, rovná se normální síla hmotnosti vozidla.

N = např

m = 1,5 t = 1500 kg

N = 1 500 kg x 9,8 m / s^dva= 14700Nový

Třecí síla vozidla při smyku je:

F_r = μN = 0,7x14700Nový

= 10290 Novinka

Část b

Třecí síla ovlivňuje zpomalení vozidla při smyku.

Použitím druhého Newtonova zákona se hodnota zpomalení získá řešením pro rovnici F = m.a.

a = F / m

a = (-10290 nových) / 1 500 kg

= -6,86 m / s^dva

Oddíl c

Počáteční rychlost vozidla je proti₀ = 70 km / h = 19,44 m / s

Když se vozidlo zastaví, jeho konečná rychlost je proti_F = 0 a zpomalení je a = -6,86 m / s^dva

Vzdálenost ujetá vozidlem, od brzdění po zastavení, se získá uvolněním d z následující rovnice:

proti_F^dva = v₀^dva+2ad

d = (v_F^dva - proti₀^dva) / 2

= ((0)^dva-(19,44 m / s)^dva) / (2x (-6,86 m / s^dva))

d = 27,54 m

Vozidlo jede 27,54 m před zastavením pryč.

 Reference

1. Výpočty koeficientu tření za podmínek pružného kontaktu. Mikhin, N M. 2, 1968, Soviet Materials Science, sv. 4, str. 149-152.
2. Blau, P J.. Třecí věda a technologie. Florida, USA: CRC Press, 2009.
3. Vztah mezi adhezními a třecími silami. Israelachvili, J. N., Chen, You-Lung a Yoshizawa, H. 11, 1994, Journal of Adhéze Science and Technology, sv. 8, str. 1231-1249.
4. Zimba, J. Síla a pohyb. Baltimore, Maryland: The Johns Hopkins University Press, 2009.
5. Bhushan, B. Principy a aplikace tribologie. New York: John Wiley and Sons, 1999.
6. Sharma, CS a Purohit, K.. Teorie mechanismů a strojů. Nové Dillí: Prentice Hall of India, 2006.