
Plošné a smykové síly smykové síly
The smyková síla Jedná se o složenou sílu, která je charakterizována tím, že je rovnoběžná s povrchem, na který působí, a má tendenci rozdělit tělo a přemístit úseky vyplývající z řezu..
Je to schematicky znázorněno na obrázku 1, na kterém je znázorněna řezná síla působící na dva různé body dřevěné tužky. Smyková síla zase vyžaduje dvě rovnoběžné a opačné síly, které jsou podle své intenzity schopné tužku deformovat nebo definitivně zlomit..
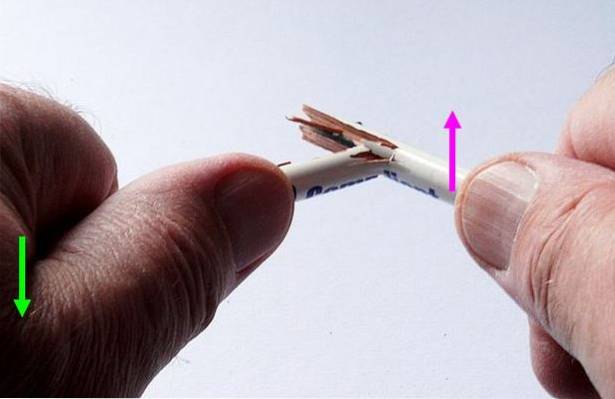
Takže i když mluvíme o smykové síle v jednotném čísle, ve skutečnosti platí dva síly, protože smyková síla je a složená síla. Tyto síly se skládají ze dvou sil (nebo více, ve složitých případech) aplikovaných v různých bodech na objekt.
Dvě síly stejné velikosti a opačného směru, ale s paralelními liniemi působení, tvoří a točivý moment. Točivé momenty neposkytují objektům překlad, protože jejich výslednice je nulová, ale poskytují čistý točivý moment.
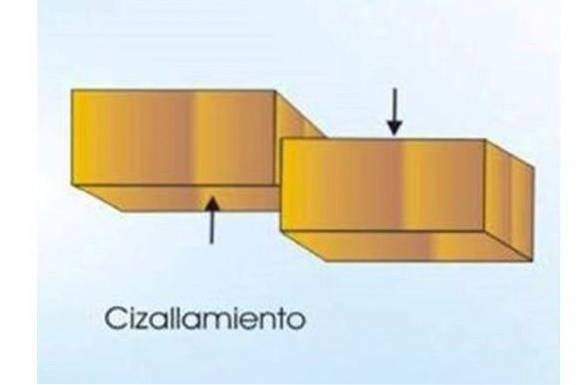
U páru se předměty, jako je volant vozidla, otáčejí nebo se mohou deformovat a rozbít, jako v případě tužky a dřevěné desky zobrazené na obrázku 2.
Rejstřík článků
- 1 Povrchové síly a síly hmoty
- 1.1 Jednoduché síly a složené síly
- 2 Smykové napětí
- 2.1 Stres a napětí
- 2.2 Modul smyku
- 3 Odkazy
Povrchové síly a masové síly
Složené síly jsou součástí tzv povrchové síly, právě proto, že jsou aplikovány na povrch těles a nijak nesouvisí s jejich hmotou. Abychom objasnili bod, porovnejme tyto dvě síly, které často působí na objekty: hmotnost a třecí síla..
Velikost hmotnosti je P = mg a protože to závisí na hmotnosti těla, nejedná se o povrchovou sílu. Je to hromadná síla, a hmotnost je nejcharakterističtějším příkladem.
Tření však závisí na povaze kontaktních ploch a nikoli na hmotnosti těla, na které působí, proto je dobrým příkladem povrchových sil, které se často objevují..
Jednoduché síly a složené síly
Povrchové síly mohou být jednoduchý nebo sloučenina. Už jsme viděli příklad složené síly ve smykové síle a pro svou část je tření reprezentováno jako jednoduchá síla, protože k jeho znázornění v izolovaném tělesném diagramu objektu stačí jediná šipka..
Jednoduché síly jsou odpovědné za tisk změn v pohybu těla, například víme, že kinetická třecí síla mezi pohybujícím se objektem a povrchem, na kterém se pohybuje, má za následek snížení rychlosti.
Naopak, složené síly mají tendenci deformovat tělesa a v případě nůžek nebo nůžek může být konečným výsledkem řez. Další povrchové síly, jako je napětí nebo tlak, prodlužují nebo stlačují tělo, na které působí.
Pokaždé, když je rajče nakrájeno na přípravu omáčky nebo nůžky na řezání listu papíru, platí popsané zásady. Řezné nástroje mají obvykle dva ostré kovové nože, které působí smykovou silou na průřez řezaného předmětu..

Smykové napětí
Účinky smykové síly závisí na velikosti síly a oblasti, na kterou působí, takže při konstrukci koncepce smykové napětí, která bere v úvahu sílu i plochu.
Toto úsilí má další významy, jako je pevnost ve smyku nebo smykové napětí a u stavebních konstrukcí je nesmírně důležité to vzít v úvahu, protože mnoho poruch ve strukturách pochází z působení smykových sil.
Jeho užitečnost je okamžitě pochopena, když vezmeme v úvahu následující situaci: Předpokládejme, že máte dvě tyče ze stejného materiálu, ale různé tloušťky, které jsou vystaveny rostoucím silám, dokud se nerozlomí..
Je zřejmé, že k rozbití tlustší tyčinky musí být použita větší síla, avšak úsilí je stejné pro jakoukoli tyčinku, která má stejné složení. Takové testy jsou ve strojírenství časté, vzhledem k důležitosti výběru správného materiálu pro optimální fungování promítané konstrukce..
Stres a napětí
Matematicky, pokud je smykové napětí označeno jako τ, K velikosti aplikované síly jako F a do oblasti, nad kterou působí jako A, máme průměrné smykové napětí:
τprůměrný= F / A
Jde o poměr mezi silou a plochou, jednotkou úsilí v mezinárodním systému je newton / mdva, s názvem Pascal a zkráceně Pa. V anglickém systému se používá síla / stopa libry dva a libra síla / palecdva.
V mnoha případech se však předmět vystavený smykovému napětí deformuje a poté, co napětí přestane působit, obnoví svůj původní tvar, aniž by se skutečně zlomilo. Předpokládejme, že deformace spočívá ve změně délky.
V tomto případě jsou napětí a deformace proporcionální, proto lze vzít v úvahu následující:
Pevnost ve smyku ∝ Deformace jednotky
Symbol ∝ znamená „úměrný“ a pokud jde o jednotkovou deformaci, je definována jako podíl mezi změnou délky, která se bude nazývat ΔL a původní délkou, zvanou Lnebo. Takto:
τ ∝ (ΔL / Lnebo)
Tažný modul
Protože jde o kvocient mezi dvěma délkami, kmen nemá žádné jednotky, ale při umístění symbolu rovnosti je musí poskytnout konstanta proporcionality. Volání G na uvedenou konstantu:
τ = G (ΔL / Lnebo)
G se volá tažný modul nebo řezací modul. Má jednotky Pascal v mezinárodním systému a jeho hodnota závisí na povaze materiálu. Tyto hodnoty lze určit v laboratoři testováním působení různých sil na vzorky různého složení..
Když je nutné určit velikost smykové síly z předchozí rovnice, stačí nahradit definici napětí:
τ = F / A = G (ΔL / Lnebo)
A jasné:
F = A × G (ΔL / Lnebo)
Smykové síly jsou velmi časté a jejich účinky je třeba vzít v úvahu v mnoha aspektech vědy a techniky. V konstrukcích se objevují v podpěrných bodech nosníků, mohou vzniknout při nehodě a zlomit si kost a jejich přítomnost je schopná změnit provoz strojů..
Působí ve velkém měřítku na zemskou kůru a díky tektonické činnosti způsobují zlomeniny hornin a geologické nehody. Proto jsou také zodpovědní za neustálé formování planety.
Reference
- Beer, F. 2010. Mechanika materiálů. 5. Edice. McGraw Hill. 7 - 9.
- Fitzgerald, 1996. Mechanika materiálů. Alfa Omega. 21-23.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mechanika materiálů. 6.. Edice. Pearson Education. 22-25
- Valera Negrete, J. 2005. Poznámky k obecné fyzice. UNAM. 87-98.
- Wikipedia. Smykové napětí. Obnoveno z: en.wikipedia.org.



Zatím žádné komentáře