
Bijektivní funkce co to je, jak se to dělá, příklady, cvičení

A bijektivní funkce je ten, který splňuje dvojí podmínku bytí injektivní a surjektivní. To znamená, že všechny prvky domény mají v codomainu jediný obrázek a na druhé straně se codomain rovná hodnosti funkce ( RF ).
Je splněno zvážením vztahu jedna k jedné mezi prvky domény a codomain. Jednoduchým příkladem je funkce F: R → R definovaný řádkem F (x) = x
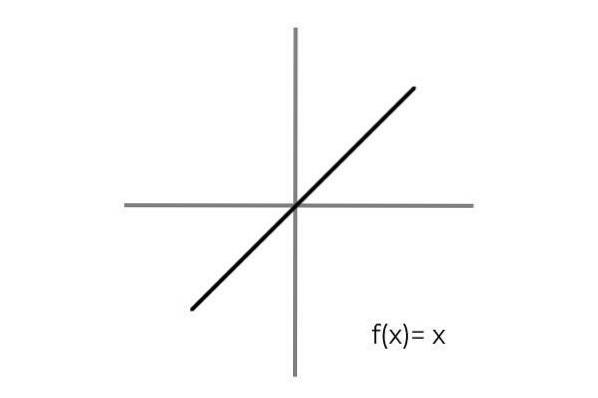
Je pozorováno, že pro každou hodnotu domény nebo výchozí sady (oba termíny platí stejně) je v sadě codomain nebo příjezdu jediný obraz. Kromě toho neexistuje žádný prvek codomain, který by nebyl obrazem.
Tím pádem F: R → R definovaný řádkem F (x) = x je bijective
Rejstřík článků
- 1 Jak provádíte bijektivní funkci?
- 1.1 Injektivita funkce
- 1.2 Surjektivita funkce
- 1.3 Podmínka funkce
- 2 Příklady: vyřešená cvičení
- 2.1 Cvičení 1
- 2.2 Cvičení 2
- 2.3 Cvičení 3
- 2.4 Cvičení 4
- 3 Navrhovaná cvičení
- 4 Odkazy
Jak děláte bijektivní funkci?
Abychom na to mohli odpovědět, je třeba si ujasnit pojmy, kterých se to týká Injektivita Y Surjektivita funkce, kromě kritérií pro podmínku funkcí za účelem jejich přizpůsobení požadavkům.
Injektivita funkce
Funkce je injekční když každý z prvků jeho domény souvisí s jediným prvkem codomain. Prvek codomain může být pouze obrazem jednoho prvku domény, tímto způsobem nelze opakovat hodnoty závislé proměnné.
Zvážit injekční k funkci musí být splněno následující:
∀ x1 ≠ xdva ⇒ F (x1 ) ≠ F (xdva )
Surjektivita funkce
Funkce je klasifikována jako surjektivní, pokud je každý prvek jeho codomainu obrazem alespoň jednoho prvku domény.
Zvážit surjektivní k funkci musí být splněno následující:
Být F: DF → CF
∀ b ℮ CF A do ℮ DF / F (a) = b
Toto je algebraický způsob, jak zjistit, že pro každé „b“, které patří CF existuje „a“, které patří D.F tak, že funkce vyhodnocená v „a“ se rovná „b“.
Podmínka funkce
Někdy funkce, která není bijektivní, může být vystaven určitým podmínkám. Tyto nové podmínky mohou způsobit, že bijektivní funkce. Platné jsou všechny druhy úprav domény a domény funkce, kde cílem je splnění vlastností injektivity a surjektivity v odpovídajícím vztahu..
Příklady: vyřešená cvičení
Cvičení 1
Nechte funkci F: R → R definovaný řádkem F (x) = 5x +1
A: [All real numbers]
Je pozorováno, že pro každou hodnotu domény je v codomainu obraz. Tento obrázek je jedinečný, což dělá F být injekční funkce. Stejným způsobem pozorujeme, že codomain funkce se rovná její hodnosti. Splňuje tedy podmínku surjektivita.
To, že jsme injektivní a surjektivní zároveň, můžeme z toho vyvodit
F: R → R definovaný řádkem F (x) = 5x +1 je bijektivní funkce.
To platí pro všechny lineární funkce (funkce, jejichž největší stupeň proměnné je jedna).
Cvičení 2
Nechte funkci F: R → R definován F (x) = 3xdva - dva
Při kreslení vodorovné čáry je možné pozorovat, že se graf nachází vícekrát. Z tohoto důvodu funkce F není to injektivní, a proto nebude bijektivní pokud je to definováno v R → R
Stejným způsobem existují hodnoty codomain, které nejsou obrazy žádného prvku domény. Z tohoto důvodu není funkce surjektivní, což si také zaslouží podmínit sadu příjezdu.
Pokračujeme v podmínění domény a domény funkce
F: [0 , ∞] → [- dva , ∞ ]
Kde je pozorováno, že nová doména zahrnuje hodnoty od nuly do kladného nekonečna. Vyhýbání se opakování hodnot, které ovlivňují injektivitu.
Podobně byla upravena codomain, která počítala od „-2“ do kladného nekonečna, což eliminovalo z codomain hodnoty, které neodpovídaly žádnému prvku domény
Tímto způsobem lze zajistit, že F : [0 , ∞] → [- dva , ∞ ] definován F (x) = 3xdva - dva
Je to bijektivní
Cvičení 3
Nechte funkci F: R → R definován F (x) = Sen (x)
V intervalu [ -∞ , +∞ ] sinusová funkce mění své výsledky mezi nulou a jednou.
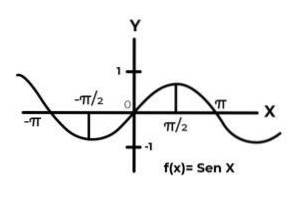
Funkce F neodpovídá kritériím injektivity a surjektivity, protože hodnoty závislé proměnné se opakují v každém intervalu π. Také podmínky codomain mimo interval [-elven] Nejsou obrazem žádného prvku domény.
Při studiu grafu funkce F (x) = Sen (x) jsou sledovány intervaly, kde chování křivky splňuje kritéria bijektivita. Jako například interval DF = [ π / 2,3π / 2 ] pro doménu. Y CF = [-1, 1] pro codomain.
Funkce se mění od 1 do -1 bez opakování jakékoli hodnoty v závislé proměnné. A zároveň se doména rovná hodnotám přijatým výrazem Sen (x)
Tímto způsobem funkce F: [ π / 2,3π / 2 ] → [-1, 1] definován F (x) = Sen (x). Je to bijektivní
Cvičení 4
Uveďte nezbytné podmínky pro DF a C.F. Takže výraz
F (x) = -xdva být bijektivní.
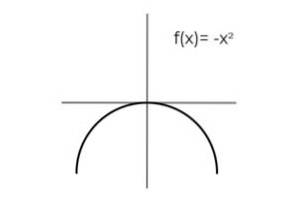
Opakování výsledků je pozorováno, když proměnná nabývá opačných hodnot:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
Doména je podmíněna a omezuje ji na pravou stranu skutečné linie.
DF = [0 , +∞ ]
Stejným způsobem je pozorováno, že rozsah této funkce je interval [ -∞ , 0], který při jednání jako codomain splňuje podmínky surjektivity.
Tímto způsobem můžeme dojít k závěru, že
Výraz F: [0 , +∞ ] → [ -∞ , 0] definován F (x) = -xdva Je to bijektivní
Navrhovaná cvičení
Zkontrolujte, zda jsou následující funkce bijektivní:
F: [0 , ∞) → R definován F (x) = 3 (x + 1)dva +dva
F: [ 3π / 2,5π / 2 ] → R. definován F (x) = 5 ctg (x)
F: [ -π,π ] → R. definován F (x) = Cos (x - 3)
F: R → R definovaný řádkem F (x) = -5x + 4
Reference
- Úvod do logiky a kritického myšlení. Merrilee H. Salmon. University of Pittsburgh
- Problémy v matematické analýze. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polsko.
- Prvky abstraktní analýzy. Mícheál O'Searcoid PhD. Katedra matematiky. University College Dublin, Beldfield, Dublind 4
- Úvod do logiky a metodologie dedukčních věd. Alfred Tarski, New York Oxford. Oxford University Press.
- Principy matematické analýzy. Enrique Linés Escardó. Redakční Reverté S. A 1991. Barcelona Španělsko.


Zatím žádné komentáře