Injekční funkce, co to je, k čemu to je a příklady

A injekční funkce je jakýkoli vztah prvků domény s jediným prvkem codomain. Také známý jako funkce jeden za druhým ( jedenáct ), jsou součástí klasifikace funkcí s ohledem na vztah jejich prvků.

Prvek codomain může být pouze obrazem jednoho prvku domény, tímto způsobem nelze opakovat hodnoty závislé proměnné.

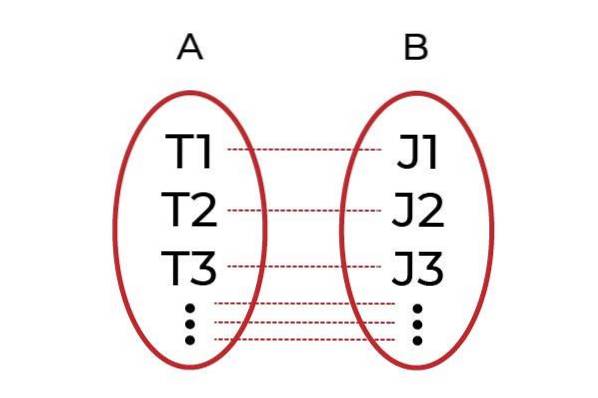
Jasným příkladem by bylo seskupení mužů s úlohami ve skupině A a ve skupině B všichni šéfové. Funkce F Bude to ten, který spojuje každého pracovníka se svým šéfem. Pokud je každý pracovník spojen s jiným šéfem prostřednictvím F, pak F  bude injekční funkce.

Zvážit injekční k funkci musí být splněno následující:

∀ x₁  ≠ x_dva   ⇒ F (x₁ ) ≠ F (x_dva )

Toto je algebraický způsob vyjádření Pro všechny x₁ odlišné od x_dva máte F (x₁ ) odlišné od F (x_dva ).

Rejstřík článků

• 1 K čemu slouží funkce vstřikování?
  • 1.1 Podmínka funkce
• 2 Příklady injekčních funkcí s vyřešenými cvičeními
  • 2.1 Příklad 1
  • 2.2 Příklad 2
  • 2.3 Příklad 3
  • 2.4 Příklad 4
  • 2.5 Příklad 5
  • 2.6 Příklad 6
  • 2.7 Příklad 7
• 3 Cvičení navržená pro třídu / domov
• 4 Odkazy

K čemu jsou injekční funkce?

Injektivita je vlastnost spojitých funkcí, protože zajišťují přiřazení obrázků pro každý prvek domény, což je základní aspekt v kontinuitě funkce..

Při kreslení čáry rovnoběžné s osou X na grafu injektivní funkce byste se měli dotknout grafu pouze v jednom bodě, bez ohledu na výšku nebo velikost Y čára je nakreslena. Toto je grafický způsob testování injektivity funkce.

Další způsob, jak otestovat, zda je funkce injekční, řeší pro nezávislou proměnnou X z hlediska závislé proměnné Y. Poté musí být ověřeno, zda doména tohoto nového výrazu obsahuje reálná čísla ve stejnou dobu jako pro každou hodnotu Y existuje jediná hodnota X.

Funkce nebo řádové vztahy se řídí mimo jiné notací F: D_F→C_F

Co se čte F běží od D_F až C._F

Kde je funkce F souvisí sady Doména Y Kodoména. Také se nazývá startovní a cílová sada.

Dominion D_F  obsahuje povolené hodnoty pro nezávislou proměnnou. Codomain C_F  Skládá se ze všech hodnot, které má závislá proměnná k dispozici. Prvky C_F související s D_F  jsou známé jako Rozsah funkcí (R._F ).

Podmínka funkce

Někdy může být funkce, která není injektivní, podrobena určitým podmínkám. Tyto nové podmínky mohou způsobit, že injekční funkce. Platí všechny druhy úprav domény a codomain funkce, kde cílem je splnění vlastností injektivity v odpovídajícím vztahu.

Příklady injekčních funkcí s vyřešenými cvičeními

Příklad 1

Nechte funkci F: R → R definovaný řádkem F (x) = 2x - 3

A: [All real numbers]

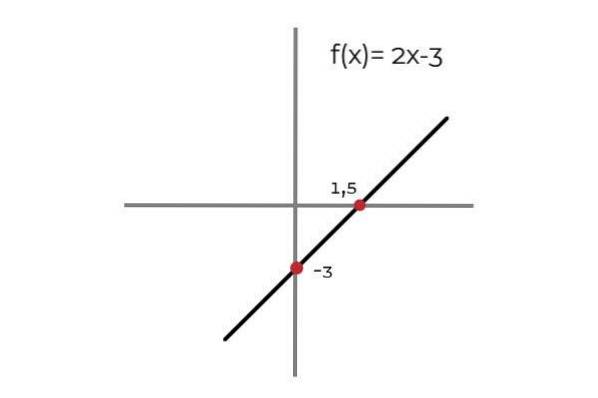
Je pozorováno, že pro každou hodnotu domény je v codomainu obraz. Tento obrázek je jedinečný, díky čemuž je F injekční funkcí. To platí pro všechny lineární funkce (funkce, jejichž největší stupeň proměnné je jedna).

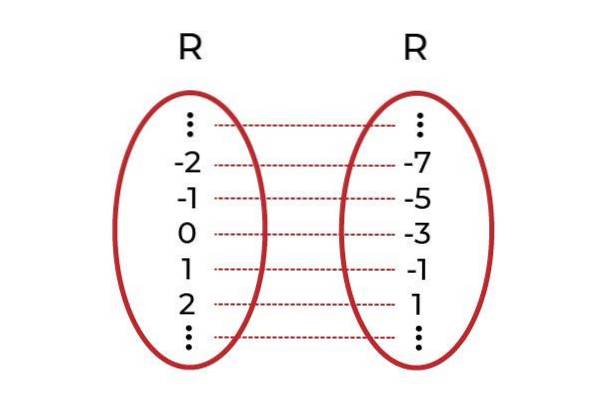
Příklad 2

Nechte funkci F: R → R definován F (x) = x^dva +1

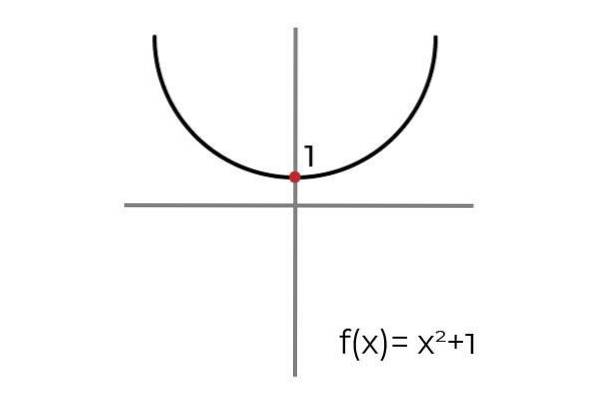
Při kreslení vodorovné čáry je možné pozorovat, že se graf nachází vícekrát. Z tohoto důvodu funkce F není to injektivní, pokud je to definováno  R → R

Pokračujeme k podmínce domény funkce:

                                               F: R⁺ NEBO 0 → R

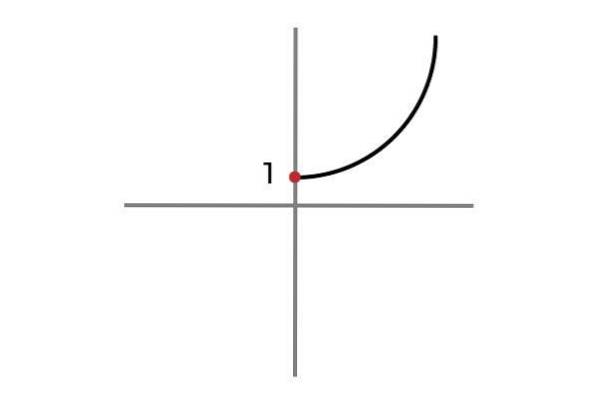
Nyní nezávislá proměnná nebere záporné hodnoty, tímto způsobem je zabráněno opakování výsledků a funkce F: R⁺ NEBO 0 → R definován F (x) = x^dva + 1 je injekční.

Dalším homologním řešením by bylo omezení domény doleva, to znamená omezení funkce tak, aby přijímala pouze záporné a nulové hodnoty.

Pokračujeme v podmínění domény funkce

                                               F: R^- NEBO 0 → R

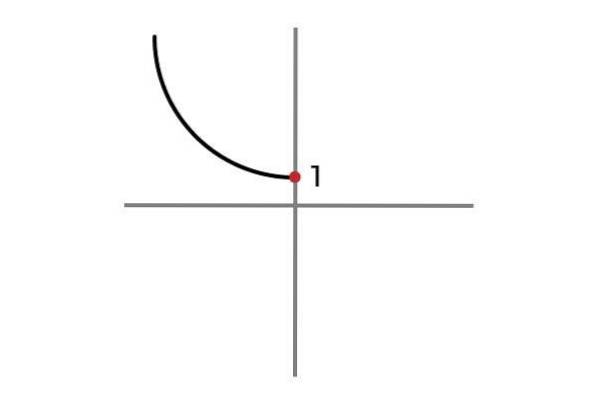
Nyní nezávislá proměnná nebere záporné hodnoty, tímto způsobem je zabráněno opakování výsledků a funkce F: R^- NEBO 0 → R definován F (x) = x^dva + 1 je injekční.

Trigonometrické funkce mají chování podobné vlnám, kde je velmi běžné najít opakování hodnot v závislé proměnné. Prostřednictvím specifického podmínění, založeného na předchozích znalostech těchto funkcí, můžeme zúžit doménu, abychom splnili podmínky injektivity.

Příklad 3

Nechte funkci F: [ -π / 2, π / 2 ] → R. definován F (x) = Cos (x)

V intervalu [ -π / 2 → π / 2 ] kosinová funkce mění své výsledky mezi nulou a jednou.

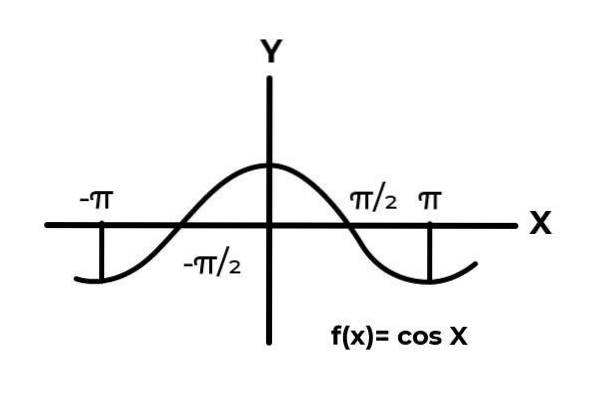
Jak je vidět na grafu. Začněte od nuly x = -π / 2 a poté dosáhne maxima na nule. Je po x = 0 že se hodnoty začnou opakovat, dokud se nevrátí na nulu x = π / 2. Tímto způsobem je známo, že F (x) = Cos (x) není injektivní pro interval [ -π / 2, π / 2 ] .

Při studiu grafu funkce F (x) = Cos (x) jsou sledovány intervaly, kdy se chování křivky přizpůsobuje kritériím injektivity. Jako například interval

[0 , π ]

Funkce se mění od 1 do -1 bez opakování jakékoli hodnoty v závislé proměnné.

Tímto způsobem funkce funkce F: [0 , π ] → R. definován F (x) = Cos (x). Je to injekční

Existují nelineární funkce, kde se vyskytují podobné případy. Pro výrazy racionálního typu, kde jmenovatel obsahuje alespoň jednu proměnnou, existují omezení, která zabraňují injektivitě vztahu.

Příklad 4

Nechte funkci F: R → R definován F (x) = 10 / x

Funkce je definována pro všechna reálná čísla kromě 0 kdo má neurčitost (Nelze jej dělit nulou).

Při přiblížení k nule zleva má závislá proměnná velmi velké záporné hodnoty a bezprostředně po nule mají hodnoty závislé proměnné velké kladné hodnoty.

Toto narušení způsobí výraz F: R → R definován F (x) = 10 / x

Nebuďte injekční.

Jak je vidět v předchozích příkladech, vyloučení hodnot v doméně slouží k „opravě“ těchto neurčitostí. Pokračujeme v vylučování nuly z domény a necháváme sady odletu a příjezdu definované takto:

R - 0 → R

Kde R - 0 symbolizuje reals s výjimkou sady, jejíž jediný prvek je nula.

Tímto způsobem výraz F: R - 0 → R definován F (x) = 10 / x je injektivní.

 Příklad 5

Nechte funkci F: [0 , π ] → R. definován F (x) = Sen (x)

V intervalu [0 , π ] sinusová funkce mění své výsledky mezi nulou a jednou.

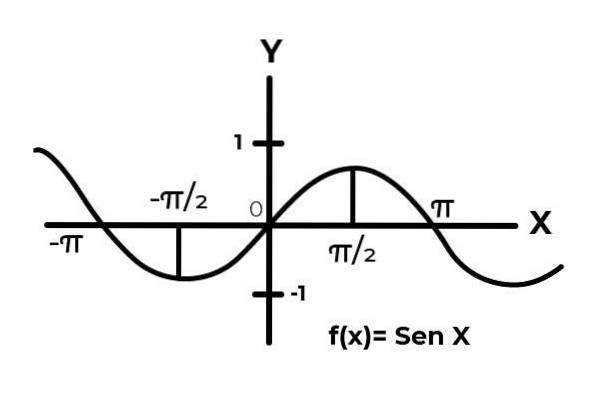
Jak je vidět na grafu. Začněte od nuly x = 0 poté dosáhne maxima v x = π / 2. Je po x = π / 2, že se hodnoty začnou opakovat, dokud se nevrátí na nulu x = π. Tímto způsobem je známo, že F (x) = Sen (x) není injektivní pro interval [0 , π ] .

Při studiu grafu funkce F (x) = Sen (x) jsou sledovány intervaly, kdy se chování křivky přizpůsobuje kritériím injektivity. Jako například interval  [  π / 2,3π / 2  ]

Funkce se mění od 1 do -1 bez opakování jakékoli hodnoty v závislé proměnné.

Tímto způsobem funkce F: [  π / 2,3π / 2  ] → R. definován F (x) = Sen (x). Je to injekční

Příklad 6

Zkontrolujte funkci F: [0, ∞) → R definován F (x) = 3x^dva je to injekční.

Tentokrát je doména výrazu již omezená. Rovněž je pozorováno, že hodnoty závislé proměnné se v tomto intervalu neopakují.

Lze tedy učinit závěr, že F: [0, ∞) → R definován F (x) = 3x^dva   je to injekční

Příklad 7

Určete, která z následujících funkcí je

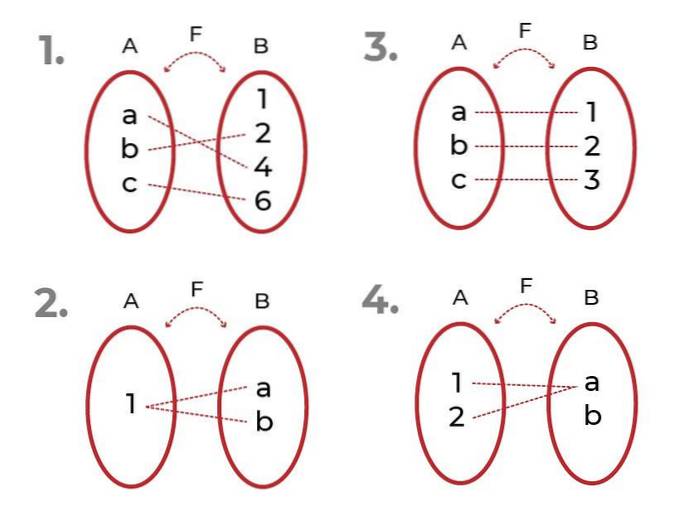
1. Je to injekční. Přidružené prvky codomain jsou jedinečné pro každou hodnotu nezávislé proměnné.
2. Není to injekční. Existují prvky codomain spojené s více než jedním prvkem výchozí sady.
3. Je to injekční
4. Není to injekční

Navrhovaná cvičení pro třídu / domov

Zkontrolujte, zda jsou následující funkce injektivní:

F: [0, ∞) → R definován F (x) = (x + 3)^dva  

F: [ π / 2,3π / 2  ] → R. definován F (x) = Tan (x)

F: [ -π,π  ] → R. definován F (x) = Cos (x + 1)

F: R → R definovaný řádkem F (x) = 7x + 2

Reference

1. Úvod do logiky a kritického myšlení. Merrilee H. Salmon. University of Pittsburgh
2. Problémy v matematické analýze. Piotr Biler, Alfred Witkowski. University of Wroclaw. Polsko.
3. Prvky abstraktní analýzy. Mícheál O'Searcoid PhD. Katedra matematiky. University College Dublin, Beldfield, Dublind 4.
4. Úvod do logiky a metodologie dedukčních věd. Alfred Tarski, New York Oxford. Oxford University Press.
5. Principy matematické analýzy. Enrique Linés Escardó. Redakční Reverté S. A 1991. Barcelona Španělsko.