Stupně volnosti, jak je vypočítat, typy, příklady

The stupně svobody ve statistikách je to počet nezávislých složek náhodného vektoru. Pokud má vektor n komponenty a tam jsou p lineární rovnice, které se vztahují k jejich složkám, pak stupeň svobody je n-p.

Koncept stupně svobody Také se objevuje v teoretické mechanice, kde zhruba odpovídá dimenzi prostoru, kde se částice pohybuje, minus počet vazeb..

Tento článek pojednává o konceptu stupňů volnosti aplikovaných na statistiku, ale mechanický příklad je snadnější vizualizovat v geometrické formě.

Rejstřík článků

• 1 Typy stupňů volnosti
  • 1.1 V mechanickém pouzdře
  • 1.2 V sadě náhodných hodnot
• 2 Příklady
  • 2.1 Rozptyl a stupně volnosti
  • 2.2 V distribuci chí kvadrát
  • 2.3 Při testování hypotéz (s vypracovaným příkladem)
• 3 Odkazy

Druhy stupňů volnosti

V závislosti na kontextu, ve kterém se používá, se způsob výpočtu počtu stupňů volnosti může lišit, ale základní myšlenka je vždy stejná: celkové rozměry minus počet omezení.

V mechanickém pouzdře

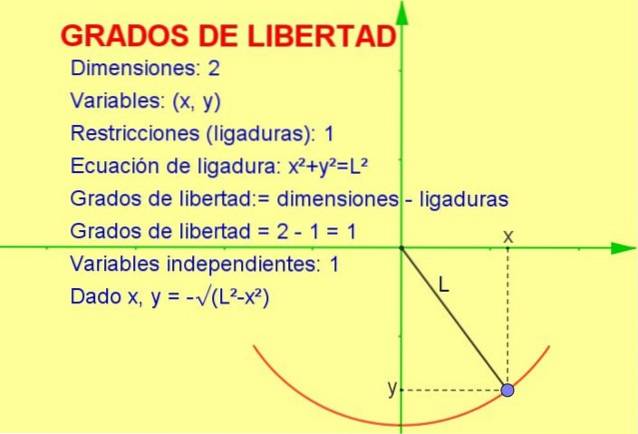
Uvažujme oscilační částici vázanou na strunu (kyvadlo), která se pohybuje ve svislé rovině x-y (2 rozměry). Částice je však nucena pohybovat se po obvodu poloměru rovnajícího se délce akordu.

Vzhledem k tomu, že se částice může pohybovat pouze na této křivce, počet stupně svobody je 1. To je vidět na obrázku 1.

Způsob výpočtu počtu stupňů volnosti spočívá v rozdílu počtu dimenzí minus počet omezení:

stupně volnosti: = 2 (rozměry) - 1 (ligatura) = 1

Další vysvětlení, které nám umožňuje dospět k výsledku, je následující:

-Víme, že poloha ve dvou dimenzích je reprezentována bodem souřadnic (x, y).

-Ale protože bod musí splňovat rovnici obvodu (x^dva + Y^dva = L^dva) pro danou hodnotu proměnné x je proměnná y určena uvedenou rovnicí nebo omezením.

Proto je pouze jedna z proměnných nezávislá a systém ji má jeden (1) stupeň volnosti.

V sadě náhodných hodnot

Pro ilustraci, co tento pojem znamená, předpokládejme vektor

X = (x₁, X_dva,..., X_n)

Co představuje vzorek n normálně distribuované náhodné hodnoty. V tomto případě náhodný vektor X mít n nezávislé komponenty, a proto se říká, že X mít n stupňů volnosti.

Nyní vytvořme vektor r odpadu

r = (x₁ - , X_dva - ,…., X_n - )

Kde představuje průměr vzorku, který se vypočítá takto:

= (x₁ + X_dva +…. + X_n) / n

Takže součet

(X₁ - ) + (x_dva - ) +…. + (X_n - ) = (x.)₁ + X_dva +…. + X_n) - n= 0

Je to rovnice, která představuje omezení (nebo vazbu) na prvky vektoru r zbytků, protože pokud je známo n-1 složek vektoru r, rovnice omezení určuje neznámou složku.

Proto vektor r dimenze n s omezením:

∑ (x_i - ) = 0

Mít (n - 1) stupňů volnosti.

Opět platí, že výpočet počtu stupňů volnosti je:

stupně volnosti: = n (rozměry) - 1 (omezení) = n-1

Příklady

Rozptyl a stupně volnosti

Variance s^dva je definován jako průměr druhé mocniny odchylek (nebo zbytků) vzorku n údajů:

s^dva = (r•r) / (n-1)

kde r je vektor zbytků r = (x1 - , x2 - ,…., Xn - ) a silný bod (•) je provozovatel skalárního produktu. Alternativně lze variantní vzorec napsat následovně:

s^dva = ∑ (x_i - )^dva / (n-1)

V každém případě je třeba poznamenat, že při výpočtu střední hodnoty čtverce zbytků se dělí (n-1), nikoli n, protože jak je uvedeno v předchozí části, počet stupňů volnosti vektor r je (n-1).

Pokud pro výpočet rozptylu byly vyděleny n místo (n-1) by výsledek měl zkreslení, které je velmi významné pro hodnoty n pod 50 let.

V literatuře se varianční vzorec také objevuje s dělitelem n místo (n-1), pokud jde o rozptyl populace.

Ale množina náhodné proměnné zbytků, představovaná vektorem r, Ačkoli má rozměr n, má pouze (n-1) stupňů volnosti. Pokud je však počet dat dostatečně velký (n> 500), oba vzorce konvergují ke stejnému výsledku.

Kalkulačky a tabulky poskytují obě varianty rozptylu a směrodatnou odchylku (což je druhá odmocnina rozptylu).

Naše doporučení, s ohledem na zde prezentovanou analýzu, je vždy zvolit verzi s (n-1) pokaždé, když je nutné vypočítat odchylku nebo směrodatnou odchylku, aby se zabránilo zkresleným výsledkům..

V distribuci chí kvadrát

Některá rozdělení pravděpodobnosti v spojité náhodné proměnné závisí na volaném parametru stupeň svobody, je případ chí kvadrát distribuce (χ^dva).

Název tohoto parametru pochází přesně ze stupňů volnosti podkladového náhodného vektoru, na který se toto rozdělení vztahuje.

Předpokládejme, že máme g populací, ze kterých se odebírají vzorky o velikosti n:

X₁ = (x1₁, x1_dva,… X1_n)

X2 = (x2₁, x2_dva,… X2_n)

... .

X_j = (xj₁, xj_dva,… Xj_n)

... .

Xg = (xg₁, xg_dva,… Xg_n)

Populace j co má průměr a směrodatná odchylka Sj, následuje normální rozdělení N (, Sj ).

Standardizovaná nebo normalizovaná proměnná zj_i je definován jako:

zj_i = (xj_i - ) / Sj.

A vektor Zj je definován takto:

Zj = (zj₁, zj_dva,..., zj_i,..., zj_n) a sleduje standardizované normální rozdělení N (0,1).

Takže proměnná:

Q = ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

následujte rozdělení χ^dva(g) volal chi square distribuce se stupněm volnosti G.

V testu hypotézy (s příkladem vypracován)

Chcete-li testovat hypotézy založené na určité sadě náhodných dat, musíte znát počet stupňů volnosti g aby bylo možné aplikovat test chí kvadrát.

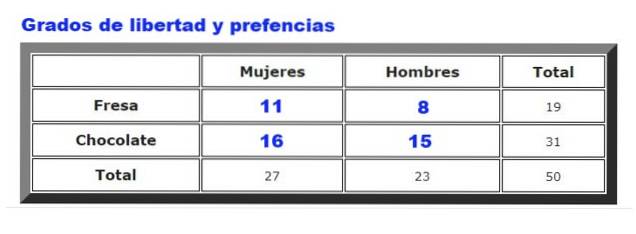
Jako příklad budou analyzovány údaje shromážděné o preferencích čokoládové nebo jahodové zmrzliny u mužů a žen v určitém zmrzlinovém salónu. Četnost, s jakou si muži a ženy volí jahody nebo čokoládu, je shrnuta na obrázku 2.

Nejprve se vypočítá tabulka očekávaných frekvencí, která se připraví vynásobením celkem řádků pro něj celkem sloupců, děleno celková data. Výsledek ukazuje následující obrázek:

Poté přistoupíme k výpočtu čtverce Chi (z údajů) pomocí následujícího vzorce:

χ^dva = ∑ (F._nebo - F_a)^dva / F._a

Kde F_nebo jsou pozorované frekvence (obrázek 2) a F_a jsou očekávané frekvence (obrázek 3). Součet jde přes všechny řádky a sloupce, které v našem příkladu obsahují čtyři výrazy.

Po provedení operací získáte:

χ^dva = 0,2043.

Nyní je nutné porovnat s teoretickým chí kvadrátem, který závisí na počet stupňů volnosti g.

V našem případě je toto číslo určeno následovně:

g = (# řádky - 1) (# sloupce - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Ukazuje se, že počet stupňů volnosti g v tomto příkladu je 1.

Pokud chcete zkontrolovat nebo odmítnout nulovou hypotézu (H0: neexistuje korelace mezi CHUŤEM a POHLAVÍ) s hladinou významnosti 1%, teoretická hodnota chí-kvadrát se počítá se stupněm volnosti g = 1.

Hledá se hodnota, která činí akumulovanou frekvenci (1 - 0,01) = 0,99, tj. 99%. Tato hodnota (kterou lze získat z tabulek) je 6,636.

Protože teoretická Chi překračuje vypočítanou, ověřuje se nulová hypotéza.

To znamená se shromážděnými údaji, Není pozorováno vztah mezi proměnnými CHUŤ a ROD.

Reference

1. Minitab. Jaké jsou stupně svobody? Obnoveno z: support.minitab.com.
2. Moore, David. (2009) Základní aplikované statistiky. Antoni Bosch editor.
3. Leigh, Jennifer. Jak vypočítat stupně volnosti ve statistických modelech. Obnoveno z: geniolandia.com
4. Wikipedia. Stupeň volnosti (statistika). Obnoveno z: es.wikipedia.com
5. Wikipedia. Stupeň volnosti (fyzická). Obnoveno z: es.wikipedia.com