Trigonometrické identity (příklady a cvičení)

The trigonometrické identity jsou vztahy mezi trigonometrickými poměry, které platí pro jakoukoli hodnotu proměnné. Například:

tan θ = sin θ / cos θ

Jedná se o trigonometrickou identitu, která spojuje tři poměry úhlu θ, tečny, sinu a kosinu uvedeného úhlu.

Tato identita platí pro všechny hodnoty, kromě těch, díky nimž je 0 jmenovatelem. Cos θ je 0 pro θ = ± π / 2, ± 3π / 2, ± 5π / 2… Dalším příkladem trigonometrické identity je:

hřích x. sec x. ctg x = 1

Rejstřík článků

• 1 Ukázka
• 2 Typy trigonometrických identit
  • 2.1 - Základní trigonometrické identity
  • 2.2 - Pythagorovy identity
  • 2.3 - Vzorce pro kosinus a sinus sčítání / odčítání úhlů
  • 2.4 - Vzorce pro dvojitý úhel
  • 2.5 - Vzorce pro poloviční úhel
• 3 Vyřešená cvičení
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
• 4 Odkazy

Demonstrace

Existují dva základní způsoby, jak ukázat, že trigonometrická identita je pravdivá:

1- Transformace jednoho z členů rovnosti na druhého pomocí pohodlných algebraických manipulací.

2 - Rozvíjejte samostatně oba členy rovnosti, dokud nebudou konečné výrazy každého z nich úplně stejné.

V navrhované identitě budeme transformovat levou stranu rovnosti, pro kterou vyjádříme ctg x a sec x z hlediska sinu a kosinu takto:

ctg x = cos x / sin x

sec x = 1 / cos x

Nahradíme tento výraz na levé straně identity a zjednodušíme:

hřích x. (1 / cos x). (cos x / sin x) = (sin x. cos x / cos x. sin x) = 1

A věrohodnost identity je již ověřena.

Typy trigonometrických identit

Existuje několik tříd trigonometrických identit. Níže stručně popíšeme ty hlavní:

- Základní trigonometrické identity

Rozlišujeme dva typy základních identit:

I) Ty, které jsou vyjádřeny základními poměry sinus, kosinus a tangenta:

• sec x = 1 / cos x
• cosec x / 1 / sin x
• ctg x = 1 / tg x
• tg x = sin x / cos x
• ctg x = cos x / sin x

II) Ty odvozené z parity. Z jeho grafu víme, že sin x je zvláštní funkce, což znamená, že:

sin (-x) = - sin x

Cos x je ze své strany sudá funkce, proto:

cos (-x) = cos x

Pak:

tg (-x) = sin (-x) / cos (-x) = -sen x / cos x

Podobně:

• cotg (-x) = -ctg x
• sec (-x) = sec x
• cosec (-x) = - cosec x

- Pythagorovy identity

Získávají se z aplikace Pythagorovy věty na pravý trojúhelník končetin a a b a přepony c. Uvidíme:

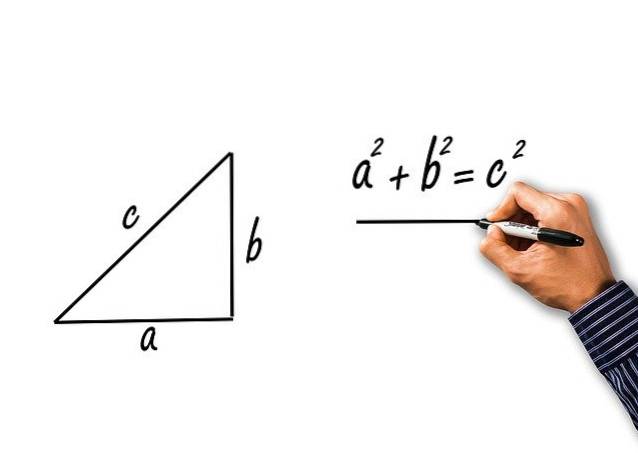
Pythagorova věta uvádí, že:

C^dva = a^dva + b^dva

Dělení všeho c^dva:

C^dva / c^dva = (a^dva / c^dva) + (B.^dva / c^dva)

Termín vlevo je 1 a pamatujeme si, že sinus a kosinus ostrého úhlu α jsou definovány jako:

sin α = a / c

cos α = b / c

Výsledek:

1 = (hřích α)^dva + (cos α)^dva

Tato identita je známá jako základní identita.

Postup lze provést vydělením a^dva a b^dva, což vede k dalším dvěma identitám:

sek^dva α = 1 + tg^dva α

sklizeň^dva α = 1 + ctg^dva α

- Vzorce pro kosinus a sinus sčítání / odčítání úhlů

Hlavní trigonometrické identity pro kosinus, sinus a tečnu sčítání a odčítání jsou následující:

Důkaz hříchu (α + β) a cos (α + β)

Tyto identity lze prokázat geometricky nebo také podle Eulerova vzorce:

a^iα = cos α + i sin α

Podívejme se, co se stane s vzorcem, když dosadíme součet dvou úhlů α a β:

a^{i (α +β)} = cos (α + β) + i sin (α + β)

Tento výraz je složitý, jeho skutečná část je cos (α + β) a jeho imaginární část je i sin (α + β). Tento výsledek uložíme pro pozdější použití a zaměříme se na vývoj exponenciální části:

a^{i (α +β)} = e^iα ⋅ e^iβ = (cos α + i sin α). (cos β + i sin β) =

= cos α⋅cos β + cos α⋅i sin β + i⋅sen α cos β - sin α⋅sen β

Skutečná část tohoto výrazu je ta, která není vynásobena imaginární jednotkou „i“:

cos α⋅cos β - sin α. hřích β

Pomyslná část tedy je:

i (cos α⋅sen β + sin α⋅cos β)

Aby byly dva složité výrazy stejné, musí se skutečná část jednoho rovnat skutečné části druhého. Totéž se děje s imaginárními částmi.

Vezmeme uložený výsledek a porovnáme ho s tímto:

cos α. cos β - sin α. sin β = cos (α + β)

i (cos α⋅sen β + sin α⋅cos β) = i sin (α + β)

sin (α + β) = (cos α. sin β + sin α⋅cos β)

- Vzorce pro dvojitý úhel

V předchozích vzorcích bereme β = α a vyvíjíme:

sin (α + α) = sin 2 α = sin α⋅cos α + cos α. sin α = 2⋅ sin α ⋅ cos α

cos (α + α) = cos 2 α = cos α⋅cos α - sin α⋅sen α = cos^dva α - hřích ^dva α

tg (α + α) = tg 2 α = [tg α + tg α] / [1- tg α⋅tg α] = 2tg α / 1- tg^dva α

Pokud ve druhém výrazu dosadíme cos^dva α = 1 - hřích^dva α se získá:

cos 2 α = cos^dva α - (1- cos^dva α) = 2 cos^dva α -1

- Vzorce pro poloviční úhel

V tomto posledním výrazu, pojďme dosadit α za α / 2, zůstane následující:

cos α = 2 cos ^dva(α / 2) -1

Řešení pro:

Vyřešená cvičení

- Cvičení 1

Ukaž to:

Levý termín budeme pracovat algebraicky tak, aby vypadal jako pravý. Protože sin x se objevuje ve správném termínu, je prvním krokem vyjádření cos^dvax z hlediska hříchu x, takže vše je ve stejném trigonometrickém poměru:

Pak je započítán 1 - hřích^dva x, protože to je rozdíl dokonalých čtverců. Za tímto účelem vymaže základní identitu:

cos^dvax = 1 - hřích^dva X

1 - sen^dva x = (1- sin x) (1 + sinx)

A faktorizace je nahrazena původním výrazem:

Termín (1 - sinx) je zjednodušený a zůstává zachována rovnost:

1 + hřích x = 1 + hřích

- Cvičení 2

Vyřešte následující trigonometrickou rovnici a uveďte řešení pro hodnoty mezi 0 a 360 °:

tg x + s^dva x = 3

Řešení

V pojmu vlevo jsou dva trigonometrické poměry, proto je nutné vše redukovat na jediný, aby bylo možné vyřešit neznámé. Pojem sek^dva x je vyjádřeno prostřednictvím jedné z Pythagorovských identit:

sek^dva α = 1 + tg^dva α

Dosazení do rovnice zůstává:

tg x + 1 + tg^dva x = 3

Přeskupení podmínek:

tg^dva x + tg x + 1 = 3

Tato rovnice je řešena provedením změny proměnné:

tg x = u

nebo^dva + u + 1-3 = 0 → u^dva + u - 2 = 0

Tuto kvadratickou rovnici lze snadno vyřešit pomocí factoringu:

(u +2) (u-1) = 0

Proto u₁ = -2 a u_dva = 1, což odpovídá:

tg x₁ = -2

tg x_dva = 1

Konečně:

X₁ = arctg (-2) = 296,6 °

X_dva  = arctg (1) = 45 °

Reference

1. Carena, M. 2019. Pre-University Matematická příručka. Národní univerzita v Litoralu.
2. Figuera, J. 1999. Mathematics. 1. místo Diverzifikovaný. Bolivarian Collegiate Edition.
3. Hoffman, J. Výběr témat matematiky. Svazek 4.
4. Jiménez, R. 2008. Algebra. Hala Prentice.
5. Wikipedia. Identity a vzorce trigonometrie. Obnoveno z: es.wikipedia.org.
6. Zapata, F. 4 způsoby řešení kvadratické rovnice. Obnoveno z: francesphysics.blogspot.com.
7. Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.