
Hookovy zákony, příklady, aplikace, cvičení
The Hookeův zákon poukazuje na to, že deformace elastického předmětu je přímo úměrná síle, která na něj působí. Konstanta proporcionality závisí na povaze objektu, jeho geometrii a materiálu, ze kterého je vyroben..
Všechny materiály mají ve větší či menší míře elastické vlastnosti, takže vyhovují Hookovu zákonu, pokud se vrátí do svých původních rozměrů, jakmile síla přestane. Pružiny a gumičky jsou dobrým příkladem předmětů, které splňují Hookeův zákon, ale stejně tak i ocelové čepy, které jsou součástí mostu.

Vezmeme-li jako příklad pružinu nebo pružinu, aby bylo možné ji udržovat napnutou nebo stlačenou, je nutné použít sílu, jejíž velikost je F. Podle Hookeova zákona bude pružina zažívat deformaci x:
F ∝ x
Konstanta proporcionality, kterou je pružina, se nazývá konstanta tuhosti pružiny, se označuje jako k, proto:
F = k⋅x
V jednotkách mezinárodního systému je síla v newtonech (N) a deformace v metrech (m). Proto má konstanta pružiny jednotky N / m. Konstanta pružiny představuje sílu, která musí být použita k jejímu deformování o délku 1 m.
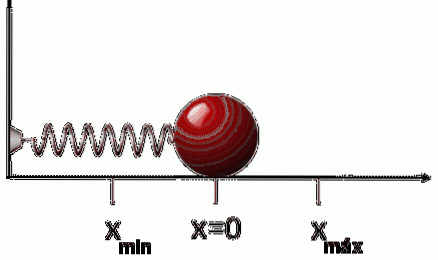
Pokud se pružina po roztažení nebo stlačení uvolní, bude se pohybovat v opačném směru, než je použitá síla. To znamená, že pokud jej natáhneme, stlačí se a naopak. Proto síla FR co pružina působí to je:
FR = -k⋅x
Záporné znaménko znamená výše uvedené: že síla je proti posunutí, proto je tato síla známá jako regenerační síla.
Rejstřík článků
- 1 Vzorec a rovnice
- 1.1 Práce natahovaná nebo stlačovaná na pružině
- 2 Příklady pružin
- 2.1 Přítlačná pružina
- 2.2 Tažné a torzní pružiny
- 2.3 Materiály pro výrobu pružin
- 3 Aplikace Hookova zákona
- 4 Vyřešená cvičení
- 4.1 - Cvičení 1
- 4.2 - Cvičení 2
- 5 Reference
Vzorec a rovnice
Vztah mezi silou a posunem na jaře objevil Robert Hooke (1635-1703), významný anglický fyzik známý svou rivalitou s Isaacem Newtonem. Hooke byl všestranný vědec, který se úspěšně pustil do různých vědních oblastí: mechaniky, biologie, astronomie a architektury..

Hooke si uvědomil, že pokud síla působící na pružinu není příliš velká, pružina se deformuje úměrně síle a jakmile tato síla zmizí, pružina se vrátí do své přirozené délky.
Takže Hookeův zákon v grafické podobě má tvar přímky, jejíž sklon je konstanta pružiny. Následující obrázek ukazuje sílu působící na pružinu, aby ji natáhla - nebo stlačila - jako funkce polohy x. Všimněte si také, že síla nezávisí na přirozené délce pružiny, ale na jejím posunutí..
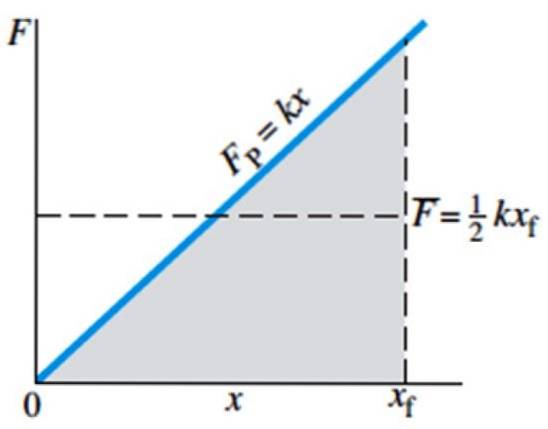
Průměrná síla je na grafu vyznačena sloupcem F a rovná se ½ kxF, kde xF je konečná poloha pružiny.
Jak síla působící na pružinu, tak síla, kterou působí na předmět s ní spojený, jsou proměnné síly. Čím více chcete pružinu natáhnout nebo stlačit, tím větší sílu musíte použít, abyste toho dosáhli..
Práce na roztažení nebo stlačení pružiny
Když je na pružinu aplikována deformační síla, je provedena práce, která je uložena v pružině a může být použita později..
Mechanická práce je definována jako plocha pod grafem síly F jako funkce polohy x. Pro výpočet práce W, kterou proměnná síla F (x) působí při pohybu objektu z polohy x1 až do polohy xdva musíme vypočítat určitý integrál:
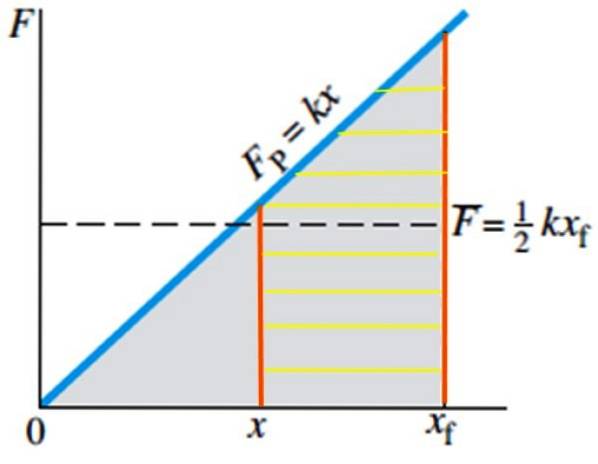
V případě práce potřebné k uvedení pružiny z její rovnovážné polohy do polohy xF Je to velmi jednoduché, protože oblast, která se má vypočítat, je plocha trojúhelníku šedě na obrázku 4, jehož vzorec je známý:
Plocha trojúhelníku = ½ základny. výška
Proto je nutná práce:
W = ½ xF . (kxF) = ½ k (x.)F)dva
A pokud chcete vypočítat práci potřebnou k uvedení pružiny z polohy x do polohy xF, by odpovídalo výpočtu plochy šrafovaného lichoběžníku na obrázku 5:
W = ½ k (xF)dva - ½ k xdva

Příklady pružin
V závislosti na aplikaci, pro kterou jsou určeny, mohou být pružiny šroubovité, válcové, kónické, spirálové, s kruhovým průřezem (nejběžnější), čtvercové nebo obdélníkové..
Široce používaná klasifikace je podle typu úsilí, kterému budou vystaveni: existují torzní, flexe, tlačné a tažné pružiny. Ty jsou hojně používány a některé fungují stejně pro napětí a kompresi..
Kompresní pružina
Příkladem tlačné pružiny je pružina použitá v hračce zvané pogo nebo skákací hůl. Tyto pružiny ukládají spoustu potenciální energie, když jsou stlačeny, a uvolňují ji kousek po kousku, když se vracejí do rovnovážné polohy. Tímto způsobem nejsou odskoky příliš prudké.

Tažné a torzní pružiny
Trampolínové pružiny jsou typu tažných pružin a jsou vyráběny s pevně navinutými vinutími, se dvěma háčky na koncích. Jsou schopni zadržet spoustu potenciální energie, kterou pak uvolní, když někdo vyleze a začne skákat po podložce, která má stejně jako všechny materiály svou vlastní pružnou odezvu..
Torzní pružiny jsou velmi běžné, protože se používají k výrobě kolíků na prádlo. Namísto háčků na koncích se ohýbají pod úhlem, aby odolávaly torzním silám.

Materiály pro výrobu pružin
Nejvhodnější materiály pro výrobu pružin jsou materiály s a konečný odpor (konečný odpor) vysoký, to znamená, že podporují velké úsilí před zlomením. Je také žádoucí, aby materiál měl vysokou mez kluzu, aby při malém úsilí neztratil své elastické vlastnosti..
Těžké pružiny jsou vyrobeny ze slitin, včetně vysoce uhlíkové oceli, mědi, niklu a bronzu.
Hooke's Law Applications
Jelikož pružiny mají schopnost akumulovat potenciální energii, když jsou natažené nebo stlačené, jsou schopné dělat práci pohybováním věcí, jako jsou mechanismy..
Tímto způsobem mají pružiny mnoho využití, od malých a každodenních předmětů, přes automobily, až po stroje všeho druhu. Pružiny se používají k:
-Tlumte vibrace.
-Výroba zatahovacích mechanismů: pera, kolíčky na prádlo, sponky do vlasů.
-Vyrobte si pružinové váhy nebo dynamometry
A jsou také součástí mechanismu:
-Hodiny.
-Trampolíny.
-Zámky.
-Hračky.
-Zbraně.
-Jehlové měřiče, například galvanometr, se používají k měření proudů, napětí a odporů.
Vyřešená cvičení
- Cvičení 1
Na pružinu působí síla o velikosti 5,0 N, což způsobí, že se z její přirozené délky natáhne délka 3,5 cm..
a) Kolik se natáhne, když je aplikovaná síla 7 N.?
b) Najděte práci vynaloženou silou na natažení pružiny 3,5 cm od její přirozené délky.
Řešení
S vědomím, že pružina je natažena 3,5 cm působením 5,0 N, můžeme vypočítat její konstantu:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Při použití síly 7 N se získá následující protažení:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Řešení b
Práce potřebná k deformaci pružiny je dána:
W = ½ kxdva = 0,5 x 1,43 N / cm x (3,5 cm)dva = 8,76 N. cm = 8,76 N. 1 x 10 -dva m = 0,0876 J.
- Cvičení 2
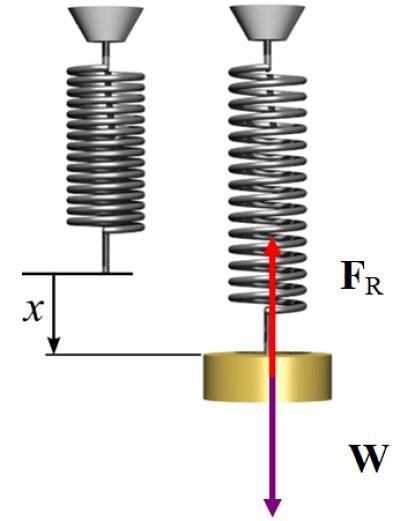
Z podpěry je zavěšen pramen zanedbatelné hmotnosti a dlouhý 10 cm. Pokud je na něj zavěšena 2 kg hmota, pružina se natáhne na 15 cm. Vypočítat:
a) Konstanta pružiny
b) Velikost pružiny, když je zavěšena hmotnost 3 kg.
Řešení
Roztažení pružiny je x = 15 - 10 cm = 5 cm
Jelikož je systém ve statické rovnováze, síla vyvíjená pružinou při protahování je směrována svisle nahoru, aby se vyrovnala váha, která je směrována dolů, poté:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x 10 -dva m = 392 N / m
Řešení b
Když je zavěšeno 3 kg závaží, nová síla je W = 3 x 9,8 N = 29,4 N
V takovém případě je úsek:
x = mg / k = 29,4 N / 392 N / m = 0,075 m = 7,5 cm
Reference
- Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
- Blog kreativních mechanismů. Čtyři různé typy pružin. Obnoveno z: creativemechanisms.com.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 2. Dynamika. Upravil Douglas Figueroa (USB).
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Ed. Prentice Hall.
- .



Zatím žádné komentáře