Míry polohy, centrální tendence a rozptylu

The míry centrální tendence, rozptylu a polohy, jsou hodnoty, které se používají ke správné interpretaci souboru statistických údajů. S nimi lze pracovat přímo, protože jsou získány ze statistické studie, nebo mohou být uspořádány do skupin se stejnou frekvencí, což usnadňuje analýzu..

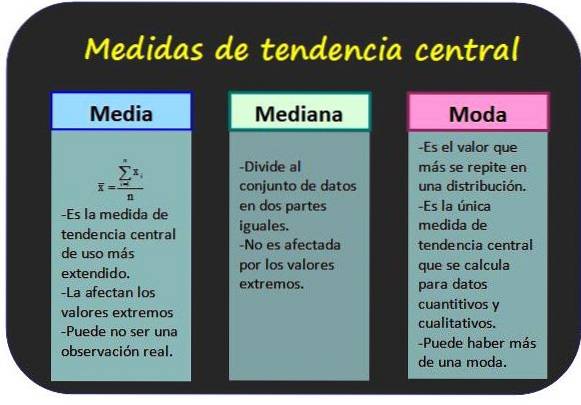
Opatření centrální tendence

Umožňují vědět, kolem kterých hodnot jsou statistické údaje seskupeny.

Aritmetický průměr

Je také znám jako průměr hodnot proměnné a je získán sečtením všech hodnot a vydělením výsledku celkovým počtem dat.

• Aritmetický průměr pro seskupená data

Nechť je proměnná x, jejíž máme n dat bez organizování nebo seskupování, její aritmetický průměr se vypočítá takto:

A v součtu notace:

Příklad

Majitelé horského turistického hostince mají v úmyslu vědět, kolik dní v průměru zůstávají návštěvníci v zařízeních. K tomu byl veden záznam o dnech trvalosti 20 skupin turistů, přičemž byly získány následující údaje:

1; 1; dva; dva; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; dva; dva; 3; 4; 1

Průměrný počet dnů pobytu turistů je:

• Aritmetický průměr pro seskupená data

Pokud jsou data proměnné uspořádána do tabulky absolutních frekvencí f_i a třídní centra jsou x₁, X_dva,..., X_n, průměr se vypočítá podle:

V součtu notace:

Medián

Medián skupiny n hodnot proměnné x je centrální hodnotou skupiny za předpokladu, že jsou hodnoty seřazeny ve vzestupném pořadí. Tímto způsobem je polovina všech hodnot menší než režim a druhá polovina je větší..

• Medián neseskupených dat

Mohou nastat následující případy:

-Počet n hodnot proměnné x  zvláštní: medián je hodnota, která je přímo uprostřed skupiny hodnot:

-Počet n hodnot proměnné x pár: v tomto případě se medián vypočítá jako průměr dvou centrálních hodnot datové skupiny:

Příklad

Chcete-li zjistit medián dat z turistické ubytovny, jsou nejprve seřazeny od nejnižší po nejvyšší:

1; 1; 1; 1; 1; 1; 1; dva; dva; dva; dva; 3; 3; 3; 4; 4; 4; 4; 5; 5

Počet dat je sudý, proto existují dvě centrální data: X₁₀ a X_jedenáct a protože oba mají hodnotu 2, jejich průměr je také.

Medián = 2

• Medián sdružených dat

Používá se následující vzorec:

Symboly ve vzorci znamenají:

-c: šířka intervalu, který obsahuje medián

-B_M: dolní mez stejného intervalu

-F_m: počet pozorování obsažených v intervalu, ke kterému medián patří.

-n: celková data.

-F_BM: počet pozorování před intervalu obsahujícího medián.

móda

Režim pro seskupená data je hodnota s nejvyšší frekvencí, zatímco pro seskupená data je to třída s nejvyšší frekvencí. Móda je považována za nejreprezentativnější data nebo třídu distribuce.

Dvě důležité charakteristiky tohoto opatření spočívají v tom, že soubor dat může mít více než jeden režim a režim lze určit pro kvantitativní i kvalitativní data..

Příklad

Při pokračování v datech turistického paradoru se nejvíce opakuje číslo 1, proto je nejběžnější věcí to, že turisté zůstanou v paradoru 1 den.

Míra disperze

Míra rozptylu popisuje, jak jsou seskupena data kolem centrálních měřítek.

Hodnost

Vypočítává se odečtením největších a nejmenších dat. Pokud je tento rozdíl velký, je to znamení, že data jsou rozptýlena, zatímco malé hodnoty označují, že data jsou blízko průměru..

Příklad

Rozsah údajů turistického paradora je:

Rozsah = 5−1 = 4

Rozptyl

• Odchylka pro seskupená data

Chcete-li najít rozptyl s^dva Je nutné nejprve znát aritmetický průměr, poté se vypočítá čtvercový rozdíl mezi každou částí dat a průměrem, všechny se sečtou a vydělí celkovým počtem pozorování. Tyto rozdíly jsou známé jako odchylky.

Rozptyl, který je vždy kladný (nebo nulový), ukazuje, jak daleko jsou pozorování od průměru: pokud je rozptyl vysoký, jsou hodnoty rozptýlenější, než když je rozptyl malý.

Příklad

Rozptyl údajů z turistické ubytovny je:

1; 1; dva; dva; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; dva; dva; 3; 4; 1

• Odchylka pro seskupená data

K nalezení rozptylu seskupené datové sady jsou zapotřebí následující: i) průměr, ii) frekvence f_i  což je celkový údaj v každé třídě a iii) x_i  nebo hodnota třídy:

Směrodatná odchylka je kladná druhá odmocnina rozptylu, takže má oproti rozptylu výhodu: přichází ve stejných jednotkách jako studovaná proměnná, takže máte přímější představu o tom, jak blízko nebo daleko je proměnná z průměru.

• Směrodatná odchylka pro seskupená data

Určuje se jednoduše nalezením druhé odmocniny rozptylu pro seskupená data:

Standardní odchylka pro údaje z turistické ubytovny je:

s = √ (s^dva) = √ 1,95 = 1,40

• Směrodatná odchylka pro seskupená data

Vypočítá se tak, že se najde druhá odmocnina rozptylu pro seskupená data:

Měření polohy

Míry polohy rozdělují uspořádanou sadu dat na kousky stejné velikosti. Medián, kromě toho, že je měřítkem centrální tendence, je také měřítkem pozice, protože rozděluje celek na dvě stejné části. Ale menší části lze získat kvartily, decily a percentily.

Kvartily

Kvartily rozdělují sadu na čtyři stejné části, z nichž každá obsahuje 25% dat. Jsou označeny jako Q₁, Q_dva a Q₃ a medián je kvartil Q_dva. Tímto způsobem je 25% dat pod Q kvartilem.₁, 50% pod Q kvartil_dva nebo medián a 75% pod Q kvartil₃.

• Kvartily pro seskupená data

Data jsou uspořádána a celková částka je rozdělena do 4 skupin se stejným počtem dat. Pozici prvního kvartilu najde:

Q₁ = (n + 1) / 4

Kde n jsou celková data. Pokud je výsledkem celé číslo, jsou umístěna data odpovídající této poloze, ale pokud jsou desetinná, jsou data odpovídající celočíselné části zprůměrována s dalším, nebo pro větší přesnost jsou lineárně interpolována mezi uvedenými daty.

Příklad

Pozice prvního kvartilu Q₁ pro údaje turistického paradora je:

Q₁ = (n + 1) / 4 = (20 + 1) / 4 = 5,25

Toto je poloha kvartilu 1 a protože výsledek je desítkový, prohledají se data X.₅ a X_6, což jsou příslušně X₅ = 1 a X₆ = 1 a jsou zprůměrovány, což má za následek:

První kvartil = 1

1; 1; 1; 1; 1; 1; 1; dva; dva; dva; dva; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Pozice druhého kvartilu Q_dva to je:

Q_dva = 2 (n + 1) / 4 = 10,5

Jaký je průměr mezi X₁₀ a X_jedenáct a odpovídá mediánu:

Druhý kvartil = Medián = 2

Pozice třetího kvartilu se vypočítá podle:

Q₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75

Je také desítkové, proto se průměruje X_patnáct a X₁₆:

1; 1; 1; 1; 1; 1; 1; dva; dva; dva; dva; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Ale protože oba mají hodnotu 4:

Třetí kvartil = 4

Obecný vzorec pro umístění kvartilů v neseskupených datech je:

Q_k = k (n + 1) / 4

S k = 1,2,3.

• Kvartily pro seskupená data

Počítají se podobným způsobem jako medián:

Vysvětlení symbolů je:

-B_Q: spodní hranice intervalu obsahujícího kvartil

-c: šířka tohoto intervalu

-F_co: počet pozorování obsažených v kvartilovém intervalu.

-n: celková data.

-F_BQ: počet dat před intervalu obsahujícího kvartil.

Decily a percentily

Decilly a percentily rozdělují soubor dat na 10 stejných částí a 100 stejných částí a jejich výpočet se provádí podobným způsobem jako u kvartilů.

• Deciles a percentily pro seskupená data

Používají se vzorce:

D_k = k (n + 1) / 10

S k = 1,2,3… 9.

Decile D₅ se musí rovnat mediánu.

P_k = k (n + 1) / 100

S k = 1,2,3… 99.

Percentil P_padesátka se musí rovnat mediánu.

Příklad

V příkladu turistické ubytovny je poloha D.₃ to je:

D₃ = 3 (20 + 1) / 10 = 6,3

Protože se jedná o desítkové číslo, X se zprůměruje₆ a X_7, obě rovny 1:

1; 1; 1; 1; 1; 1; 1; dva; dva; dva; dva; 3; 3; 3; 4; 4; 4; 4; 5; 5

To znamená, že 3 desetiny dat jsou pod X₇ = 1 a zbývající výše.

• Decily a percentily pro seskupená data

Vzorce jsou analogické vzorcům pro kvartily. D se používá k označení decilů a P pro percentily a symboly se interpretují podobně:

Empirické pravidlo

Když jsou data symetricky distribuována a distribuce je unimodální, existuje pravidlo s názvem  empirické pravidlo nebo pravidlo 68 - 95 - 99, který je seskupuje v následujících intervalech:

• 68% dat je v rozsahu:

• 95% dat je v rozsahu:

• 99% dat je v rozsahu:

Příklad

V jakém intervalu je 95% údajů od turistického paradora?

Jsou v intervalu: [2,5–1,40; 2,5 + 1,40] = [1,1; 3,9].

Reference

1. Berenson, M. 1985. Statistiky pro management a ekonomiku. Interamericana S.A.
2. Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
3. Levin, R. 1988. Statistiky pro správce. 2. místo Edice. Hala Prentice.
4. Spiegel, M. 2009. Statistiky. Série Schaum. 4. místo Edice. Mcgraw kopec.
5. Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.