The moment hybnosti nebo moment hybnosti je pro rotační pohyb to, co je lineární hybnost pro translační pohyb. Jedná se o vektorovou veličinu, která charakterizuje rotaci bodové částice nebo objektu rozšířeného kolem osy, která prochází bodem.
To znamená, že kdykoli se má vypočítat moment hybnosti, musí být odpovídajícím způsobem specifikována osa otáčení.
Počínaje hmotným bodem hmotnosti m je moment hybnosti označen L, lineární hybnost jako p a poloha částice vzhledem k ose, která prochází určitým bodem O je r, pak:
L = r X p
Tučná písmena jsou vyhrazena pro vektorové veličiny a kříž znamená, že moment hybnosti je vektorovým součinem mezi pozičním vektorem r a lineární moment p částice. Vektor, který je výsledkem vektorového produktu, je kolmý k rovině tvořené zúčastněnými vektory.
To znamená, že směr a smysl pro L lze najít pomocí pravidla pravé ruky pro křížový produkt.
V mezinárodním systému jednotek SI jsou jednotky momentu hybnosti kg⋅mdva/ s, které nemají speciální název. A pro rozšířené tělo, které se skládá z mnoha částic, se výše uvedená definice pohodlně rozšíří.
Rejstřík článků
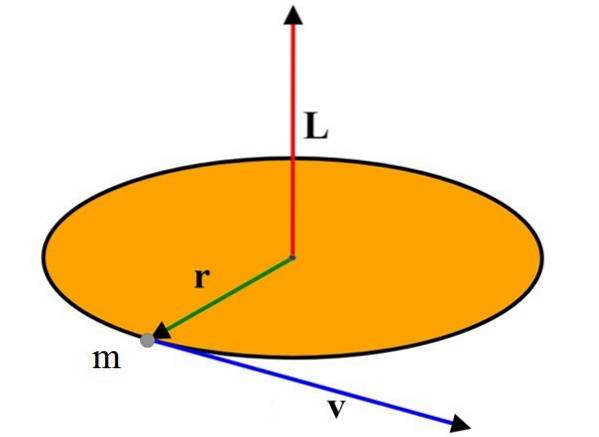
Velikost vektoru momentu hybnosti je podle definice vektorového produktu:
L = r⋅m⋅v⋅sen ϕ = mv (r⋅sen ϕ) = mvℓ
Kde ϕ je úhel mezi vektory r Y proti. Pak ℓ = r sin ϕ je kolmá vzdálenost mezi přímkou proti a bod O.
V případě částice, která se pohybuje a popisuje obvod zobrazený na horním obrázku, je tento úhel 90 °, protože rychlost je vždy tečná k obvodu, a proto kolmá k poloměru..
Proto hřích 90º = 1 a velikost L to je:
L = m⋅r⋅v
Moment setrvačnosti tuhého tělesa popisuje setrvačnost tělesa proti rotaci kolem určité osy.
Závisí to nejen na hmotnosti těla, ale také na vzdálenosti k ose otáčení. To je snadno pochopitelné, když si myslíte, že u některých objektů je snazší otáčet se kolem některých os než u jiných..
U soustavy částic je moment setrvačnosti, označený písmenem I, dán vztahem:
I = ∑ ridva Δmi
Kde Δmi je malá část těsta a ri je jeho vzdálenost od osy otáčení. Rozšířené tělo se skládá z mnoha částic, proto je jeho celkový moment setrvačnosti součtem všech produktů mezi hmotou a vzdáleností částic, které jej tvoří..
Pokud se jedná o rozšířené tělo, součet se změní na integrální a Δm se stává hmotnostním rozdílem dm. Limity integrace závisí na geometrii objektu:
I = ∫M (rdva) dm
Koncept momentu setrvačnosti úzce souvisí s momentem hybnosti rozšířeného objektu, jak uvidíme níže.
Uvažujme soustavu částic složenou z hmot Δmi který se otáčí po obvodu v rovině xy, každý má lineární rychlost vztahující se k jeho úhlové rychlosti, druhá stejná pro všechny částice:
protii = ωri
Kde ri je vzdálenost k ose otáčení O. Pak velikost momentu hybnosti je:
Li = Δmi. ri. (ωri) = ridvaω Δmi
Moment hybnosti systému bude dán součtem:
L = ω ∑ ridva Δmi
Rychle identifikujeme moment setrvačnosti, jak je definován v předchozí části, a proto velikost jeho momentu hybnosti je následující:
L = Iω
Jak jsme řekli, že částicový systém byl v rovině xy, ukázalo se, že moment hybnosti je směrován podél osy z, kolmo k uvedené rovině. Směr je dán směrem otáčení: moment hybnosti je kladný, pokud se otáčení provádí proti směru hodinových ručiček.
Rozšířené tělo lze rozdělit na plátky, z nichž každý má moment hybnosti daný L = Iω směřující podél osy z. Pokud se osa symetrie objektu shoduje s osou z, není problém, protože i pro body, které nejsou v rovině xy, se složky momentu hybnosti kolmé na tuto osu ruší.
Vektorově:
L = Jáω
Tato rovnice platí pro trojrozměrné objekty, které se otáčejí kolem osy symetrie.
Když síťová síla působí na částici nebo těleso, její hybnost se může změnit, a v důsledku toho se změní také její moment hybnosti. Abychom věděli, kdy se mění, použijeme derivaci, která nám dá rychlost změny v čase, pokud existuje:
Použití pravidla produktu pro derivát:
Termín proti x mproti je null, protože je výsledkem vektoru se sebou samým, a ve druhém členu najdeme čistou sílu F = mna, Tím pádem:
Vektorový produkt r X F není nic jiného než točivý moment nebo čistý točivý moment, někdy označovaný řeckým písmenem τ nebo jako M, vždy tučně, protože se jedná o vektorovou veličinu. Analogicky s lineární hybností se tedy moment hybnosti mění, pokud existuje čistý točivý moment nebo točivý moment:
dL/ dt = M
Z předchozích částí jsme viděli, že:
dL/ dt = M
To znamená, že moment hybnosti se mění, když existuje čistý točivý moment. Pokud není k dispozici čistý točivý moment, pak:
dL/ dt = 0 → L je to konstantní
Jinými slovy:
Počáteční moment hybnosti = Konečný moment hybnosti
Tento výsledek je stále platný i v případě, že tělo není tuhé, jak uvidíme v následujících příkladech.
Moment hybnosti je důležitá velikost, která se odhaluje v mnoha situacích, což ukazuje, jak je univerzální:
Kdykoli se rotující těleso smrští, jeho rychlost otáčení se zvýší, je to bruslařům dobře známo..
To je způsobeno skutečností, že když se paže a nohy smršťují, moment setrvačnosti I klesá, protože se zmenšuje vzdálenost mezi jejich částmi, ale protože se zachová moment hybnosti, aby se udržel konstantní součin Iω, musí se úhlová rychlost zvýšit.
To platí nejen při bruslení, ale také při sportu a činnostech, při nichž je nutné střídat, jako jsou potápěči a trapézoví umělci v cirkuse..
Kočkám se vždy podaří přistát na všech čtyřech, když spadnou. I když nemají počáteční hybnost, ujistěte se, že rychle otočíte nohama a ocasem, abyste změnili svou rotační setrvačnost a dokázali přistát..
Podobně, když manévrují, jejich moment hybnosti je nulový, protože jejich rotace není spojitá..
Frisbee musí být hozen tím, že se otočí, aby letěl, jinak padne. Moment hybnosti, který poskytuje odpalovací zařízení, dává puku dostatečnou stabilitu pro další pohyb ve vzduchu..
Míče v baseballu, fotbalu, basketbalu a jiných sportech mají momentální hybnost. Jelikož jsou sférické, mají moment setrvačnosti a během hry se otáčejí. Protože moment setrvačnosti koule je:
I = (2/5) MRdva
Kde M je hmotnost koule a R je její poloměr, moment setrvačnosti kolem určité (pevné) osy je:
L = (2/5) MRdvaω
Měsíc se vzdaluje od Země, protože rychlost rotace Země klesá v důsledku tření mezi velkými vodními hmotami a mořským dnem.
Systém Země-Měsíc zachovává svoji momentální hybnost, proto, pokud Země sníží svůj příspěvek, Měsíc zvýší svůj příspěvek a vzdaluje se od Země..
První postulát Bohrova atomového modelu uvádí, že elektron zaujímá pouze oběžné dráhy, kde moment hybnosti je celočíselný násobek h / 2π, kde h je Planckova konstanta.
Tenká ocelová tyč má hmotnost 500 g a délku 30 cm. Rotuje kolem osy procházející jejím středem rychlostí 300 otáček za minutu. Určete modul jeho momentu hybnosti.
Budeme potřebovat moment setrvačnosti tyče vztažené k ose, která prochází jejím středem. Z tabulek momentu setrvačnosti vyplývá, že:
I = (1/12) MLdva = (1/12) × 0,5 kg x (30 × 10-dva m)dva = 3,75 × 10-3 kg.mdva
Jelikož se jedná o prodloužené tělo, jehož úhlovou rychlost známe, použijeme:
L = Iω
Než transformujeme úhlovou rychlost nebo úhlovou frekvenci ω na radiány / s:
ω = (300 otáček za minutu) × (1 minuta / 60 sekund) x (2π radiány / otáčka) = 10 π rad / s
Střídání:
L = 3,75 x 10-3 kg⋅mdva × 10 π rad / s = 0,118 kg⋅mdva / s
Zatím žádné komentáře