V eliptickém pohybu popisuje mobil elipsu, stejně jako planety kolem Slunce a Měsíce a umělých satelitů kolem Země, abychom jmenovali několik známých příkladů..
Síla, která vede k tomuto pohybu, je gravitační síla, centrální síla. Tyto druhy sil jsou směrovány do (nebo z) pevného bodu O a jejich modul závisí na vzdálenosti k tomuto bodu. Pokud r je vzdálenost a nebor je jednotkový vektor v radiálním směru, centrální síla F je vektorová funkce formuláře:
F = F (r) nebor
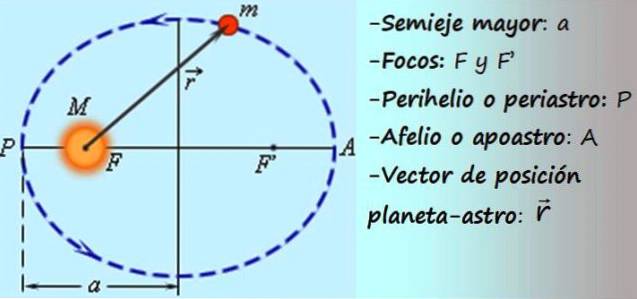
U některých matematik lze ukázat, že pohyb objektu působením gravitace sleduje jednu z těchto čtyř trajektorií: elipsa, obvod, hyperbola nebo parabola.
Některé z hlavních charakteristik eliptického pohybu pod centrální silou jsou:
-Moment hybnosti vzhledem k O je zachován, vyvolán L a to se vypočítá pomocí vektorového součinu mezi vektory polohy a rychlosti: L = r × mproti, kde m představuje hmotnost pohybujícího se objektu.
-Eliptická dráha leží v rovině určené vektory r Y proti.
-Ze zachování momentu hybnosti tzv zákon o oblastech, což stanoví, že mobilní zařízení cestuje stejnými oblastmi ve stejných časech.
-Mechanická energie je také zachována v eliptickém pohybu, pokud neexistují disipativní síly.
-Čas potřebný k tomu, aby mobil dal oběžnou dráhu, a její celková energie závisí pouze na délce „a“ poloviční hlavní osy elipsy..
Ačkoli se objekt pohybuje v kruhovém i eliptickém pohybu v uzavřené a opakující se dráze, tj. Periodické, existují zjevné rozdíly mezi jedním pohybem a druhým, například:
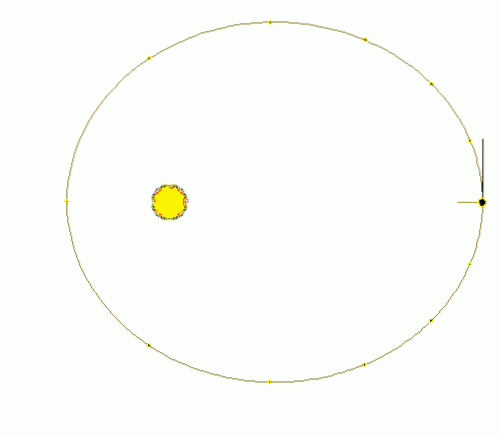
-V kruhovém pohybu popisuje mobil obvod, jehož poloměr (vzdálenost ke středu cesty) je konstantní, zatímco v eliptickém pohybu popisuje elipsu, ve které je vzdálenost ke středu cesty proměnlivá (viz obrázek 1).
-V případě rovnoměrného kruhového pohybu MCU mobilní zametá stejné úhly ve stejných časech, ale v planetárním eliptickém pohybu jsou zametány stejné oblasti ve stejných časech. Toto je zákon oblastí, známý také jako druhý Keplerův zákon planetárního pohybu..
V eliptickém pohybu odvozeném z gravitační přitažlivosti je doba T pohybu čas, který planetě nebo satelitu (m) trvá eliptický obrat kolem Slunce nebo Země (M). Při použití zachování energie vyplývá, že je úměrná krychli délky hlavní poloosy elipsy:
Kde G je univerzální gravitační konstanta: 6,67 × 10-jedenáct N ∙ mdva/ kgdva, M je hmotnost Slunce, Země nebo objektu způsobujícího interakci na m a „a“ je délka hlavní poloosy.
Celková energie pro planetu (m) - systém Slunce (M) je:
Velikost momentu hybnosti v bodě na eliptické oběžné dráze závisí také na délce hlavní poloosy a také na excentricitě „e“, bezrozměrném parametru, který udává, jak je elipsa zploštělá. Pokud e = 0, stane se z elipsy kruh.
Velikost rychlosti je dána následující rovnicí:
Kde r je vzdálenost mezi bodem na oběžné dráze (umístění planety) a ohniskem (Slunce).
První Keplerův zákon uvádí, že pohyb planet kolem Slunce sleduje eliptickou cestu, přičemž Slunce je v jednom z ohnisek. Některé komety, které pravidelně navštěvují Zemi, například Halleyova kometa, také sledují eliptický pohyb..
Kromě tohoto eliptického translačního pohybu a rotace kolem jejich osy mají planety své vlastní pohyby díky složitým gravitačním interakcím s ostatními planetami a nebeskými tělesy ve sluneční soustavě. Tímto způsobem jsou pohyby precese a nutice, které Země vlastní, a které jsou způsobeny společnou gravitační přitažlivostí Slunce a Měsíce..
V precesi popisuje zemská osa kužel, když se otáčí kolem osy kolmo k plánu nebo k ekliptice. A v nutaci, která je navrstvena na precesi, osa Země každých 18,6 let osciluje nahoru a dolů v eliptické smyčce. Celkem 1385 těchto smyček před 25 767 lety, což je období precese zemské osy.
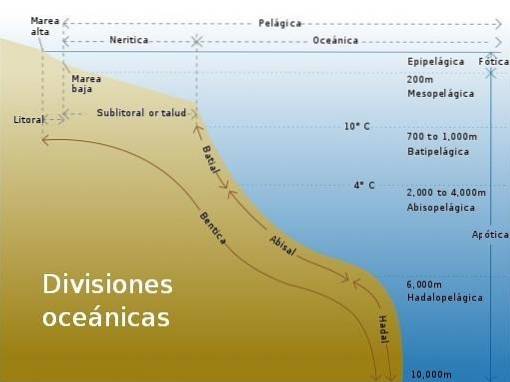
Ve vodách oceánu provádí částice eliptický pohyb, přičemž elipsa se s rostoucí hloubkou stále více zplošťuje. Na druhou stranu, když jsou vody hluboké, je pohyb částic kruhový.
Co se stane, je to, že když se vlna blíží k pobřeží, objeví se třecí síly díky jeho blízkosti ke dnu a toto tření má tendenci zpomalit pohyb ve spodní části trajektorie, zatímco hřeben pokračuje v pohybu..
Výsledkem je, že se obvod zploští a účinek se zvýrazní s rostoucí hloubkou..
Fyzické kyvadlo se skládá z tuhého tělesa, které může kmitat v rovině kolem osy kolmé na něj. Pokud se objekt může volně pohybovat, může popsat jakýkoli úhel kolem osy, který spojuje těžiště s bodem zavěšení, a také se kolem něj otáčet..
Díky rotaci Země je kyvadlo schopné popsat oběžné dráhy přibližně eliptického tvaru, které jsou známé jako eliptický režim oscilace, charakterizovaný jiným momentem hybnosti než 0.
Existují také režim roviny (moment hybnosti 0) a kónický režim (moment hybnosti jiný než 0), druhý s kruhovou dráhou v horizontální rovině.
Eliptické pohyby popsané dříve se vyskytují v přírodě, ale lze je také použít k výrobě užitečných pomůcek, jako jsou eliptická kola, což jsou velmi oblíbené stroje pro aerobik..
Jsou to stacionární kola, která se v zásadě skládají z řídítek a dvou pedálů, které se daná osoba aktivuje tím, že se tlačí svou váhou a popisuje elipsu nohama. Jedná se o přirozený pohyb s nízkým nárazem, který je přínosný, protože pohybuje mnoha svalovými skupinami po celém těle..
Zatím žádné komentáře