The přímočarý pohyb je ten, ve kterém se mobil pohybuje po přímce, a proto běží v jedné dimenzi, proto se také nazývá jednorozměrný pohyb. Tato přímka je trajektorie nebo cesta následovaná pohybujícím se objektem. Auta pohybující se podél aleje na obrázku 1 sledují tento typ pohybu.
Je to nejjednodušší model pohybu, jaký si dokážete představit. Denní pohyby lidí, zvířat a věcí obvykle kombinují pohyby v přímé linii s pohyby po křivkách, ale často jsou pozorovány pouze přímočaré pohyby.
Zde je několik dobrých příkladů:
- Při běhu po 200 metrů rovné trati.
- Řízení auta na rovné silnici.
- Volné upuštění objektu z určité výšky.
- Když je míč házen svisle nahoru.
Cíle popisu pohybu je nyní dosaženo specifikováním charakteristik, jako jsou:
- Pozice
- Přemístění
- Rychlost
- Akcelerace
- Počasí.
Aby mohl pozorovatel detekovat pohyb objektu, musí mít referenční bod (počátek O) a musí mít konkrétní směr pohybu, kterým může být osa X, osa Y nebo jakýkoli jiný.
Pokud jde o objekt, který se pohybuje, může mít nekonečné množství tvarů. V tomto ohledu neexistují žádná omezení, nicméně ve všem, co následuje, se bude předpokládat, že mobilní zařízení je částice; objekt tak malý, že jeho rozměry nejsou relevantní.
Je známo, že tomu tak není u makroskopických objektů; jedná se však o model s dobrými výsledky při popisu globálního pohybu objektu. Tímto způsobem může být částice auto, planeta, osoba nebo jakýkoli jiný objekt, který se pohybuje.
Začneme studovat přímočarou kinematiku s obecným přístupem k pohybu a poté budeme studovat konkrétní případy, jako jsou ty, které již byly pojmenovány..
Rejstřík článků
Následující popis je obecný a lze jej použít pro jakýkoli typ jednorozměrného pohybu. Nejprve je třeba zvolit referenční systém. Čára, podél které se bude pohybovat, bude osa X. Parametry pohybu:
Je to vektor, který jde od počátku do bodu, kde je objekt v daném okamžiku. Na obrázku 2 je vektor X1 označuje polohu mobilního telefonu, když je v souřadnici P1 a on včas t1. Jednotky vektoru polohy v mezinárodním systému jsou metrů.
Posunutí je vektor, který označuje změnu polohy. Na obrázku 3 se auto pohlo z polohy P1 do polohy Pdva, proto je jeho posun ΔX = Xdva - X1. Posunutí je odečtením dvou vektorů, je symbolizováno řeckým písmenem Δ („delta“) a jedná se zase o vektor. Jeho jednotky v mezinárodním systému jsou metrů.
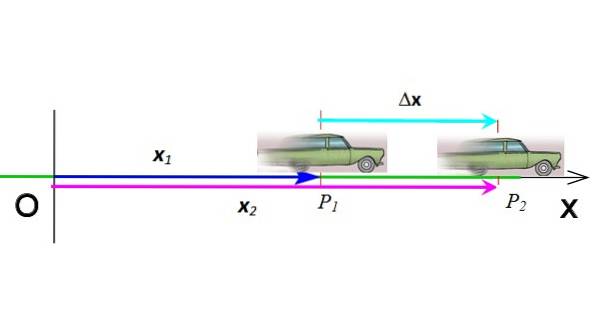
Vektory jsou v tištěném textu označeny tučně. Ale pokud máte stejnou dimenzi, můžete to udělat bez vektorové notace.
Vzdálenost d cestovaný pohybujícím se objektem je absolutní hodnota vektoru posunutí:
d = ΙΔXΙ = ΔX
Jako absolutní hodnota je ujetá vzdálenost vždy větší nebo rovna 0 a její jednotky jsou stejné jako jednotky polohy a posunutí. Zápis absolutní hodnoty lze provést pomocí pruhů modulo nebo jednoduše odstraněním tučného typu v tištěném textu.
Jak rychle se pozice mění? Existují pomalé mobily a rychlé mobily. Klíčem vždy byla rychlost. Pro analýzu tohoto faktoru se analyzuje poloha X funkce času t.
Průměrná rychlost protim (viz obrázek 4) je sklon sekanční linie (fuchsie) ke křivce X vs. t a poskytuje globální informace o pohybu mobilního telefonu v uvažovaném časovém intervalu.
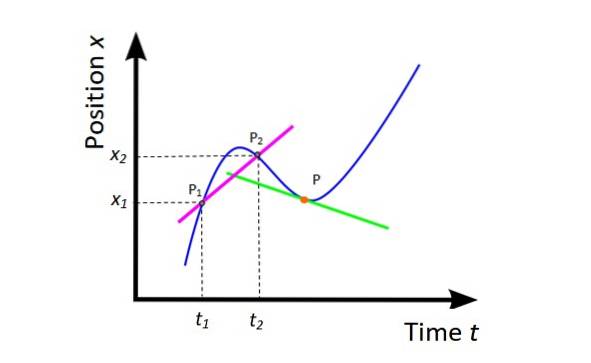
protim = (Xdva - X1) / (tdva -t1) = ΔX / Δt
Průměrná rychlost je vektor, jehož jednotkami v mezinárodním systému jsou metrů za sekundu (slečna).
Průměrná rychlost se počítá měřitelným časovým intervalem, ale nehlásí, co se v tomto intervalu stane. Chcete-li znát rychlost v každém okamžiku, musíte časový interval zmenšit na velmi malý, matematicky to odpovídá:
Δt → 0
Výše uvedená rovnice je uvedena pro průměrnou rychlost. Tímto způsobem se získá okamžitá rychlost nebo jednoduše rychlost:
Geometricky je derivací polohy vzhledem k času sklon linie tečny ke křivce X vs. t v daném bodě. Na obrázku 4 je bod oranžový a tečná čára zelená. Okamžitá rychlost v tomto bodě je sklon této přímky.
Rychlost je definována jako absolutní hodnota nebo modul rychlosti a je vždy kladná (značky, silnice a dálnice jsou vždy kladné, nikdy záporné). Výrazy „rychlost“ a „rychlost“ mohou být používány každý den zaměnitelně, ale ve fyzice je nutný rozdíl mezi vektorem a skalárem.
proti = ΙprotiΙ = proti
Rychlost se může v průběhu pohybu změnit a realita je taková, že se to očekává. Tuto změnu kvantifikuje velikost: zrychlení. Pokud si všimneme, že rychlost je změna polohy vzhledem k času, zrychlení je změna rychlosti vzhledem k času.
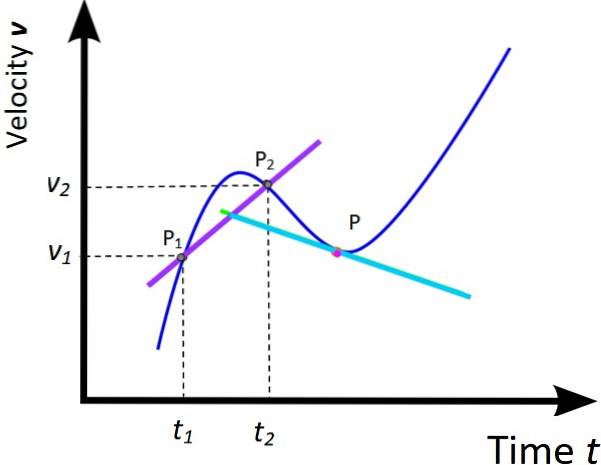
Ošetření dané grafu X vs. t dvou předchozích částí lze rozšířit na odpovídající graf proti vs. t. V důsledku toho jsou střední zrychlení a okamžité zrychlení definovány jako:
nam = (protidva - proti1) / (tdva -t1) = Δproti / Δt (Sklon fialové čáry)
V jednorozměrném pohybu mají vektory podle konvence pozitivní nebo negativní znaky podle toho, zda jdou tak či onak. Když má zrychlení stejný směr jako rychlost, zvyšuje jeho velikost, ale když má opačný směr a rychlost snižuje jeho velikost. Poté se říká, že pohyb je zpomalen.
Klasifikace přímočarých pohybů je obecně založena na:
- Zda je zrychlení konstantní nebo ne.
- Pohyb probíhá podél vodorovné nebo svislé čáry.
Když je zrychlení konstantní, průměrné zrychlení nam rovná se okamžité zrychlení na a existují dvě možnosti:
- Že zrychlení je rovno 0, v takovém případě je rychlost konstantní a existuje Uniform Rectilinear Motion nebo MRU.
- Konstantní zrychlení jiné než 0, při kterém se rychlost lineárně zvyšuje nebo snižuje s časem (Uniformly Varied Rectilinear Motion nebo MRUV):
Kde protiF Y tF jsou konečná rychlost a čas, a protinebo Y tnebo jsou to počáteční rychlost a čas. Ano tnebo = 0, Řešení pro konečnou rychlost máme již známou rovnici pro konečnou rychlost:
protiF = vnebo + na
Pro tento pohyb platí také následující rovnice:
- Pozice jako funkce času: x = xnebo + protinebo .t + ½ přidva
- Rychlost v závislosti na poloze: protiFdva = vnebodva + 2. ΔX (S Δx = x - xnebo)
Horizontální pohyby jsou ty, které probíhají podél vodorovné osy nebo osy x, zatímco svislé pohyby podél osy y. Vertikální pohyby působením gravitace jsou nejčastější a nejzajímavější.
V předchozích rovnicích bereme a = g = 9,8 m / sdva směrovaný svisle dolů, směr, který je téměř vždy zvolen se záporným znaménkem.
Takto, protiF = vnebo + na Transformuje se dovnitř protiF = vnebo - gt a pokud je počáteční rychlost 0, protože objekt byl volně vypuštěn, dále se zjednodušuje na protiF = - gt. Samozřejmě pokud se nebere v úvahu odpor vzduchu.
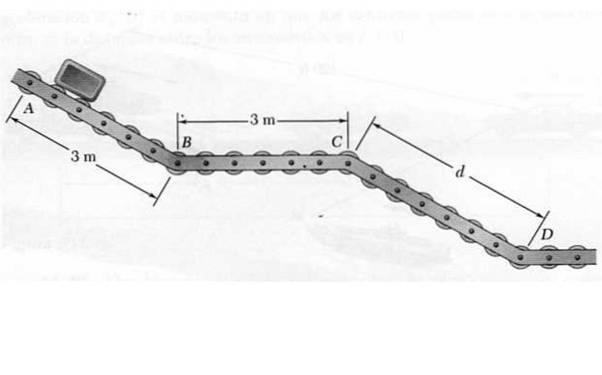
V bodě A se uvolní malé balení, které se bude pohybovat po dopravníku s posuvnými kolečky ABCD znázorněnými na obrázku. Při klesání ze svahů AB a CD má balík konstantní zrychlení 4,8 m / sdva, zatímco v horizontální části BC udržuje konstantní rychlost.
S vědomím, že rychlost, s níž paket dorazí na D, je 7,2 m / s, určete:
a) Vzdálenost mezi C a D.
b) Čas potřebný k tomu, aby balíček dosáhl konce.
Pohyb balíku se provádí ve třech zobrazených přímých úsecích a pro výpočet toho, co je požadováno, je požadována rychlost v bodech B, C a D. Pojďme analyzovat každý úsek zvlášť:
Protože čas není v této části k dispozici, bude použit protiFdva = vnebodva + 2. ΔX s vo = 0:
protiFdva = 2a.Δx → protiFdva= 2,8 m / sdva . 3 m = 28,8 mdva/ sdva → protiF = 5,37 m / s = vB
Čas potřebný k projetí paketu sekcí AB je:
tAB = (vF - protinebo) / a = 5,37 m / s / 4,8 m / sdva = 1,19 s
Rychlost v úseku BC je proto konstantní protiB = vC = 5,37 m / s. Čas potřebný na cestu paketem po této sekci je:
tpřed naším letopočtem = vzdálenost před naším letopočtem / vB = 3 m / 5,37 m / s = 0,56 s
Počáteční rychlost tohoto úseku je protiC = 5,37 m / s, konečná rychlost je protiD = 7,2 m / s, kolem protiDdva = vCdva + 2. a. d hodnota je vymazána d:
d = (protiDdva - protiCdva) /2.a = (7.2dva - 5.37dva)/dva X 4,8 m = 2,4 m
Čas se počítá jako:
tCD = (protiD - protiC) / a = (7,2 - 5,37) / 4,8 s = 0,38 s.
Odpovědi na položené otázky jsou:
a) d = 2,4 m
b) Cestovní doba je tAB + tpřed naším letopočtem + tCD = 1,19 s +0,56 s +0,38 s = 2,13 s.
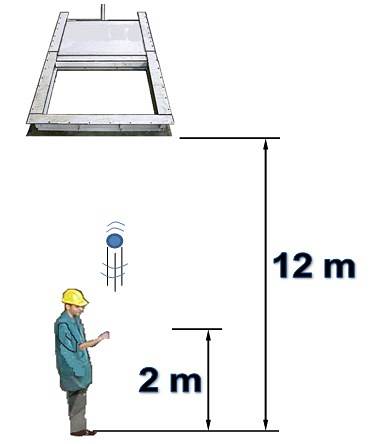
Osoba je pod vodorovnou bránou, která je zpočátku otevřená a vysoká 12 m. Osoba svisle hodí předmět směrem k bráně rychlostí 15 m / s.
Je známo, že brána se zavírá 1,5 sekundy poté, co osoba odhodila předmět z výšky 2 metrů. Odpor vzduchu nebude brán v úvahu. Odpovězte na následující otázky a zdůvodněte:
a) Může objekt projít bránou, než se zavře?
b) Narazí někdy objekt na zavřenou bránu? Pokud ano, kdy ano?
Mezi počáteční polohou míče a brankou je 10 metrů. Jedná se o svislý hod nahoru, ve kterém je tento směr považován za pozitivní.
Můžete zjistit rychlost potřebnou k dosažení této výšky, s tímto výsledkem se vypočítá čas, který by to trvalo, a porovná se s dobou zavírání brány, která je 1,5 sekundy:
protiF dva= vnebo dva- 2 g. Δa → protiF = (15dva - dva X 9.8 X10)1/2 m = 5,39 m / s
t = (vF - protinebo) / g = (5,39 - 15) / (-9,8) s = 0,98 s
Protože tato doba je kratší než 1,5 sekundy, dochází k závěru, že objekt může bránou projít alespoň jednou.
Již víme, že objekt dokáže projít bránou při stoupání, uvidíme, jestli mu dá šanci projít znovu při sestupu. Rychlost při dosažení výšky brány má stejnou velikost, jako když jde do kopce, ale v opačném směru. Proto pracujeme s rychlostí -5,39 m / s a čas potřebný k dosažení této situace je:
t = (vF - protinebo) / g = (-5,39 - 15) / (-9,8) s = 2,08 s
Jelikož brána zůstává otevřená pouze 1,5 s, je zřejmé, že před zavřením nemá čas znovu projít, protože ji najde zavřenou. Odpověď zní: objekt, pokud se srazí s uzavřeným poklopem po 2,08 sekundách po hodu, když již klesá.
Zatím žádné komentáře