The náhodný výběr je to způsob, jak vybrat statisticky reprezentativní vzorek z dané populace. Část zásady, že každý prvek ve vzorku by měl mít stejnou pravděpodobnost výběru.
Remíza je příkladem náhodného výběru, ve kterém je každému členu populace účastníků přiděleno číslo. K výběru čísel odpovídajících cenům tomboly (ukázka) se používá některá náhodná technika, například extrakce čísel, která byla zaznamenána na identických kartách, z poštovní schránky.
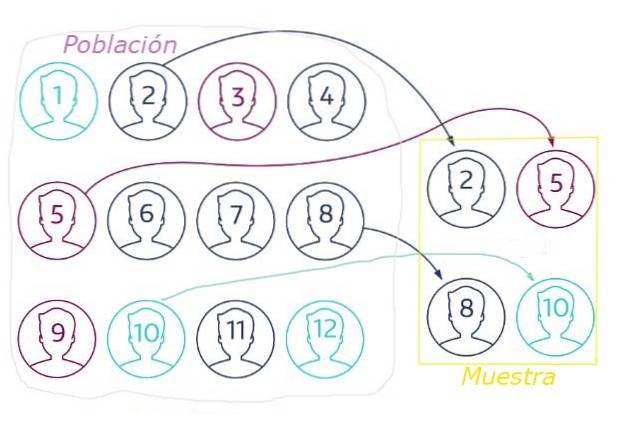
Při náhodném výběru je nezbytné správně zvolit velikost vzorku, protože nereprezentativní vzorek populace může vést ke špatným závěrům kvůli statistickým výkyvům..
Rejstřík článků
Existují vzorce pro určení správné velikosti vzorku. Nejdůležitějším faktorem, který je třeba vzít v úvahu, je, zda je známa velikost populace. Podívejme se na vzorce, abychom určili velikost vzorku:
Když velikost populace N není známa, je možné vybrat vzorek přiměřené velikosti n, aby bylo možné určit, zda je určitá hypotéza pravdivá nebo nepravdivá.
K tomu se používá následující vzorec:
n = (Zdva p q) / (E.dva)
Kde:
-p je pravděpodobnost, že hypotéza je pravdivá.
-q je pravděpodobnost, že tomu tak není, proto q = 1 - p.
-E je relativní hranice chyby, například chyba 5% má hranici E = 0,05.
-Z má co do činění s úrovní důvěry vyžadovanou studií.
Ve standardizovaném (nebo normalizovaném) normálním rozdělení má úroveň spolehlivosti 90% Z = 1,645, protože pravděpodobnost, že výsledek je mezi -1,645σ a + 1,645σ, je 90%, kde σ je směrodatná odchylka.
1. - 50% úroveň spolehlivosti odpovídá Z = 0,675.
2. - 68,3% úroveň spolehlivosti odpovídá Z = 1.
3. - 90% úroveň spolehlivosti odpovídá Z = 1645.
4. - 95% úroveň spolehlivosti odpovídá Z = 1,96
5. - 95,5% úroveň spolehlivosti odpovídá Z = 2.
6. - 99,7% úroveň spolehlivosti odpovídá Z = 3.
Příkladem, kde lze tento vzorec použít, by mohla být studie, která stanoví průměrnou hmotnost oblázků na pláži.
Je zřejmé, že není možné studovat a vážit všechny oblázky na pláži, proto je vhodné odebrat vzorek co nejnáhodněji as příslušným počtem prvků..
Když je znám počet N prvků, které tvoří určitou populaci (nebo vesmír), chcete-li vybrat statisticky významný vzorek velikosti n jednoduchým náhodným výběrem, je to vzorec:
n = (Zdvap q N) / (NEdva + Zdvap q)
Kde:
-Z je koeficient spojený s úrovní spolehlivosti.
-p je pravděpodobnost úspěchu hypotézy.
-q je pravděpodobnost selhání v hypotéze, p + q = 1.
-N je velikost celkové populace.
-E je relativní chyba výsledku studie.
Metodika extrakce vzorků hodně závisí na typu studie, kterou je třeba provést. Proto má náhodný výběr vzorků nekonečný počet aplikací:
Například v telefonních průzkumech jsou lidé, s nimiž je třeba konzultovat, vybíráni pomocí generátoru náhodných čísel použitelného pro studovaný region..
Pokud chcete použít dotazník na zaměstnance velké společnosti, můžete se uchýlit k výběru respondentů prostřednictvím jejich čísla zaměstnance nebo čísla občanského průkazu.
Toto číslo musí být také vybráno náhodně, například pomocí generátoru náhodných čísel.
V případě, že se studie týká dílů vyrobených strojem, musí být díly vybrány náhodně, ale ze šarží vyrobených v různých denních dobách nebo v různé dny nebo týdny..
Jednoduché náhodné vzorkování:
- Umožňuje snížit náklady na statistickou studii, protože pro získání statisticky spolehlivých výsledků není nutné studovat celkovou populaci s požadovanou úrovní spolehlivosti a mírou chyb požadovanou ve studii.
- Vyvarujte se zaujatosti: jelikož výběr prvků, které mají být studovány, je zcela náhodný, studie věrně odráží charakteristiky populace, ačkoli byla studována pouze její část.
- Metoda není adekvátní v případech, kdy chcete znát preference v různých skupinách nebo vrstvách populace.
V tomto případě je výhodnější předem určit skupiny nebo segmenty, na kterých má být studie provedena. Jakmile jsou vrstvy nebo skupiny definovány, pak je-li vhodné použít náhodný výběr pro každou z nich..
- Je velmi nepravděpodobné, že by byly získány informace o menšinových sektorech, z nichž je někdy nutné znát jejich charakteristiky.
Například pokud jde o kampaň na nákladném produktu, je třeba znát preference nejbohatších menšinových sektorů.
Chceme studovat preference populace pro určitý kolový nápoj, ale u této populace neexistuje žádná předchozí studie, jejíž velikost není známa..
Na druhé straně musí být vzorek reprezentativní s minimální úrovní spolehlivosti 90% a závěry musí obsahovat procentuální chybu 2%..
-Jak určit velikost vzorku n?
-Jaká by byla velikost vzorku, kdyby se míra chyby uvolnila na 5%??
Vzhledem k tomu, že velikost populace není známa, se k určení velikosti vzorku používá výše uvedený vzorec:
n = (Zdvap q) / (E.dva)
Předpokládáme, že existuje stejná pravděpodobnost preference (p) pro naši značku nealkoholických nápojů jako preference (q), pak p = q = 0,5.
Na druhou stranu, protože výsledek studie musí mít procentuální chybu menší než 2%, pak relativní chyba E bude 0,02.
Nakonec hodnota Z = 1 645 vytváří úroveň spolehlivosti 90%.
Shrneme-li, máme následující hodnoty:
Z = 1645
p = 0,5
q = 0,5
E = 0,02
S těmito údaji se vypočítá minimální velikost vzorku:
n = (1645dva 0,5 0,5) / (0,02dva) = 1691,3
To znamená, že studie s požadovanou mírou chyb a se zvolenou mírou spolehlivosti musí mít vzorek respondentů nejméně 1692 jedinců, vybraných náhodným výběrem..
Pokud přejdete z okraje chyby 2% na 5%, nová velikost vzorku je:
n = (1645dva 0,5 0,5) / (0,05dva) = 271
Což je výrazně nižší počet jednotlivců. Závěrem lze říci, že velikost vzorku je velmi citlivá na požadovanou míru chyby ve studii..
Zatím žádné komentáře