
Úhly v obvodových typech, vlastnosti, řešená cvičení
Volala obvodové úhly ty, ve kterých se některé jeho prvky v daném obvodu protínají nebo protínají. Mezi nimi jsou následující:
1. - The středový úhel, jehož vrchol je ve středu obvodu a jeho strany jsou k němu sešikmeny, jak vidíme na následujícím obrázku:

2. - The vepsaný úhel, jehož vrchol je na obvodu a jeho strany jsou sečny nebo tečny k obvodu.
3.- Vnější úhel, jehož vrchol je mimo obvod, ale jeho strany jsou sečny nebo tečny k obvodu.
4. - The vnitřní úhel, s vrcholem uvnitř obvodu a jeho stranami k němu sečtěnými.
Všechny tyto úhly mají určité vzájemné vztahy a to nás vede k důležitým vlastnostem mezi úhly patřícími k danému kruhu.
Rejstřík článků
- 1 Vlastnosti
- 1.1 - Středový úhel
- 1.2 - Vepsaný úhel
- 1.3 - Vnější úhel
- 1.4 - Vnitřní úhel
- 2 Vyřešená cvičení
- 2.1 - Cvičení 1
- 2.2 - Cvičení 2
- 3 Odkazy
Vlastnosti
- Středový úhel
Středový úhel je definován jako úhel, jehož vrchol je ve středu obvodu a jeho strany protínají obvod.
Míra v radiánech středního úhlu je kvocient mezi subtending obloukem, to znamená obloukem obvodu mezi stranami úhlu a poloměrem obvodu.
Pokud je obvod jednotný, to znamená poloměr 1, pak mírou středového úhlu je délka oblouku, která odpovídá počtu radiánů.
Pokud chcete měřit středový úhel ve stupních, vynásobte měřítko v radiánech koeficientem 180 ° / π.
Přístroje pro měření úhlu, jako je úhloměr a goniometr, vždy používají středový úhel a délku podřízeného oblouku.
Jsou kalibrovány v sexageimálních stupních, což znamená, že kdykoli se s nimi měří úhel, na pozadí se měří délka oblouku podřízená středním úhlem.
Vlastnictví
Míra středového úhlu v radiánech se rovná délce podřízeného nebo zachycovacího oblouku děleno délkou poloměru.
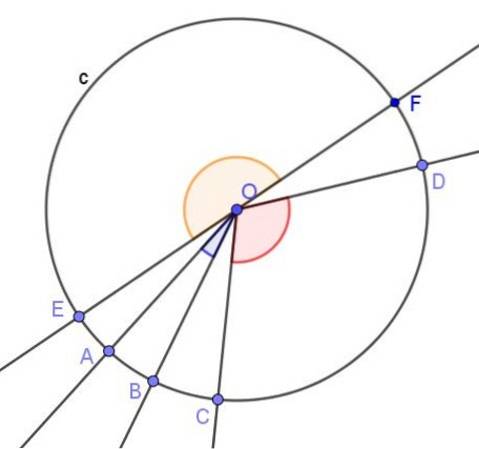
- Vepsaný úhel
Vepsaný úhel kruhu je úhel, který má svůj vrchol na obvodu a jeho paprsky jsou k němu sečny nebo tečny..
Jeho vlastnosti jsou:
Vlastnosti
-Vepsaný úhel je konvexní nebo rovinný.
-Když vepsaný úhel protíná stejný oblouk jako středový úhel, míra prvního úhlu bude poloviční oproti úhlu druhého..
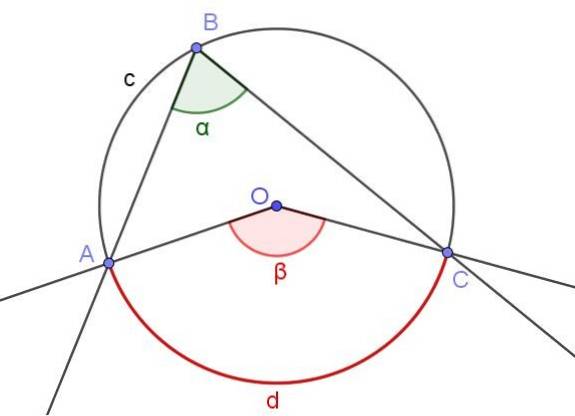
Obrázek 3 ukazuje dva úhly ∠ABC a ∠AOC, které protínají stejný oblouk obvodu A⌒C.
Pokud je míra vepsaného úhlu α, pak míra β středního úhlu je dvojnásobkem míry vepsaného úhlu (β = 2 α), protože obě mají stejný oblouk míry d.
- Vnější úhel
Je to úhel, jehož vrchol je mimo obvod a každá jeho strana prořezává obvod v jednom nebo více bodech.
Vlastnictví
-Jeho míra se rovná polovičnímu rozdílu (nebo rozdílu dělenému 2) středových úhlů, které zachycují stejné oblouky.
Aby bylo zajištěno, že měření bude kladné, musí být vždy poloviční rozdíl největšího středního úhlu minus míra nejmenšího středního úhlu, jak je znázorněno na následujícím obrázku.
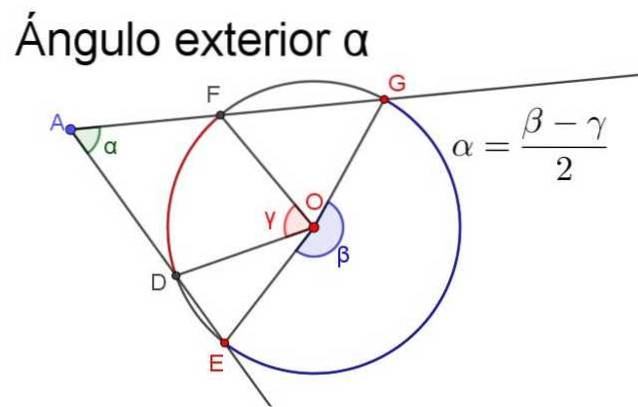
- Vnitřní úhel
Vnitřní úhel je ten, jehož vrchol je uvnitř obvodu a jeho strany protínají obvod.
Vlastnictví
Jeho míra se rovná polovičnímu součtu středového úhlu, který subtenduje stejný oblouk, plus středního úhlu, který subtends stejný oblouk jako jeho úhel rozšíření (to je vnitřní úhel tvořený paprsky komplementární k paprskům původního vnitřního úhlu ).
Následující obrázek ilustruje a objasňuje vlastnosti vnitřního úhlu.
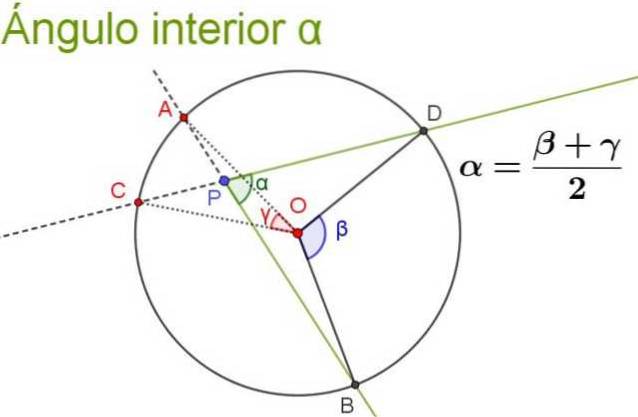
Vyřešená cvičení
- Cvičení 1
Předpokládejme vepsaný úhel, ve kterém jedna z jeho stran prochází středem kruhu, jak je znázorněno na obrázku 6. Poloměr kruhu je OA = 3 cm a oblouk d má délku π / 2 cm. Určete hodnotu úhlů α a β.
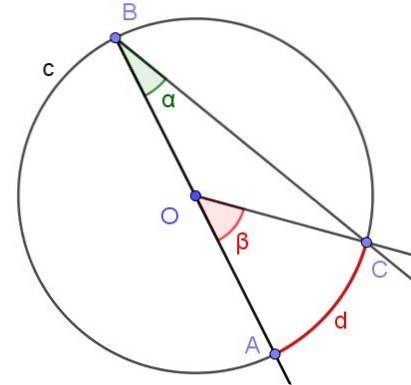
Řešení
V tomto případě se vytvoří rovnoramenný trojúhelník COB, protože [OC] = [OB]. V rovnoramenném trojúhelníku jsou úhly sousedící se základnou stejné, proto ∠BCO = ∠ABC = α. Na druhé straně ∠COB = 180º - β. Vzhledem k součtu vnitřních úhlů trojúhelníku COB máme:
α + α + (180 ° - β) = 180 °
Z čehož vyplývá, že 2 α = β, nebo co je ekvivalentní α = β / 2, se kterým je potvrzena vlastnost (3) předchozí části, že míra vepsaného úhlu je polovina středního úhlu, když oba úhly doplňte stejný akord [AC].
Nyní přistoupíme k určení číselných hodnot: úhel β je středový a jeho míra v radiánech je kvocient mezi obloukem d a poloměrem r = OA, takže jeho míra je:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30 °.
Na druhou stranu již bylo uvedeno, že α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Cvičení 2
Na obrázku 7 jsou úhly α1 a βdva mají stejnou míru. Dále úhel β1 měří 60 °. Určete úhly β a α.
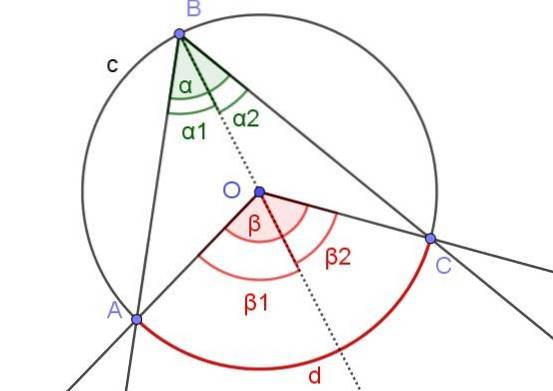
Řešení
V tomto případě máme vepsaný úhel ∠ABC, ve kterém je střed O obvodu v úhlu.
Kvůli vlastnosti (3) máme αdva = βdva / 2 a α1 = β1 /dva. Co:
α = α1 + αdva a β = β1 + βdva
Z toho tedy vyplývá, že:
α = α1 + αdva = β1 / 2 + βdva / 2 = (β1 + βdva) / 2 = β / 2.
To znamená podle vlastností:
α = β / 2
Protože nám bylo řečeno, že β1 = 60 ° pak:
α1 = β1 / 2 = 60 ° / 2 = 30 °.
Také nám říkají, že α1 = βdva z toho vyplývá, že:
βdva = 30 °.
Výsledek úhlu β:
β1 + βdva = 60 ° + 30 ° = 90 °.
A protože α = β / 2, pak:
α = 90 ° / 2 = 45 °.
Závěrem:
β = 90 ° a α = 45 °.
Reference
- Baldor, A. 1973. Geometrie a trigonometrie. Středoamerické kulturní nakladatelství.
- E. A. 2003. Prvky geometrie: cvičení a geometrie kompasu. University of Medellin.
- Geometrie 1. ESO. Úhly na obvodu. Obnoveno z: edu.xunta.es.
- Celá věda. Vyřešené problémy úhlů v obvodu. Obnoveno z: francesphysics.blogspot.com
- Wikipedia. Vepsaný úhel. Obnoveno z: es.wikipedia.com



Zatím žádné komentáře