
Nakloněná rovina k čemu to je, příklady, cvičení
The nakloněná rovina Jedná se o jednoduchý stroj, který se skládá z plochého povrchu, který svírá úhel vzhledem k horizontále. Jeho účelem je snížit úsilí potřebné k zvednutí předmětu do určité výšky.
Běžným použitím je zvedání těžkého břemene na stavební plošinu nebo vozidlo. Ze zkušeností víme, že tímto způsobem se úsilí sníží výměnou za to, že se trochu překoná vzdálenost..
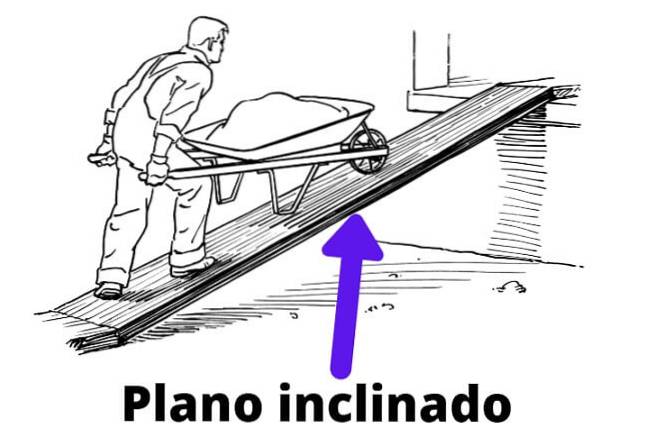
Takže namísto svislého zvedání objektu ve výšce h je provedeno cestování vzdáleností d po povrchu nakloněné roviny. Poté povrch přispívá k vyvážení části hmotnosti objektu, konkrétně jeho vertikální složky.
Použitá síla F Je zodpovědný za pohyb horizontální složky váhy, jejíž velikost je menší než samotná hmotnost. Proto velikost F je menší než velikost síly potřebné k přímému zvednutí těla.
Je požadováno snížení požadovaného úsilí mechanická výhoda, princip objevený velkým starověkým fyzikem Archimédem ze Syrakus (287-212 př. n. l.). Čím větší je mechanická výhoda, tím menší úsilí je třeba vynaložit na provedení úkolu.
Rejstřík článků
- 1 Příklady nakloněných rovin
- 1.1 Rampy
- 1.2 Klíny
- 1.3 Šrouby
- 2 Síly působící na objekt v nakloněné rovině
- 2.1 Normální a hmotnost
- 2.2 Normální, hmotnostní a kinetické tření
- 3 Cvičení vyřešeno
- 3.1 Řešení
- 4 Odkazy
Příklady nakloněných rovin
Jednoduché stroje, jako je nakloněná rovina, jsou známy již od pravěku. Raní lidé používali řezací nástroje z kamene k výrobě hrotů šípů k lovu a řezání dřeva k výrobě nádobí..
Mechanická výhoda M jednoduchého stroje je definována jako podíl mezi velikostí výstupní síly a velikostí vstupní síly. Jedná se tedy o bezrozměrné množství.
Velikost výstupní síly je obvykle větší než vstupní síla a M> 1. Existují však velmi choulostivé úkoly, které si zaslouží snížení výstupní síly, jako je tomu u svorek, pro které M < 1.
Jako příklady aplikace nakloněné roviny máme:
Rampy

Rampy jsou užitečné pro zvedání těžkých předmětů do určité výšky, vyžadující použití síly menší velikosti, než je hmotnost předmětu..
Mechanická výhoda M hladké rampy bez tření se vypočítá vytvořením kvocientu mezi jeho délkou, zvanou „d“ a její výškou, označenou jako „h“:
M = d / h
V praxi však dochází k tření mezi povrchy, proto je skutečná mechanická výhoda o něco menší než M (viz řešené cvičení 2).
Klíny
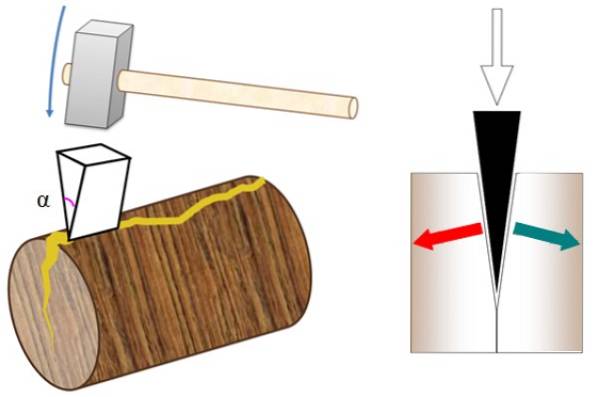
Skládají se z dvojité nakloněné roviny vyrobené z odolného materiálu se dvěma styčnými plochami, které zajišťují vysoké třecí síly v důsledku břitu, který se tvoří na hraně..
Řezná hrana je schopna překonat odpor materiálu a rozdělit jej na kousky pomocí kladiva k použití síly. Použití klínu je rozšířeno připojením rukojeti, jako je sekera.
Dobrým příkladem použití klínů jako řezných nástrojů jsou nože, sekery a dláta. Lidské řezáky jsou také tvarovány tak, aby rozřezávaly jídlo na menší, žvýkací kousky.
Čím delší je klín a čím menší je úhel na břitu, tím větší je mechanická výhoda nástroje, která je dána:
M = 1 / tg a
Kde α je úhel na břitu. Špičaté tvary, jako jsou klíny, nefungují jen k překonání odporu dřeva. Vozidla, jako jsou letadla a čluny, mají také klínové tvary, které překonávají odpor vzduchu a zvyšují rychlost..
Šrouby
V jiném každodenním zařízení, které se používá k upevnění dílů, je nakloněná rovina: šroub. Závit šroubu je nakloněná rovina navinutá kolem válcové osy šroubu.
Je použita vstupní síla Fi na šroub a při otáčení o jednu otáčku o velikosti 2πR, kde R je poloměr, šroub posune o vzdálenost p, tzv. Prošel. Tato vzdálenost je ta, která odděluje dva po sobě jdoucí závity šroubu.
Síly působící na objekt na nakloněné rovině
Normální a váha
Obrázek ukazuje diagram volného těla objektu v rovině nakloněné pod úhlem α. Za předpokladu, že nedojde k tření, jsou síly působící na objekt: normální N, působí kolmo a Ž hmotnost, která je svislá.
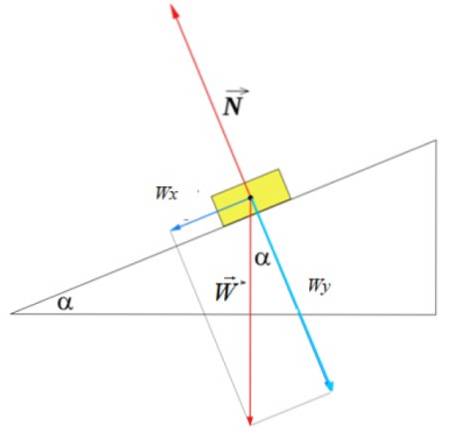
Složka závaží ve směru normály je WY, který kompenzuje tuto normálu, protože objekt se nepohybuje nad rovinou, ale rovnoběžně s ní. Síla F aplikovaný na objekt musí alespoň kompenzovat W složkuX tak, aby objekt stoupal po nakloněné rovině.
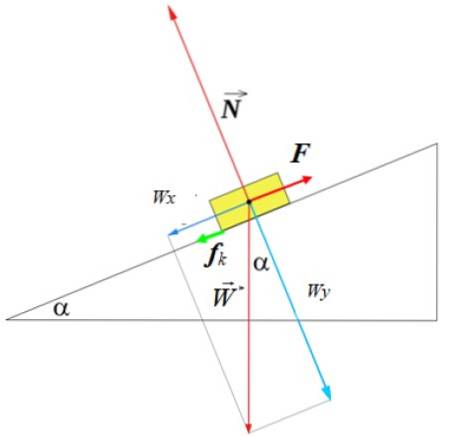
Normální, hmotnostní a kinetické tření
Pokud se uvažuje tření, je třeba vzít v úvahu, že je vždy proti pohybu nebo možnému pohybu. Když se objekt pohybuje na povrchu nakloněné roviny, působí kinetické tření, pokud jde objekt nahoru, kinetické tření Fk je směrován v opačném směru a síla F musí být také zodpovědná za jeho porážku.
Cvičení vyřešeno
Najděte úhel, který musí mít špička klínu, aby jeho mechanická výhoda byla 10.
Řešení
V předchozích částech bylo zjištěno, že mechanická výhoda M klínu byla dána:
M = 1 / tg a
Pokud M musí mít hodnotu 10:
1 / tg α = 10
tg α = 1/10 → α = 5,71 °
Reference
- E-škola dnes. Klín. Obnoveno z: eschooltoday.com.
- Resnick, R. 1999. Fyzika. Sv. 1. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. autor: C.V.
- Rex, A. 2011. Základy fyziky. Pearson.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.
- Tippens, P. 2011. Fyzika: koncepty a aplikace. 7. vydání. Mcgraw kopec.
- Wikipedia. Nakloněná rovina. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře