The mechanická síla je míra práce, která je matematicky vyjádřena množstvím práce za jednotku času. A protože práce se provádí na úkor absorbované energie, lze ji také uvést jako energii za jednotku času.
Povolání P k moci, Ž pracovat, A na energii a t Veškeré výše uvedené lze zároveň shrnout do snadno použitelných matematických výrazů:
Dobře:
Další pohonné jednotky používané v průmyslových odvětvích jsou hp (koňská síla nebo koňská síla) a CV (koňská síla). Původ těchto jednotek sahá také do doby Jamese Watta a průmyslové revoluce, kdy standardem měření byla rychlost, s jakou kůň pracoval..
Jak hp, tak CV jsou zhruba ekvivalentní ¾ kilo-W a jsou stále široce používány, zejména ve strojírenství, například při označování motorů.
V elektrické energii se také často používají násobky wattů, jako je výše zmíněný kilogram-W = 1 000 W. Je to proto, že joule je relativně malá jednotka energie. Britský systém používá libru stop za sekundu.
Rejstřík článků
Koncept síly je použitelný na všechny druhy energie, ať už mechanické, elektrické, chemické, větrné, zvukové nebo jakéhokoli druhu. Čas je v tomto odvětví velmi důležitý, protože procesy musí být provedeny co nejrychleji.
Jakýkoli motor provede potřebnou práci, pokud má dostatek času, ale důležité je udělat to v co nejkratším čase, aby se zvýšila účinnost..
Okamžitě je popsána velmi jednoduchá aplikace, která dobře objasňuje rozdíl mezi prací a mocí.
Předpokládejme, že těžký předmět je tažen lanem. K tomu je nutný nějaký externí agent, který provede nezbytnou práci. Řekněme, že tento agent přenáší 90 J energie do systému řetězců objektů, takže se uvede do pohybu po dobu 10 sekund.
V takovém případě je rychlost přenosu energie 90 J / 10 s nebo 9 J / s. Pak můžeme potvrdit, že tento agent, osoba nebo motor, má výstupní výkon 9 W..
Pokud je jiný externí agent schopen dosáhnout stejného přemístění, a to buď v kratším čase, nebo přenesením menšího množství energie, pak je schopen vyvinout větší sílu..
Další příklad: předpokládejme přenos energie 90 J, který dokáže uvést systém do pohybu po dobu 4 sekund. Výstupní výkon bude 22,5 W..
Síla úzce souvisí s výkonem. Energie dodávaná do stroje se nikdy úplně nezmění na užitečnou práci. Důležitá část je obvykle rozptýlena v teple, což závisí na mnoha faktorech, například na konstrukci stroje.
Proto je důležité znát výkonnost strojů, která je definována jako podíl mezi dodanou prací a dodanou energií:
η = práce dodaná strojem / dodaná energie
Kde je řecký dopis η označuje výnos, bezrozměrné množství, které je vždy menší než 1. Pokud je také vynásobeno 100, máme výnos v procentech.
- Lidé a zvířata rozvíjejí sílu během pohybu. Například lezení po schodech vyžaduje práci proti gravitaci. Ve srovnání se dvěma lidmi, kteří šplhají po žebříku, ten, kdo vyleze všechny kroky jako první, bude mít větší sílu než ostatní, ale oba odvedli stejnou práci.
- Domácí spotřebiče a stroje mají stanovený výstupní výkon. Žárovka vhodná pro osvětlení místnosti má výkon 100 W. To znamená, že žárovka přeměňuje elektrickou energii na světlo a teplo (většinu) rychlostí 100 J / s.
- Motor sekačky na trávu může spotřebovat přibližně 250 W a motor automobilu řádově 70 kW.
- Domácí vodní čerpadlo obvykle dodává 0,5 hp.
- Slunce generuje 3,6 x 10 26 Příkon W..
Okamžitá síla se získá nekonečným časem: P = dW / dt. Síla, která produkuje práci způsobující malé nekonečně malé posunutí dX to je F (oba jsou vektory), proto dW = F ● dX. Nahrazením všeho ve výrazu pro sílu zůstává:
Lidé jsou schopni alespoň na krátkou dobu generovat výkon kolem 1500 W nebo 2 koňské síly, například zvedání závaží.
V průměru je denní výkon (8 hodin) 0,1 hp na osobu. Většina z nich se převádí na teplo, přibližně stejné množství generované 75W žárovkou.
Sportovec v tréninku může generovat průměrně 0,5 hp, což odpovídá přibližně 350 J / s, transformací chemické energie (glukózy a tuku) na mechanickou energii.
Pokud jde o lidskou sílu, obecně se dává přednost měření v kaloriích za hodinu, spíše než ve wattech. Nezbytná rovnocennost je:
1 kilokalorie = 1 nutriční kalorie = 4186 J
Výkon 0,5 hp zní jako velmi malé množství a je vhodný pro mnoho aplikací.
V roce 1979 však bylo vytvořeno kolo poháněné člověkem, které mohlo létat. Paul MacCready navrhl Gossamer Albatross, který překročil kanál La Manche a generoval průměrný výkon 190 W (obrázek 1).
Důležitou aplikací je distribuce elektrické energie mezi uživateli. Společnosti, které dodávají elektřinu, účtují za spotřebovanou energii, nikoli za míru její spotřeby. Proto ti, kdo si pečlivě přečtou váš účet, najdou velmi specifickou jednotku: kilowatthodinu nebo kW-h..
Pokud je však v této jednotce zahrnut název Watt, vztahuje se to na energii, nikoli na výkon..
Kilowatthodina se používá k označení spotřeby elektrické energie, protože joule, jak již bylo zmíněno, je poměrně malá jednotka: 1 watthodina nebo W-h je práce odvedená za 1 hodinu při výkonu 1 watt.
Proto 1 kW-h je práce, která se provádí za hodinu a pracuje s výkonem 1 kW nebo 1 000 W. Pojďme dát čísla pro převod těchto množství na jouly:
1 š-v = 1 W x 3600 s = 3600 J
1 kW-h = 1 000 W x 3 600 s = 3,6 x 10 6 J
Odhaduje se, že domácnost může spotřebovat přibližně 200 kWh za měsíc.
Zemědělec pomocí traktoru vytáhne balík sena M = 150 kg na 15 ° nakloněnou rovinu a odnese jej do stodoly konstantní rychlostí 5,0 km / h. Koeficient kinetického tření mezi balíkem sena a žlabem je 0,45. Zjištění výkonu traktoru.
U tohoto problému je nutné nakreslit diagram volného těla balíku sena, který stoupá na svahu. Být F síla použitá traktorem ke zvednutí balíku, α = 15 ° je úhel sklonu.
Kromě toho je zapojena kinetická třecí síla Fdotek který je proti pohybu plus normální N a váha Ž (nezaměňujte hmotnost W s hmotností práce).
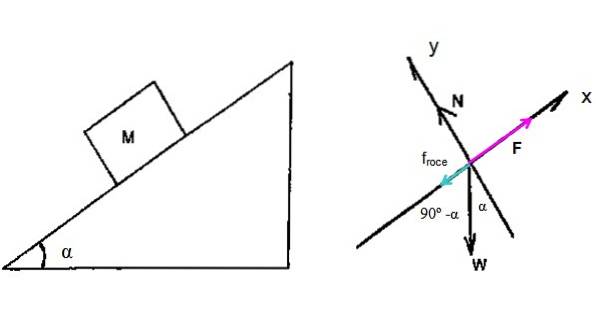
Newtonův druhý zákon nabízí následující rovnice:
∑ Fx = F-WX -Fdotek = 0 (protože balík stoupá konstantní rychlostí)
∑Fy = N - WY = 0 (nedochází k žádnému pohybu podél osy x)
Kinetická třecí síla se vypočítá z:
Fdotek = koeficient kinetického tření x velikost normálu
Fdotek = 0,45. Wy = 0,45 x 150 kg x 9,8 m / s2 x cos 15º = 639 N
F = ŽX + Fdotek = M.g. hřích α = 150 kg. 9,8 m / sdva . hřích 15º + 639 N = 1019,42 N
Rychlost a síla mají stejný směr a smysl, proto:
P = F ● proti = F. v
Je nutné transformovat jednotky rychlosti:
v = 5,0 km / h = 1,39 m / s
Dosazením hodnot nakonec dostaneme:
P = 1019,42 N x 1,39 m / s = 1417 W = 1,4 kW
Motor zobrazený na obrázku zvedne blok o hmotnosti 2 kg, počínaje od klidu, se zrychlením 2 m / sdva a za 2 sekundy.
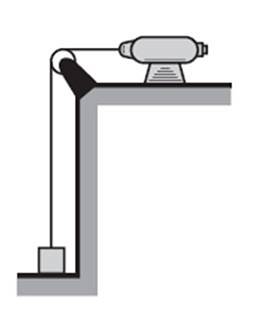
Vypočítat:
a) Výška dosažená blokem v té době.
b) Síla, kterou musí motor vyvinout, aby toho dosáhlo.
a) Jde o rovnoměrně proměnlivý přímočarý pohyb, proto budou použity odpovídající rovnice s počáteční rychlostí 0. Dosažená výška je dána vztahem:
y = ½ atdva = ½. 2 m / sdva . (2 s)dva = 4 m.
b) K nalezení výkonu vyvinutého motorem lze použít rovnici:
P = ΔW / Δt
A protože síla vyvíjená na blok je prostřednictvím napětí v řetězci, které je konstantní ve velikosti:
P = (ma) y / Δt = 2 kg x 2 m / sdva x 4 m / 2 s = 8 W.
Zatím žádné komentáře