
Princip propustnosti sil
Jaká je zásada přenositelnosti?
The zásada přenositelnosti se aplikuje na pevné objekty a uvádí, že síla aplikovaná na nějaký bod na těle je ekvivalentní jiné síle stejné velikosti a směru, pokud je tato síla aplikována ve stejné linii, která obsahuje původní sílu.
Jakákoli síla stejné velikosti a směru tedy způsobí stejný účinek translačního a rotačního pohybu na objekt, pokud je jeho aplikační bod umístěn na stejné linii, jak je znázorněno na následujícím obrázku.
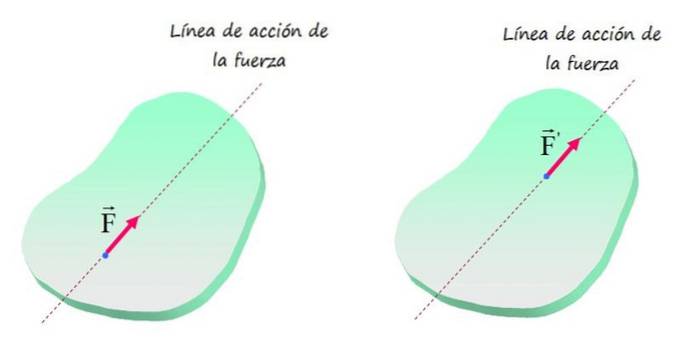
Zobrazené síly F Y F„Říká se, že jsou ekvivalentní síly a tečkovaná přímka, která je obsahuje, se nazývá linie působení.
Princip propustnosti je velmi užitečný, protože umožňuje, aby síly, které působí na objekt, pohodlně klouzaly, aby se usnadnila analýza..
Vysvětlení zásada přenositelnosti
Princip přenositelnosti je založen na skutečnosti, že dvě síly F1 Y Fdva jsou ekvivalentní, pokud mají stejnou velikost a stejný směr.
Kromě toho musí vyprodukovat stejný okamžik s ohledem na jakýkoli bod O, který je zaručen tím, že má stejnou linii působení a protože moment je součinem síly krát vzdálenost od O k uvedené linii..
Všimněte si, že princip platí pouze pro tuhé těleso, tj. Objekt, ve kterém se relativní vzdálenosti mezi jeho částmi nezmění, protože vnitřní síly, které jej drží pohromadě, jsou dostatečně silné. Objekt tedy nemění svůj tvar bez ohledu na to, zda na něj působí vnější síly..
Na druhou stranu, pokud objekt není tuhý, modifikace bodu působení sil by způsobila změny, pokud jde o napětí nebo tlak působící na tělo, což by vedlo ke změnám jeho tvaru..
Samozřejmě, za předpokladu, že tělo je tuhé, není nic jiného než idealizace, protože ve skutečnosti jsou všechny objekty deformovatelné ve větší či menší míře. V mnoha případech však jde o vynikající aproximaci, pokud je deformace dostatečně malá, aby ji bylo možné považovat za zanedbatelnou..
Omezení
Princip přenosnosti má, jak je uvedeno, omezení týkající se vnitřních účinků valivých nebo kluzných sil. Následující obrázek ukazuje objekt se silami F Y F'aplikován v různých bodech ve stejné linii akce.
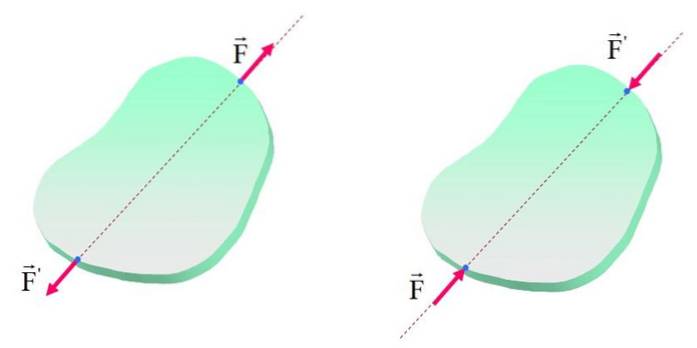
Všimněte si, že na obou obrázcích je těleso (tuhé nebo ne) v rovnováze, protože síly mají stejnou velikost a směr a opačné směry. Kromě toho jsou síly, jak již bylo řečeno, na stejném směru působení, ale na obrázku vlevo je účinek na tělo napjatý, zatímco na obrázku vpravo je účinek komprese..
Proto i když tělo zůstává v klidu, vnitřní účinky se liší a projeví se, pokud objekt není zcela tuhý. V případě levice mají síly tendenci tělo prodlužovat, zatímco v pravém mají tendenci jej zkracovat.
Příklady zásada přenositelnosti
Příklad 1
Předpokládejme, že máte těžký kufr na vodorovné podlaze. Efekt tlačení z levé strany je stejný jako tažení vodorovným lanem z pravé strany, přičemž obě síly působí podél zobrazené zelené vodorovné čáry. V tomto případě je pohyb kufru po zemi stejný.
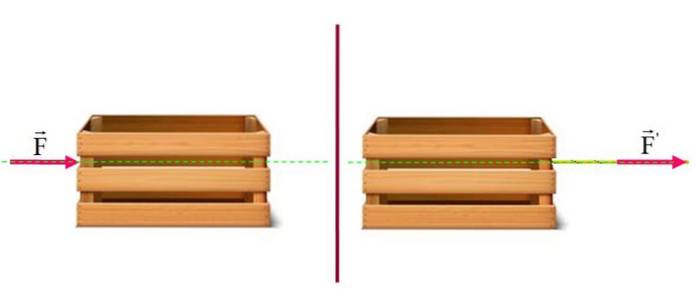
Příklad 2
Jako police je dlouhé prkno. Chcete-li jej nainstalovat, je ekvivalentní jej upevnit ze stropu pomocí lan na jeho koncích, než umístit vzpěry níže, také na stejných koncích.
V obou případech budou mít síly, které vyrovnávají prkno, stejnou velikost a směr, působící na stejné linie působení, ale jsou aplikovány v různých bodech..
Princip přenositelnosti a momentů
Předpokládejme, že máme sílu F aplikovanou v bodě A, okamžik, který vytváří tuto sílu kolem bodu O zobrazeného na obrázku, je:
MNEBO = rNA × F
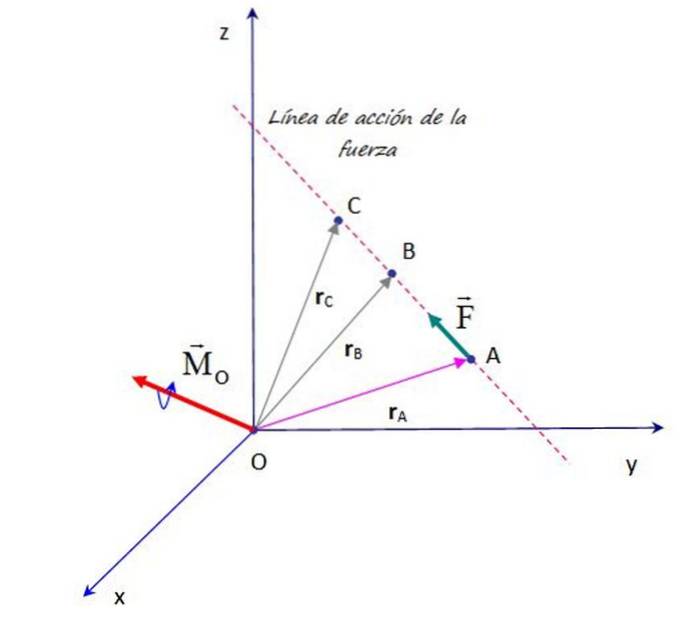
Zásada přenositelnosti to zajišťuje F, při působení na jakýkoli bod v jeho linii působení, například na body B, C a další, vzniká stejný okamžik ve vztahu k bodu O. Proto je třeba potvrdit, že:
MNEBO = rNA × F = rB × F = rC × F
Vyřešená cvičení
Cvičení 1
Homogenní koule má hmotnost M = 5 kg a je v klidu nesena na vodorovném povrchu bez tření.
-
- a) Nakreslete do diagramu sílu vyvíjenou povrchem na kouli.
- b) Vytvořte diagram volného tělesa koule
- c) Vypočítejte hodnotu normálové síly působící na povrch koule.
-
Řešení a a b
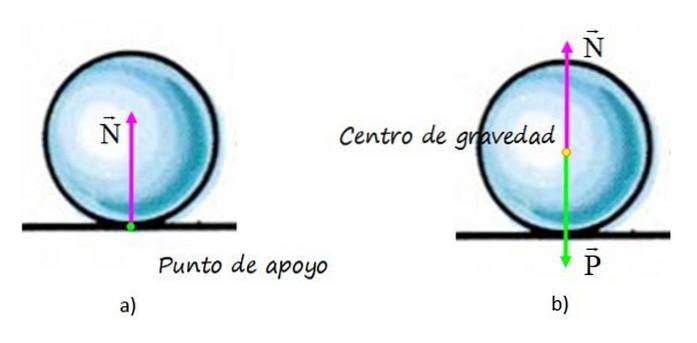
Graf a) ukazuje sílu vyvíjenou povrchem na kouli, která se nazývá normální N, protože je kolmá k povrchu. Bod aplikace síly se shoduje s bodem podpory koule na povrchu (bod v zelené barvě) a linie působení je vertikální, která prochází geometrickým středem koule..
V grafu b) je diagram volného tělesa koule, kde je kromě normálu zobrazena hmotnost, která je aplikována v těžišti, označená žlutě bodem.
Díky principu přenositelnosti je normální síla N lze ji posunout až do tohoto bodu, aniž by se změnily její účinky na kouli. Tyto efekty nejsou ničím jiným, než udržením koule spočívající na stole v rovnováze..
-
Řešení c
Vzhledem k tomu, že koule je v rovnováze, přičemž vertikální nahoru jako pozitivní a negativní vertikální dolů, vede Newtonův druhý zákon k:
N - P = 0
To znamená váhu a normální rovnováhu, proto jsou stejné velikosti:
N = P = Mg = 5 kg x 9,8 m / sdva = 49 N, směrovaný svisle nahoru.
Cvičení 2
Uveďte, zda je zásada převoditelnosti splněna v následujících případech:
-
První případ
Síla 20 N působící vodorovně na tuhé těleso je nahrazena další silou 15 N působící v jiném bodě těla, i když jsou obě působeny ve stejném směru.
-
- Řešení
V tomto případě nebude splněna zásada propustnosti, protože i když jsou obě síly aplikovány ve stejném směru, druhá síla nemá stejnou velikost jako první. Jedna z nezbytných podmínek zásady přenositelnosti tedy neexistuje..
-
Druhý případ
Síla 20 N působící vodorovně na tuhé těleso je nahrazena jinou silou 20 N působící v jiném bodě těla a svisle.
-
- Řešení
Při této příležitosti není splněn princip propustnosti, protože ačkoliv obě síly mají stejný modul, nejsou aplikovány ve stejném směru. Jedna z nezbytných podmínek zásady přenositelnosti opět neexistuje. Lze konstatovat, že tyto dvě síly jsou rovnocenné.
-
Třetí případ
Síla 10 N působící vodorovně na tuhé těleso se vymění za další také 10 N působící v jiném bodě tělesa, ale ve stejném směru a směru..
-
- Řešení
V tomto případě je splněn princip propustnosti, protože obě síly mají stejnou velikost a jsou aplikovány ve stejném směru a směru. Jsou splněny všechny nezbytné podmínky zásady přenositelnosti. Lze konstatovat, že tyto dvě síly jsou rovnocenné.
-
Čtvrtý případ
Síla klouže ve směru vaší akce rovně.
-
- Řešení
V tomto případě je splněna zásada přenositelnosti, protože při stejné síle se velikost použité síly nemění a klouže ve své linii působení. Opět jsou splněny všechny nezbytné podmínky zásady přenositelnosti.
Cvičení 3
Na tuhé těleso působí dvě vnější síly. Tyto dvě síly působí ve stejném směru a ve stejném směru. Pokud je modul prvního modulu 15 N a modulu druhého 25 N, jaké podmínky musí splňovat třetí vnější síla, aby nahradil výslednici předchozích dvou, aby splňoval princip propustnosti??
-
Řešení
Na jedné straně musí být hodnota výsledné síly 40 N, což je výsledek součtu modulu dvou sil.
Na druhou stranu musí výsledná síla působit v kterémkoli bodě přímky, která spojuje dva body působení obou sil..
Reference
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Beer, F. 2010. Vektorová mechanika pro inženýry. McGraw Hill. 5. Edice.
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Hibbeler, R. 2004. Engineering Mechanics: Statics. Hala Prentice.
- Meriam, J.L. 2012. Engineering Mechanics: Statics. 7. vydání. Wiley & Sons.



Zatím žádné komentáře