
Heptagonální hranolové charakteristiky, objem, plocha
A sedmihranný hranol Jedná se o geometrický útvar, který, jak naznačuje jeho název, zahrnuje dvě geometrické definice, které jsou: hranol a sedmiúhelník. „Hranol“ je geometrický útvar omezený dvěma základnami, které jsou rovné a rovnoběžné polygony a jejich boční plochy jsou rovnoběžníky..
„Sedmiúhelník“ je mnohoúhelník, který se skládá ze sedmi (7) stran. Protože sedmiúhelník je mnohoúhelník, může být pravidelný nebo nepravidelný.
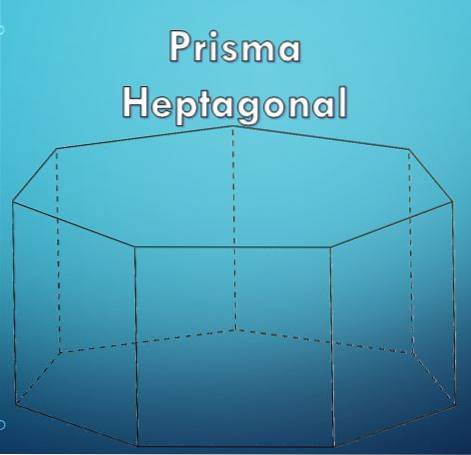
Polygon je považován za pravidelný, pokud všechny jeho strany mají stejnou délku a jeho vnitřní úhly jsou stejné, také se jim říká rovnostranné polygony; jinak se říká, že mnohoúhelník je nepravidelný.

Charakteristika sedmibokého hranolu
Níže jsou uvedeny určité vlastnosti, které má sedmiúhelníkový hranol, například: jeho konstrukce, vlastnosti jeho základen, plocha všech jeho ploch a jeho objem..
1- Konstrukce
K vybudování sedmibokého hranolu jsou nutné dva sedmiúhelníky, které budou jeho základnami a sedm rovnoběžníků, jeden pro každou stranu sedmiúhelníku..
Začnete nakreslením sedmiúhelníku, poté se nakreslí sedm svislých čar stejné délky, které vycházejí z každého z jeho vrcholů.
Nakonec je nakreslen další sedmiúhelník tak, aby se jeho vrcholy shodovaly s koncem čar nakreslených v předchozím kroku..
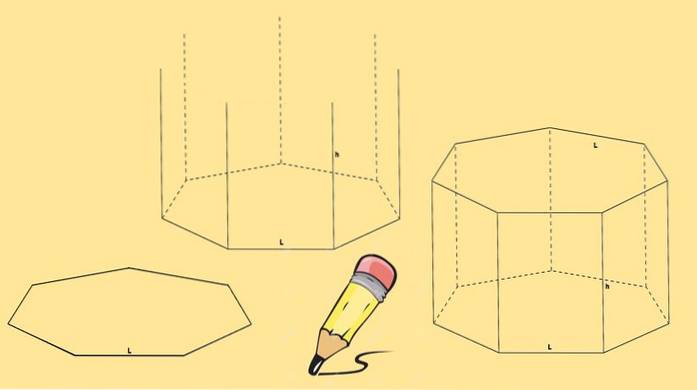
Heptagonální hranol nakreslený výše se nazývá pravý heptagonální hranol. Můžete ale mít i šikmý sedmiúhelníkový hranol, jako je ten na následujícím obrázku.

2 - Vlastnosti jeho základen
Protože jeho základny jsou sedmiúhelníky, uspokojují, že úhlopříčné číslo je D = nx (n-3) / 2, kde „n“ je počet stran mnohoúhelníku; v tomto případě máme D = 7 × 4/2 = 14.
Můžeme také vidět, že součet vnitřních úhlů libovolného sedmiúhelníku (pravidelného nebo nepravidelného) se rovná 900 °. To lze ověřit na následujícím obrázku.
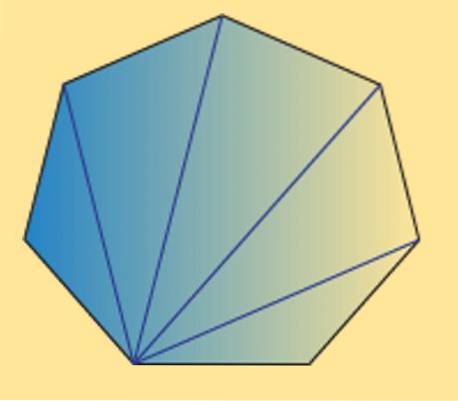
Jak je vidět, existuje 5 vnitřních trojúhelníků a pomocí toho, že součet vnitřních úhlů trojúhelníku se rovná 180 °, lze dosáhnout požadovaného výsledku.
3 - Prostor potřebný k vybudování Heptagonal Prism
Jelikož jeho základny jsou dva sedmiúhelníky a jeho strany jsou sedm rovnoběžníků, plocha potřebná k vytvoření sedmiúhelníkového hranolu se rovná 2xH + 7xP, kde „H“ je plocha každého sedmiúhelníku a „P“ je oblast každý rovnoběžník..
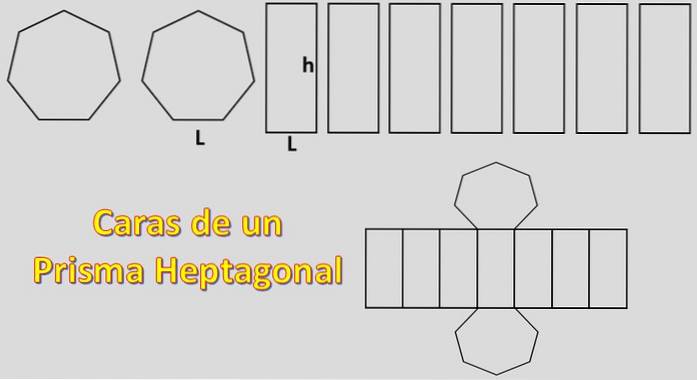
V tomto případě bude vypočítána plocha pravidelného sedmiúhelníku. K tomu je důležité znát definici apothemu.
Apothem je kolmá čára, která vede od středu pravidelného mnohoúhelníku do středu kterékoli z jeho stran.
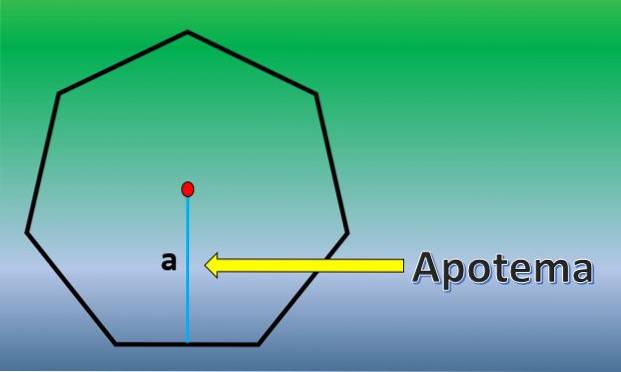
Jakmile je apothem znám, oblast sedmiúhelníku je H = 7xLxa / 2, kde „L“ je délka každé strany a „a“ je délka apothemu..
Plochu rovnoběžníku lze snadno vypočítat, je definována jako P = Lxh, kde „L“ má stejnou délku jako strana sedmiúhelníku a „h“ je výška hranolu..
Závěrem lze říci, že množství materiálu potřebného k vytvoření heptagonálního hranolu (s pravidelnými základnami) je 7xLxa + 7xLxh, tj. 7xL (a + h).
4 - Svazek
Jakmile je známa plocha základny a výška hranolu, je objem definován jako (plocha základny) x (výška).
V případě heptagonálního hranolu (s pravidelnou základnou) je jeho objem V = 7xLxaxh / 2; může být také zapsán jako V = Pxaxh / 2, kde "P" je obvod pravidelného sedmiúhelníku.
Reference
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: přístup k řešení problémů pro učitele základního vzdělávání. Redaktoři López Mateos.
- Fregoso, R. S., & Carrera, S. A. (2005). Matematika 3. Redakční program.
- Gallardo, G. a Pilar, P. M. (2005). Matematika 6. Redakční program.
- Gutiérrez, C. T. a Cisneros, M. P. (2005). Kurz matematiky 3. Redakční program.
- Kinsey, L. a Moore, T. E. (2006). Symetrie, tvar a prostor: Úvod do matematiky prostřednictvím geometrie (ilustrováno, dotisk ed.). Springer Science & Business Media.
- Mitchell, C. (1999). Oslnivé matematické linie (Ilustrované vydání.). Scholastic Inc..
- R., M. P. (2005). Nakreslím 6. místo. Redakční program.


Zatím žádné komentáře