
Charakteristiky lichoběžníkového hranolu, objem, plocha, aplikace
A lichoběžníkový hranol je hranol takový, že zapojené polygony jsou lichoběžníky. Definice hranolu je geometrické těleso tak, že je tvořeno dvěma stejnými a rovnoběžnými polygony a zbytek jejich ploch jsou rovnoběžníky.
Hranol může mít různé tvary, které závisí nejen na počtu stran mnohoúhelníku, ale na samotném mnohoúhelníku.
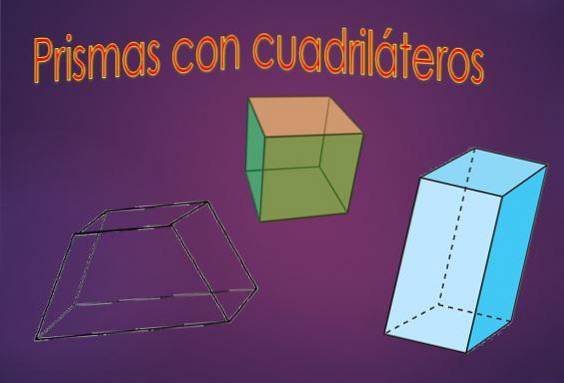
Pokud jsou polygony zapojené do hranolu čtverce, liší se to například od hranolu zahrnujícího kosočtverce, přestože oba polygony mají stejný počet stran. Proto záleží na tom, o jaký čtyřúhelník jde..
Vlastnosti lichoběžníkového hranolu
Chcete-li zobrazit vlastnosti lichoběžníkového hranolu, musíte nejprve vědět, jak je nakreslen, pak jaké vlastnosti základna splňuje, jaká je povrchová plocha a nakonec, jak se vypočítá jeho objem.
1- Kreslení lichoběžníkového hranolu
Chcete-li to nakreslit, je nutné nejprve definovat, co je to lichoběžník.
Lichoběžník je nepravidelný mnohoúhelník se čtyřmi stranami (čtyřúhelník), takže má pouze dvě rovnoběžné strany nazývané základny a vzdálenost mezi jejich základnami se nazývá výška..
Chcete-li nakreslit rovný lichoběžníkový hranol, začněte nakreslením lichoběžníku. Potom se z každého vrcholu promítne svislá čára délky „h“ a nakonec se nakreslí další lichoběžník tak, aby se jeho vrcholy shodovaly s konci dříve nakreslených čar..
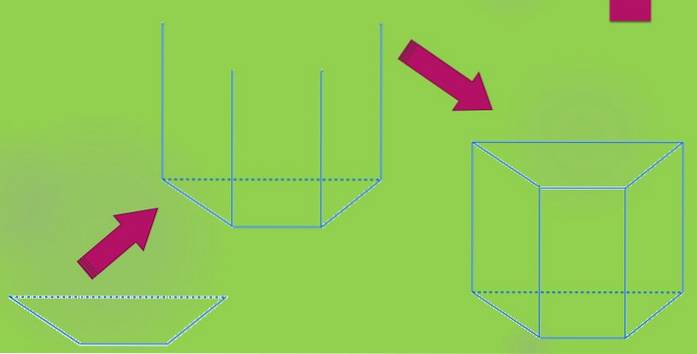
Můžete také mít šikmý lichoběžníkový hranol, jehož konstrukce je podobná té předchozí, stačí nakreslit čtyři čáry rovnoběžně k sobě.
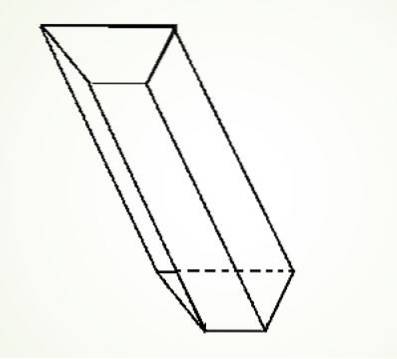
2 - Vlastnosti lichoběžníku
Jak již bylo řečeno, tvar hranolu závisí na mnohoúhelníku. V konkrétním případě lichoběžníku můžeme najít tři různé typy základen:
-Obdélník lichoběžník: je ten lichoběžník takový, že jedna z jeho stran je kolmá na rovnoběžné strany nebo že má jednoduše pravý úhel.

-Trapézové rovnoramenné: je lichoběžník takový, že jeho nerovnoběžné strany mají stejnou délku.
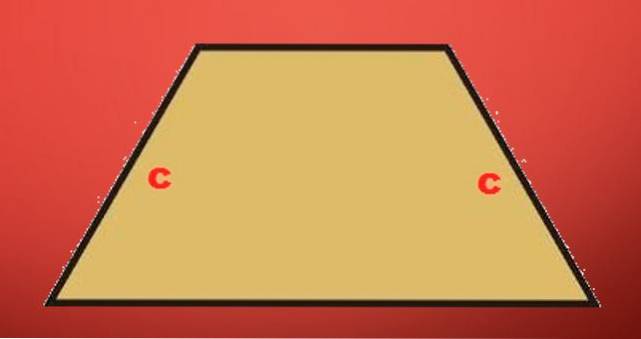
Scalene lichoběžník: je to ten lichoběžník, který není rovnoramenný nebo obdélníkový; jeho čtyři strany mají různé délky.

Jak je vidět, podle typu použitého lichoběžníku bude získán jiný hranol.
3- Povrchová plocha
Abychom mohli vypočítat povrch lichoběžníkového hranolu, musíme znát plochu lichoběžníku a plochu každého zapojeného rovnoběžníku..
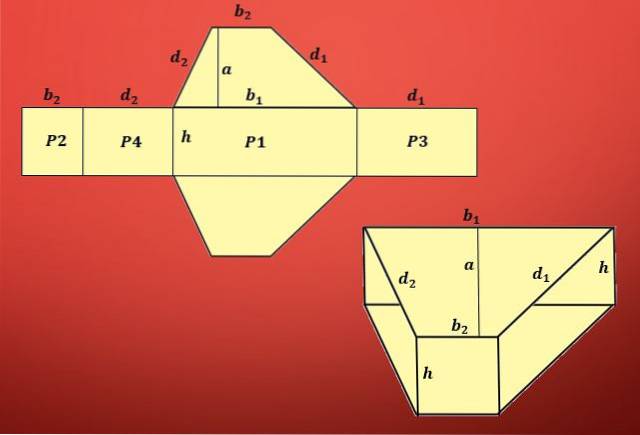
Jak je vidět na předchozím obrázku, oblast zahrnuje dva lichoběžníky a čtyři různé rovnoběžníky..
Plocha lichoběžníku je definována jako T = (b1 + b2) xa / 2 a oblasti rovnoběžníků jsou P1 = hxb1, P2 = hxb2, P3 = hxd1 a P4 = hxd2, kde „b1“ a „b2 „Jsou základny lichoběžníku,„ d1 “a„ d2 “nerovnoběžné strany,„ a “je výška lichoběžníku a„ h “výška hranolu.
Proto je povrch lichoběžníkového hranolu A = 2T + P1 + P2 + P3 + P4.
4 - Svazek
Protože objem hranolu je definován jako V = (plocha mnohoúhelníku) x (výška), lze vyvodit závěr, že objem lichoběžníkového hranolu je V = Txh.
5- Aplikace
Jedním z nejběžnějších předmětů, které mají tvar lichoběžníkového hranolu, je zlatý ingot nebo rampy používané v motocyklových závodech..

Reference
- Clemens, S. R., O'Daffer, P. G., & Cooney, T. J. (1998). Geometrie. Pearson Education.
- García, W. F. (s.f.). Spirála 9. Redakční Norma.
- Itzcovich, H. (2002). Studium postav a geometrických těles: aktivity pro první roky školní docházky. Knihy Noveduc.
- Landaverde, F. d. (1997). Geometrie (dotisk ed.). Redakční program.
- Landaverde, F. d. (1997). Geometrie (Dotisk ed.). Pokrok.
- Schmidt, R. (1993). Popisná geometrie se stereoskopickými obrazci. Reverte.
- Uribe, L., Garcia, G., Leguizamón, C., Samper, C., & Serrano, C. (s.f.). Alfa 8. Redakční Norma.



Zatím žádné komentáře