
Vzorec podmíněné pravděpodobnosti a rovnice, vlastnosti, příklady
The podmíněná pravděpodobnost Jedná se o možnost výskytu určité události, vzhledem k tomu, že další nastává jako podmínka. Tyto dodatečné informace mohou (ale nemusí) změnit vnímání toho, že se něco stane.
Můžeme si například položit otázku: „Jaká je pravděpodobnost, že dnes bude pršet, vzhledem k tomu, že nepršelo dva dny?“ Událostí, u které chceme vědět pravděpodobnost, je to, že dnes prší, a další informace, které by podmínku odpovědi byly, jsou: „nepršelo dva dny“.

Být pravděpodobnostní prostor složený z Ω (ukázkový prostor), ℬ (náhodné události) a P (pravděpodobnost každé události), plus události A a B, které patří do ℬ.
Podmíněná pravděpodobnost, že dojde k A, vzhledem k tomu, že došlo k B, která je označena jako P (A│B), je definována takto:
P (A│B) = P (A∩B) / P (B) = P (A a B) / P (B)
Kde: P (A) je pravděpodobnost výskytu A, P (B) je pravděpodobnost události B a liší se od 0, a P (A∩B) je pravděpodobnost průniku mezi A a B, tj. pravděpodobnost, že dojde k oběma událostem (společná pravděpodobnost).
Toto je výraz pro Bayesovu větu aplikovaný na dvě události, navržený v roce 1763 anglickým teologem a matematikem Thomasem Bayesem.
Rejstřík článků
- 1 Vlastnosti
- 1.1 Obecné pravidlo násobení
- 2 Příklady podmíněné pravděpodobnosti
- 2.1 - Příklad 1
- 2.2 - Příklad 2
- 3 Cvičení vyřešeno
- 4 Odkazy
Vlastnosti
-Každá podmíněná pravděpodobnost je mezi 0 a 1:
0 ≤ P (A│B) ≤ 1
-Pravděpodobnost, že dojde k události A, je vzhledem k této události zjevně 1:
P (A│A) = P (A∩A) / P (A) = P (A) / P (A) = 1
-Pokud jsou dvě události exkluzivní, to znamená události, které se nemohou stát současně, pak je podmíněná pravděpodobnost, že k jedné z nich dojde, 0, protože průnik je null:
P (A│B) = P (A∩B) / P (B) = 0 / P (B) = 0
-Pokud B je podmnožinou A, pak je podmíněná pravděpodobnost také 1:
P (B│A) = P (A∩B) / P (A) = 1
Důležité
P (A│B) se obecně nerovná P (B│A), proto musíme být při hledání podmíněné pravděpodobnosti opatrní, aby nedošlo k záměně událostí.
Obecné pravidlo násobení
Mnohokrát chcete najít společnou pravděpodobnost P (A∩B), nikoli podmíněnou pravděpodobnost. Potom prostřednictvím následující věty máme:
P (A∩B) = P (A a B) = P (A│B). P (B)
Věta může být rozšířena na tři události A, B a C:
P (A∩B∩C) = P (A a B a C) = P (A) P (B│A) P (C│A∩B)
A také pro různé akce, jako je A1, NAdva, NA3 a další, lze jej vyjádřit takto:
P (A.1∩ Adva ∩ A3… ∩ An) = P (A.)1). P (A.dva│A1). P (A.3│A1∩ Adva) ... P (A.n││A1∩ Adva∩… An-1)
Pokud se jedná o události, které se vyskytují postupně a v různých fázích, je vhodné uspořádat data do diagramu nebo tabulky. To usnadňuje vizualizaci možností k dosažení požadované pravděpodobnosti..
Příkladem toho jsou stromový diagram a pohotovostní tabulka. Z jednoho z nich můžete postavit druhý.
Příklady podmíněné pravděpodobnosti
Pojďme se podívat na některé situace, ve kterých se pravděpodobnost jedné události změní výskytem jiné:
- Příklad 1
V cukrárně se prodávají dva druhy koláčů: jahodový a čokoládový. Registrací preferencí 50 klientů obou pohlaví byly stanoveny následující hodnoty:
-27 žen, z nichž 11 dává přednost jahodovému a 16 čokoládovému.
-23 mužů: 15 si vybralo čokoládu a 8 jahod.
Pravděpodobnost, že si zákazník vybere čokoládový dort, lze určit pomocí Laplaceova pravidla, podle kterého je pravděpodobnost jakékoli události:
P = počet příznivých událostí / celkový počet událostí
V tomto případě z 50 zákazníků dává celkem 31 přednost čokoládě, takže pravděpodobnost by byla P = 31/50 = 0,62. To znamená, že 62% zákazníků dává přednost čokoládovému dortu.
Ale bylo by to jiné, kdyby klientem byla žena? Toto je případ podmíněné pravděpodobnosti.
Pohotovostní tabulka
Pomocí kontingenční tabulky, jako je tato, se snadno zobrazí součty:
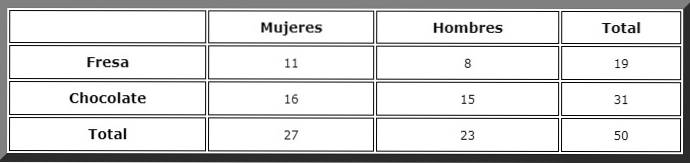
Poté jsou pozorovány příznivé případy a uplatní se Laplaceovo pravidlo, ale nejdříve definujeme události:
-B je událost „ženského klienta“.
-A je událost „upřednostňovat čokoládový dort“, být ženou.
Přejdeme ke sloupci označenému jako „ženy“ a tam vidíme, že celkem je 27.
Poté se hledá příznivý případ v řádku „čokoláda“. Těchto událostí je 16, proto je hledaná pravděpodobnost přímo:
P (A│B) = 16/27 = 0,5924
59,24% zákaznic preferuje čokoládový dort.
Tato hodnota se shoduje, když ji porovnáme s původně danou definicí podmíněné pravděpodobnosti:
P (A│B) = P (A∩B) / P (B)
Ujistíme se, že používáme Laplaceovo pravidlo a hodnoty tabulky:
P (B) = 27/50
P (A a B) = 16/50
Kde P (A a B) je pravděpodobnost, že zákazník preferuje čokoládu a je žena. Nyní jsou hodnoty nahrazeny:
P (A│B) = P (A a B) / P (B) = (16/50) / (27/50) = 16/27 = 0,5924.
A je dokázáno, že výsledek je stejný.
- Příklad 2
V tomto příkladu platí pravidlo násobení. Předpokládejme, že v obchodě jsou vystaveny kalhoty ve třech velikostech: malé, střední a velké..
U hodně s celkem 24 kalhotami, z nichž je 8 z každé velikosti a všechny jsou smíšené, jaká by byla pravděpodobnost vytažení dvou z nich a že oba byly malé?
Je jasné, že pravděpodobnost odstranění malých kalhotek na první pokus je 8/24 = 1/3. Nyní je druhá extrakce podmíněna první událostí, protože při odstraňování kalhot není jich už 24, ale 23. A pokud jsou odstraněny malé kalhotky, je jich 7 místo 8.
Událost A stahuje jedno malé kalhoty, když si na první pokus vytáhla další. A událost B je ta s malými kalhotami poprvé. Proto:
P (B) = 1/3; P (A│B) = 7/24
Nakonec pomocí pravidla násobení:
P (A∩B) = (7/24). (1/3) = 7/72 = 0,097
Cvičení vyřešeno
Ve studii dochvilnosti komerčních leteckých letů jsou k dispozici následující údaje:
-P (B) = 0,83, je pravděpodobnost, že letadlo vzlétne včas.
-P (A) = 0,81, je pravděpodobnost přistání včas.
-P (B∩A) = 0,78 je pravděpodobnost, že let přiletí včas a vzlétne včas.
Vyzývá se k výpočtu:
a) Jaká je pravděpodobnost, že letadlo přistane včas, protože vzlétlo včas?
b) Je předchozí pravděpodobnost stejná jako pravděpodobnost, kterou opustil včas, pokud se mu podařilo přistát včas??
c) A konečně: jaká je pravděpodobnost, že vzhledem k tomu dorazí včas ne vyšel včas?

Řešení
K zodpovězení otázky se používá definice podmíněné pravděpodobnosti:
P (A│B) = P (A∩B) / P (B) = P (A a B) / P (B) = 0,78 / 0,83 = 0,9398
Řešení b
V tomto případě jsou události v definici vyměněny:
P (B│A) = P (A∩B) / P (A) = P (A a B) / P (A) = 0,78 / 0,81 = 0,9630
Všimněte si, že tato pravděpodobnost se mírně liší od předchozí, jak jsme již dříve zdůraznili.
Řešení c
Pravděpodobnost, že neodejdete včas, je 1 - P (B) = 1 - 0,83 = 0,17, budeme to nazývat P (BC), protože se jedná o doplňkovou událost, která má vzlétnout včas. Hledaná podmíněná pravděpodobnost je:
P (A│BC) = P (A∩BC) / P (B.C) = P (A a BC) / P (B.C)
Na druhou stranu:
P (A∩BC) = P (přistání včas) - P (přistání včas a včasný vzlet) = 0,81-0,78 = 0,03
V tomto případě je hledaná podmíněná pravděpodobnost:
P (A│BC) = 0,03 / 0,17 = 0,1765
Reference
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Lipschutz, S. 1991. Schaum Series: Probability. Mcgraw kopec.
- Obregón, I. 1989. Teorie pravděpodobnosti. Redakční Limusa.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.
- Wikipedia. Podmíněná pravděpodobnost. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře