The vlastnosti rovnosti odkazují na vztah mezi dvěma matematickými objekty, ať už jde o čísla nebo proměnné. Je označen symbolem „=“, který se vždy nachází uprostřed těchto dvou objektů. Tento výraz se používá k určení, že dva matematické objekty představují stejný objekt; jinými slovy, že dva objekty jsou totéž.
Existují případy, kdy je triviální používat rovnost. Například je jasné, že 2 = 2. Pokud však jde o proměnné, již to není triviální a má konkrétní použití. Například pokud máme toto y = x a na druhé straně x = 7, můžeme dojít k závěru, že také y = 7.
Výše uvedený příklad je založen na jedné z vlastností rovnosti, jak brzy uvidíte. Tyto vlastnosti jsou nezbytné pro řešení rovnic (rovnosti zahrnujících proměnné), které tvoří velmi důležitou součást matematiky..
Rejstřík článků
Reflexivní vlastnost v případě rovnosti uvádí, že každé číslo se rovná sobě samému a je vyjádřeno jako b = b pro jakékoli reálné číslo b.
V konkrétním případě rovnosti se tato vlastnost zdá být zřejmá, ale v jiných typech vztahů mezi čísly tomu tak není. Jinými slovy, ne každý vztah se skutečnými čísly tuto vlastnost splňuje. Například takový případ vztahu „méně než“ (<); ningún número es menor que sí mismo.
Symetrická vlastnost pro rovnost říká, že pokud a = b, pak b = a. Nezáleží na pořadí použitém v proměnných, bude zachováno vztahem rovnosti.
Určitou analogii této vlastnosti s komutativní vlastností lze pozorovat v případě přidání. Například kvůli této vlastnosti je ekvivalentní zápisu y = 4 nebo 4 = y.
Transitivní vlastnost rovnosti uvádí, že pokud a = b a b = c, pak a = c. Například 2 + 7 = 9 a 9 = 6 + 3; podle tranzitivní vlastnosti tedy máme 2 + 7 = 6 + 3.
Jednoduchá aplikace je následující: Předpokládejme, že Julianovi je 14 let a Mario je stejného věku jako Rosa. Pokud je Rosa stejného věku jako Julian, jak starý je Mario?
Za tímto scénářem se tranzitivní vlastnost používá dvakrát. Matematicky se to interpretuje takto: ať „a“ je věk Maria, „b“ věk Rosy a „c“ věk Juliana. Je známo, že b = c a že c = 14.
Podle tranzitivní vlastnosti máme b = 14; to znamená, že Rosě je 14 let. Protože a = b a b = 14, opět používáme tranzitivní vlastnost a = 14; to znamená, že Marioův věk je také 14 let.
Jednotná vlastnost je, že pokud jsou obě strany rovnosti přidány nebo vynásobeny stejnou částkou, rovnost je zachována. Například pokud 2 = 2, pak 2 + 3 = 2 + 3, což je jasné, protože 5 = 5. Tato vlastnost je nejužitečnější při pokusu o vyřešení rovnice.
Předpokládejme například, že budete vyzváni k vyřešení rovnice x-2 = 1. Je vhodné si pamatovat, že řešení rovnice spočívá v explicitním určení příslušné proměnné (nebo proměnných) na základě konkrétního čísla nebo dříve určené proměnné..
Vrátíme-li se k rovnici x-2 = 1, musíte explicitně zjistit, kolik x stojí. Za tímto účelem musí být proměnná vymazána.
Bylo nesprávně učeno, že v tomto případě, protože číslo 2 je záporné, přechází na druhou stranu rovnosti s kladným znaménkem. Není však správné říkat to tak.
V zásadě to, co děláte, je použití jednotné vlastnosti, jak uvidíme níže. Myšlenka je vymazat „x“; to znamená, že to necháme na jedné straně rovnice. Podle dohody je obvykle ponechán na levé straně.
Za tímto účelem je číslo „vyloučeno“ -2. Způsob, jak to udělat, by byl přidáním 2, protože -2 + 2 = 0 a x + 0 = 0. Aby to bylo možné provést beze změny rovnosti, musí být na druhou stranu použita stejná operace.
To mu umožňuje realizovat uniformní vlastnost: protože x-2 = 1, je-li na obě strany rovnosti přidáno číslo 2, uniformní vlastnost říká, že se nezmění. Pak máme x-2 + 2 = 1 + 2, což je ekvivalentní tomu, že x = 3. Tím by byla rovnice vyřešena.
Podobně, pokud chcete vyřešit rovnici (1/5) y-1 = 9, můžete postupovat pomocí vlastnosti uniform takto:
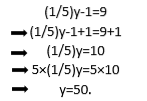
Obecněji lze učinit následující prohlášení:
- Pokud a-b = c-b, pak a = c.
- Pokud x-b = y, pak x = y + b.
- Pokud (1 / a) z = b, pak z = a ×
- Pokud (1 / c) a = (1 / c) b, pak a = b.
Vlastnost zrušení je konkrétní případ jednotné vlastnosti, zejména s ohledem na případ odčítání a dělení (který v zásadě také odpovídá sčítání a násobení). Tato vlastnost zachází s tímto případem samostatně.
Například pokud 7 + 2 = 9, pak 7 = 9-2. Nebo pokud 2y = 6, pak y = 3 (děleno dvěma na obou stranách).
Analogicky k předchozímu případu lze prostřednictvím vlastnosti zrušení vytvořit následující příkazy:
- Pokud a + b = c + b, pak a = c.
- Pokud x + b = y, pak x = y-b.
- Pokud az = b, pak z = b / a.
- Pokud ca = cb, pak a = b.
Pokud známe hodnotu matematického objektu, vlastnost substituce uvádí, že tuto hodnotu lze nahradit jakoukoli rovnicí nebo výrazem. Například pokud b = 5 a a = bx, dosazením hodnoty „b“ do druhé rovnosti máme, že a = 5x.
Další příklad je následující: pokud „m“ rozděluje „n“ a také „n“ rozděluje „m“, pak musí mít toto m = n.
Skutečnost, že „m“ rozdělí „n“ (nebo ekvivalentně, že „m“ je dělitelem „n“), znamená, že dělení m ÷ n je přesné; tj. vydělením „m“ číslem „n“ získáte celé číslo, nikoli desetinné číslo. To lze vyjádřit tím, že existuje celé číslo „k“ takové, že m = k × n.
Protože „n“ také rozděluje „m“, existuje celé číslo „p“ takové, že n = p × m. Kvůli vlastnosti substituce máme n = p × k × n, a aby se tak stalo, existují dvě možnosti: n = 0, v takovém případě bychom měli identitu 0 = 0; nebo p × k = 1, tedy identita n = n.
Předpokládejme, že „n“ není nenulové. Pak nutně p × k = 1; proto p = 1 ak = 1. Při opětovném použití substituční vlastnosti, když dosadíme k = 1 v rovnosti m = k × n (nebo ekvivalentně, p = 1 v n = p × m), nakonec získáme toto m = n, což jsme chtěli ukázat.
Stejně jako dříve bylo vidět, že pokud se operace, jako je sčítání, násobení, odčítání nebo dělení, provádí v obou podmínkách rovnosti, je zachována, stejně lze použít i jiné operace, které nemění rovnost..
Klíčem je vždy to provést na obou stranách rovnosti a předem se ujistit, že lze operaci provést. To je případ zmocnění; to znamená, že pokud jsou obě strany rovnice zvýšeny na stejnou moc, stále máme rovnost.
Například od 3 = 3, tak 3dva= 3dva (9 = 9). Obecně platí, že dané celé číslo „n“, pokud x = y, pak xn= an.
Toto je zvláštní případ zmocnění a je aplikován, když mocninou je necelé racionální číslo, například ½, které představuje druhou odmocninu. Tato vlastnost uvádí, že pokud se na obě strany rovnosti použije stejný kořen (kdykoli je to možné), rovnost se zachová.
Na rozdíl od předchozího případu je zde třeba dávat pozor na paritu použitého kořene, protože je dobře známo, že sudý kořen záporného čísla není dobře definován.
V případě, že je radikál sudý, není problém. Například pokud x3= -8, i když se jedná o rovnost, nemůžete například použít druhou odmocninu na obě strany. Pokud však můžete použít kořen krychle (což je ještě pohodlnější, pokud chcete explicitně znát hodnotu x), získáte x = -2.
Zatím žádné komentáře