
Jednotky magnetické neochoty, vzorce, výpočet, příklady
The magnetická neochota nebo magnetický odpor je opozice, kterou médium představuje pro průchod magnetického toku: čím vyšší je neochota, tím obtížnější je stanovení magnetického toku. V magnetickém obvodu má neochota stejnou roli jako elektrický odpor v elektrickém obvodu.
Cívka procházející elektrickým proudem je příkladem velmi jednoduchého magnetického obvodu. Díky proudu je generován magnetický tok, který závisí na geometrickém uspořádání cívky a také na intenzitě proudu, který protéká..

Rejstřík článků
- 1 Vzorce a jednotky
- 2 Jak se počítá magnetická neochota?
- 3 Rozdíl s elektrickým odporem
- 4 příklady
- 4.1 Solenoidy
- 4.2 Cívka navinutá na obdélníkové železné jádro
- 5 Cvičení vyřešena
- 5.1 - Cvičení 1
- 5.2 - Cvičení 2
- 6 Reference
Vzorce a jednotky
Označujeme magnetický tok jako Φm, ty máš:
Φm = N.i / (ℓC / μAC)
Kde:
-N je počet závitů cívky.
-Intenzita proudu je i.
-ℓC představuje délku obvodu.
-NAC je průřezová plocha.
-μ je propustnost média.
Faktorem ve jmenovateli, který kombinuje geometrii plus vliv média, je právě magnetická neochota obvodu, skalární veličina, která je označena písmenem ℜ, aby se odlišil od elektrického odporu. A) Ano:
ℜ = ℓC / μ.AC
V mezinárodním systému jednotek (SI) se ℜ měří jako inverze Henryho (vynásobená počtem závitů N). Henry je zase jednotka pro magnetickou indukčnost, ekvivalentní 1 tesle (T) x čtvereční metr / ampér. Proto:
1 HODINA-1 = 1 A / T.dva
Jako 1 t.mdva = 1 weber (Wb), neochota je také vyjádřena v A / Wb (ampér / weber nebo častěji ampér-turn / weber).
Jak se počítá magnetická neochota?
Protože magnetická reluktance má stejnou roli jako elektrický odpor v magnetickém obvodu, je možné u těchto obvodů rozšířit analogii o ekvivalent Ohmova zákona V = IR.
I když necirkuluje správně, magnetický tok Φm nahradí místo proudu místo napětí PROTI, definuje magnetické napětí nebo magnetomotorická síla, analogicky k elektromotorické síle nebo f.e.m v elektrických obvodech.
Magnetomotorická síla je odpovědná za udržování magnetického toku. Zkráceno f.m.m a je označen jako ℱ. S ním máme konečně rovnici, která spojuje tři veličiny:
ℱ = Φm . ℜ
A ve srovnání s rovnicí Φm = N.i / (ℓC / μAC), dochází k závěru, že:
ℱ = N.i
Tímto způsobem lze vypočítat neochotu se znalostí geometrie obvodu a propustnosti média, nebo také se znalostí magnetického toku a magnetického napětí, díky této poslední rovnici zvané Hopkinsonův zákon.
Rozdíl s elektrickým odporem
Rovnice pro magnetickou neochotu ℜ = ℓC / μAC je podobný R = L / σA pro elektrický odpor. V druhém případě σ představuje vodivost materiálu, L je délka drátu a A je jeho plocha průřezu.
Tyto tři veličiny: σ, L a A jsou konstantní. Nicméně propustnost média μ, obecně to není konstantní, takže ani magnetická neochota obvodu není na rozdíl od jeho elektrického přirovnání konstantní.
Pokud dojde ke změně média, například při přechodu ze vzduchu na železo nebo naopak, dojde ke změně propustnosti s následnou změnou neochoty. A také procházejí magnetické materiály hysterezní cykly.
To znamená, že aplikace vnějšího pole způsobí, že si materiál udrží část magnetismu, a to i po odstranění pole..
Z tohoto důvodu je při každém výpočtu magnetické neochoty nutné pečlivě určit, ve kterém bodě cyklu se materiál nachází, a znát tak jeho magnetizaci..
Příklady
Ačkoli neochota hodně závisí na geometrii obvodu, záleží také na propustnosti média. Čím vyšší je tato hodnota, tím menší je neochota; takový je případ feromagnetických materiálů. Na druhou stranu vzduch má nízkou propustnost, proto je jeho magnetická neochota vyšší..
Solenoidy
Solenoid je vinutí délky ℓ provedeno N závity, kterými prochází elektrický proud I. Závity jsou obecně navíjeny kruhově.
Uvnitř je generováno intenzivní a rovnoměrné magnetické pole, zatímco mimo pole je přibližně nula..
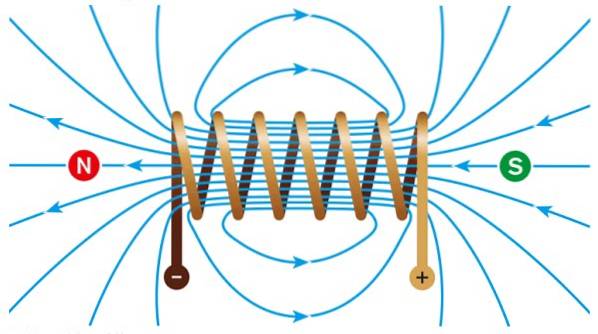
Pokud má vinutí kruhový tvar, existuje a torus. Uvnitř může být vzduch, ale pokud je umístěno železné jádro, magnetický tok je mnohem vyšší díky vysoké propustnosti tohoto minerálu.
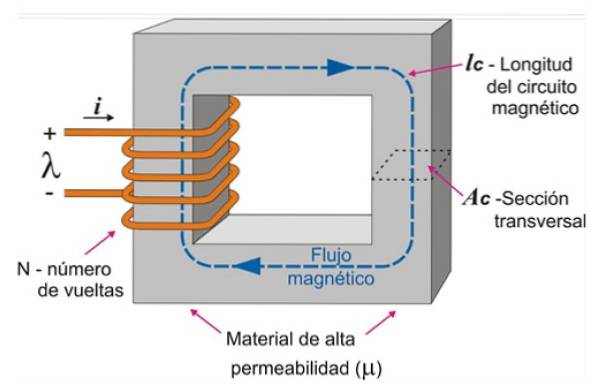
Cívka navinutá na obdélníkové železné jádro
Magnetický obvod lze vytvořit navinutím cívky na obdélníkové železné jádro. Tímto způsobem, když prochází proud drátem, je možné vytvořit intenzivní tok pole omezený uvnitř železného jádra, jak je znázorněno na obrázku 3.
Neochota závisí na délce obvodu a průřezu vyznačeném na obrázku. Zobrazený obvod je homogenní, protože jádro je vyrobeno z jediného materiálu a průřez zůstává jednotný..
Vyřešená cvičení
- Cvičení 1
Najděte magnetickou neochotu přímočarého solenoidu s 2000 otáčkami, protože víte, že když jím protéká proud 5 A, generuje se magnetický tok 8 mWb.
Řešení
Je použita rovnice ℱ = N.i. pro výpočet magnetického napětí, protože je k dispozici intenzita proudu a počet závitů v cívce. Jen se znásobuje:
ℱ = 2 000 x 5 A = 10 000 otáček zesilovače
Pak se použije ℱ = Φm . ℜ, dávat pozor na vyjádření magnetického toku ve weberu (předpona „m“ znamená „milli“, takže je vynásobena 10 -3:
Φm = 8 x 10 -3 Wb
Nyní je neochota odstraněna a hodnoty jsou nahrazeny:
ℜ = ℱ / Φm = 10 000 amp-turn / 8 x 10 -3 Wb = 1,25 x 106 zesilovač / turn / Wb
- Cvičení 2
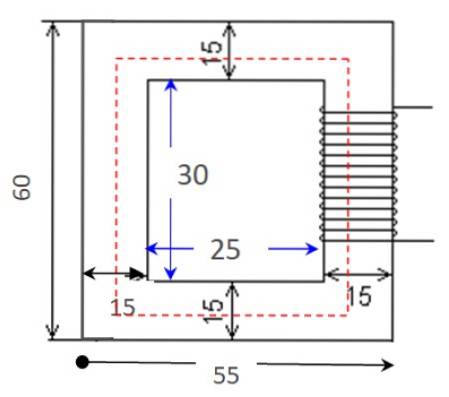
Vypočítejte magnetickou neochotu obvodu zobrazeného na obrázku s uvedenými rozměry, které jsou v centimetrech. Propustnost jádra je μ = 0,005655 Tm / A a plocha průřezu je konstantní, 25 cmdva.
Řešení
Použijeme vzorec:
ℜ = ℓC / μAC
Propustnost a průřezová plocha jsou k dispozici jako údaje ve výkazu. Zbývá najít délku obvodu, což je obvod červeného obdélníku na obrázku.
Z tohoto důvodu se délka vodorovné strany zprůměruje, přičemž se přidá větší délka a kratší délka: (55 +25 cm) / 2 = 40 cm. Poté postupujte stejně pro svislou stranu: (60 +30 cm) / 2 = 45 cm.
Nakonec se přidají průměrné délky čtyř stran:
ℓC = 2 x 40 cm + 2 x 45 cm = 170 cm
Odečtěte substituční hodnoty ve vzorci reluktance, ale ne dříve, než vyjádříte délku a plochu průřezu - uvedenou v příkazu - v jednotkách SI:
ℜ = 170 x 10 -dvam / (0,005655 Tm / A x 0,0025 mdva) = 120,248 zesilovač-otočka / Wb
Reference
- Alemán, M. Feromagnetické jádro. Obnoveno z: youtube.com.
- Magnetický obvod a neochota. Obnoveno z: mse.ndhu.edu.tw.
- Spinadel, E. 1982. Elektrické a magnetické obvody. Nová knihovna.
- Wikipedia. Magnetomotorická síla. Obnoveno z: es.wikipedia.org.
- Wikipedia. Magnetická neochota. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře