
Vysvětlení podmínek druhé rovnováhy, příklady, cvičení
The druhá rovnovážná podmínka stanoví, že součet momentů nebo momentů produkovaných všemi silami působícími na těleso, bez ohledu na to, v jakém bodě jsou vypočítány, musí být zrušen, aby uvedené těleso bylo ve statické nebo dynamické rovnováze.
Řeckým písmenem označíme točivý moment nebo moment síly τ, matematicky je to vyjádřeno takto:
∑ τ = 0

Tučné písmeno označuje vektorovou povahu okamžiku, který musí být zrušen s ohledem na jakýkoli bod vybraný jako střed otáčení. Tímto způsobem zrušení čistého točivého momentu zajistí, že se objekt nezačne otáčet nebo převrhávat..
Pokud se však objekt již dříve otáčel a čistý točivý moment náhle zmizel, bude rotace pokračovat, ale s konstantní úhlovou rychlostí.
Druhá podmínka rovnováhy se používá ve spojení s první podmínkou, která říká, že součet sil na tělese musí být nulový, aby se nepřekládal, nebo že pokud ano, je to s rovnoměrným přímočarým pohybem:
∑ F = 0
Obě podmínky platí pro rozšířená těla, jejichž rozměry jsou měřitelné. Když se předpokládá, že objekt je částice, nemá smysl mluvit o rotacích a první podmínka je dostatečná k zajištění rovnováhy.
Příklady
Druhá podmínka rovnováhy se projevuje v nesčetných situacích:
Jak stoupáte po žebříku
Při podepření žebříku na podlaze a na stěně potřebujeme dostatečné tření, zejména na podlaze, abychom zajistili, že žebřík neklouže. Pokud se pokusíme vylézt na žebřík podepřený na mastné, mokré nebo kluzké podlaze, není těžké předvídat, že spadneme.
Abyste mohli žebřík s jistotou používat, je nutné, aby byl při lezení a na požadované příčce ve statické rovnováze.
Stěhování skříně
Pokud chcete přemístit vysoký kus nábytku, jako je skříň, nebo jakýkoli kus, jehož výška je větší než jeho šířka, je vhodné tlačit na nízký bod, aby nedošlo k převrácení, tímto způsobem je pravděpodobnější, že nábytek se místo otáčení posouvá a lehne si.
Za takových okolností nemusí být nábytek nutně v rovnováze, protože by se mohl rychle pohybovat, ale alespoň by se nepřevrátil.
Balkony
Balkony, které vyčnívají z budov, by měly být postaveny tak, aby se zajistilo, že i když je nahoře mnoho lidí, nepřeklopí se a nespadne.
Dielektrika ve vnějších elektrických polích
Umístěním dielektrického materiálu do vnějšího elektrického pole se molekuly pohybují a otáčejí, dokud nepřijmou rovnovážnou polohu, čímž vytvoří elektrické pole uvnitř materiálu..
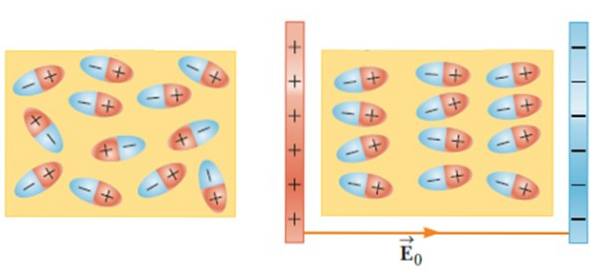
Tento efekt zvyšuje kapacitu kondenzátoru, když je mezi jeho rámy vložen materiál, jako je sklo, guma, papír nebo olej..
Značky a lampy
Je běžné, že mnoho místních obyvatel visí oznámení na zdi budovy, aby je viděli kolemjdoucí.
Plakát je držen barem a kabelem, oba jsou připevněny ke zdi pomocí držáků. Různé síly, které působí, musí zajistit, aby plakát neklesl, pro který vstupují do hry dvě rovnovážné podmínky.
Tímto způsobem lze do parku umístit také reflektor, jako na následujícím obrázku:
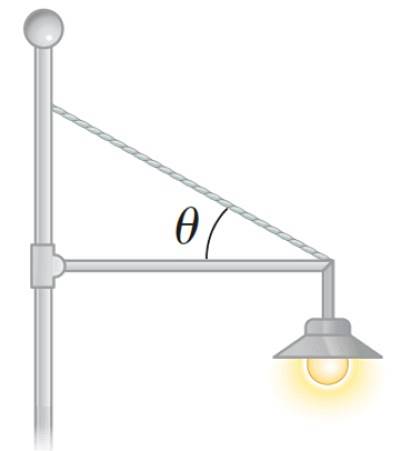
Jak vypočítat čistý točivý moment nebo čistý moment síly?
Točivý moment nebo moment síly, označený τ nebo M v některých textech se vždy počítá s ohledem na nějaký bod, kde prochází osa otáčení.
Je definován jako vektorový produkt mezi pozičním vektorem r, která je směrována z uvedené osy do bodu aplikace síly a síly F:
τ = r × F
Jako vektor je nutné vyjádřit točivý moment udáním jeho velikosti, směru a smyslu. Velikost je dána vztahem:
τ = rF.sen θ
Pravidlo pravé ruky pro vektorový produkt
Když je problém v rovině, směr točivého momentu je kolmý na papír nebo obrazovku a směr je určen pravidlem, ve kterém ukazováček směřuje k r, prostřední prst směrem k F a palec ukazuje dovnitř nebo ven z papíru.
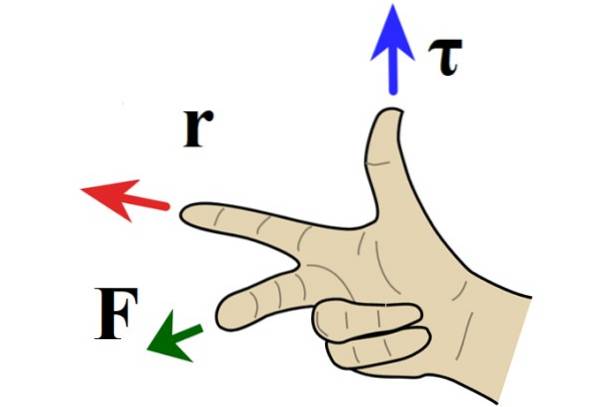
Když točivý moment ukazuje ven z papíru, rotace je proti směru hodinových ručiček a je podle konvence přiřazena kladná značka. Pokud je místo toho točivý moment nasměrován dovnitř lopatky, rotace je ve směru hodinových ručiček a záporná..
Pro zjištění čistého točivého momentu je pro výpočet zvolen vhodný bod, kterým může být ten, ve kterém působí největší množství sil. V tomto případě je moment těchto sil nulový, protože má vektor polohy r o velikosti 0.
Můžete si vybrat libovolný bod, který nabízí dostatek informací k vyřešení neznámého, který požaduje vyřešení problému. Podívejme se na to podrobněji níže.
Cvičení vyřešeno
Reflektor na následujícím obrázku má hmotnost 20 kg a je nesen tenkou vodorovnou tyčí zanedbatelné hmotnosti a délky L, která je zavěšena na sloupu. Kabel, také lehký, který pomáhá podepřít reflektor, svírá s tyčí úhel θ = 30 °. Vypočítat:
a) Napětí kabelu
b) Velikost síly F, kterou sloupek působí na tyč přes závěs.
Řešení
Použijeme první rovnovážnou podmínku ∑ F = 0 na síly zobrazené na obrázku:
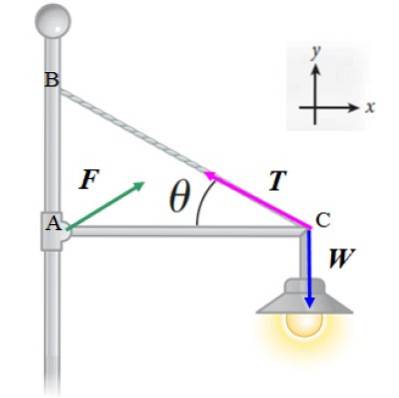
F + T + W = 0
Všimněte si, že velikost a směr F je třeba ještě určit, ale předpokládáme, že má dvě složky: FX a FY. Tímto způsobem získáme dvě rovnice:
FX -T. cos θ = 0
FY - W + T⋅ sin θ = 0
Nyní použijeme druhou rovnovážnou podmínku, zvolíme bod A, protože neznáme velikost F ani to T. Výběrem tohoto bodu vektoru rNA je null, proto okamžik F je null a velikost F se neobjeví v rovnici:
-W⋅L + T⋅sen θ⋅L = 0
Proto:
T.sen θ.L = W.L.
T = W / sin θ = (20 kg x 9,8 m / sdva) / Sin 30º = 392 N.
Když známe velikost T, můžeme ji vyřešit pro složku FX:
FX = T⋅ cos θ = 392 cos 30º N = 339. 5 N
A pak složka FY:
FY = W - T⋅ sin θ = (20 kg x 9,8 m / sdva) - 392⋅sin 30º = 0
Pak můžeme vyjádřit F Tak:
F = 339,5 N X
Jedná se tedy o horizontální sílu. Je to proto, že jsme se domnívali, že tyč měla zanedbatelnou hmotnost.
Pokud byl pro výpočet výsledného momentu zvolen bod C, vektory rT Y rŽ jsou null, proto:
M = FaL = 0
Byl vyvozen závěr, že FY = 0. Tímto způsobem:
- W + T⋅ sin θ = 0
T = W / sin θ
Což je stejný výsledek získaný původně při výběru bodu A jako místa, kde prochází osa otáčení.
Témata zájmu
Rovnovážné podmínky.
První rovnovážný stav.
Reference
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 4. Systémy částic. Upravil Douglas Figueroa (USB).
- Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. 7. Ed. Cengage Learning.



Zatím žádné komentáře