
Bernoulliho věta rovnice, aplikace a řešené cvičení
The Bernoulliho věta, který popisuje chování kapaliny v pohybu, uvedl ve své práci matematik a fyzik Daniel Bernoulli Hydrodynamika. Podle principu bude ideální tekutina (bez tření nebo viskozity), která cirkuluje uzavřeným potrubím, mít v cestě konstantní energii..
Větu lze odvodit z principu zachování energie a dokonce z druhého Newtonova pohybového zákona. Kromě toho Bernoulliho princip také stanoví, že zvýšení rychlosti kapaliny znamená snížení tlaku, kterému je vystavena, snížení její potenciální energie nebo obojí současně..

Věta má mnoho různých aplikací, a to jak ve světě vědy, tak v každodenním životě lidí..
Jeho důsledky jsou přítomné mimo jiné v zdvihací síle letadel, v komínech domů a průmyslových odvětví, ve vodovodních potrubích..
Rejstřík článků
- 1 Bernoulliho rovnice
- 1.1 Zjednodušená forma
- 2 Aplikace
- 3 Cvičení vyřešeno
- 4 Odkazy
Bernoulliho rovnice
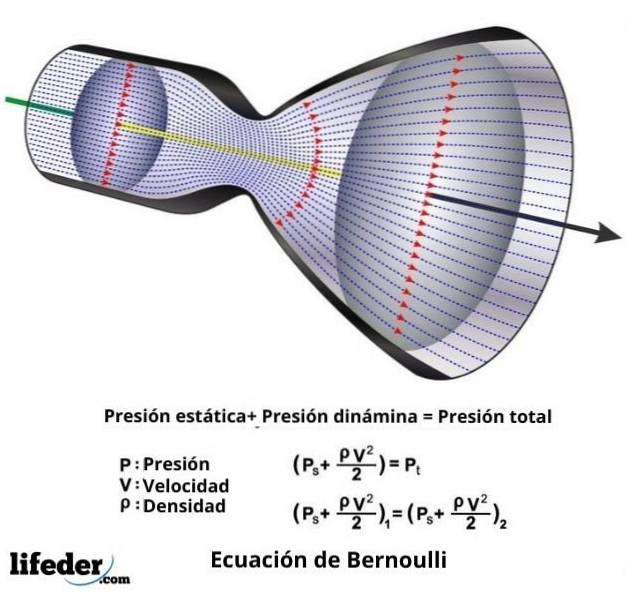
Ačkoli Bernoulli byl ten, kdo odvodil, že tlak klesá, když se zvyšuje rychlost proudění, pravdou je, že to byl Leonhard Euler, kdo ve skutečnosti vyvinul Bernoulliho rovnici v podobě, v jaké je dnes znám..
V každém případě je Bernoulliho rovnice, která není ničím jiným než matematickým vyjádřením jeho věty, následující:
protidva ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = konstanta
V tomto výrazu v je rychlost tekutiny uvažovaným řezem, ƿ je hustota tekutiny, P je tlak tekutiny, g je hodnota gravitačního zrychlení a z je výška měřená v směr gravitace.
V Bernoulliho rovnici je implicitní, že energie kapaliny se skládá ze tří složek:
- Kinetická složka, která je výsledkem rychlosti, jakou se tekutina pohybuje.
- Potenciální nebo gravitační složka, která je způsobena výškou kapaliny.
- Energie tlaku, což je energie, kterou tekutina vlastní v důsledku tlaku, kterému je vystavena.
Na druhou stranu lze Bernoulliho rovnici vyjádřit takto:
proti1 dva ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vdvadva ∙ ƿ / 2 + Pdva + ƿ ∙ g ∙ zdva
Tento poslední výraz je velmi praktický pro analýzu změn, které kapalina zažívá, když se změní některý z prvků, které tvoří rovnici.
Zjednodušená forma
Při určitých příležitostech je změna ρgz termínu Bernoulliho rovnice minimální ve srovnání s tou, kterou zažili ostatní termíny, takže ji lze zanedbávat. Například k tomu dochází v proudech, které zažívá letadlo za letu..

Při těchto příležitostech je Bernoulliho rovnice vyjádřena takto:
P + q = P0
V tomto výrazu q je dynamický tlak a odpovídá v dva ∙ ƿ / 2 a P0 je to, co se nazývá celkový tlak a je součtem statického tlaku P a dynamického tlaku q.
Aplikace

Bernoulliho věta má mnoho a různorodých aplikací v oblastech tak rozmanitých jako věda, strojírenství, sport atd..
Zajímavá aplikace se nachází v konstrukci krbů. Komíny jsou postaveny vysoko, aby se dosáhlo většího tlakového rozdílu mezi základnou a výstupem komína, díky čemuž je snazší odtah spalin.
Bernoulliho rovnice samozřejmě platí i pro studium pohybu toků kapaliny v potrubí. Z rovnice vyplývá, že zmenšení průřezu potrubí, aby se zvýšila rychlost tekutiny, která jím prochází, také znamená pokles tlaku.
Bernoulliho rovnice se používá také v letectví a ve vozidlech Formule 1. V případě letectví je Bernoulliho efekt původem vztlaku letadel.
Křídla letadel jsou navržena s cílem dosáhnout většího proudění vzduchu v horní části křídla.
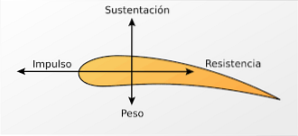
V horní části křídla je tedy rychlost vzduchu vysoká, a proto je tlak nižší. Tento tlakový rozdíl vytváří vertikálně nahoru směřující sílu (sílu zdvihu), která umožňuje letadlu vznášet se ve vzduchu. Podobného efektu se dosáhne u křidélek automobilů Formule 1.
Cvičení vyřešeno
Trubkou o průřezu 4,2 cmdva proud vody teče rychlostí 5,18 m / s. Voda klesá z výšky 9,66 m do nižší úrovně s výškou nulového převýšení, zatímco plocha průřezu trubice se zvyšuje na 7,6 cmdva.
a) Vypočítejte rychlost proudu vody na nižší úrovni.
b) Určete tlak na spodní úrovni s vědomím, že tlak na horní úrovni je 152000 Pa.
Řešení
a) Vzhledem k tomu, že tok musí být zachován, je pravda, že:
QVyšší úroveň = Qnižší úroveň
proti1 . S1 = vdva . Sdva
5,18 m / s. 4,2 cmdva = vdva . 7,6 cm ^dva
Při řešení pro se získá, že:
protidva = 2,86 m / s
b) Aplikování Bernoulliho věty mezi oběma úrovněmi a s přihlédnutím k tomu, že hustota vody je 1000 kg / m3 , získá se, že:
proti1 dva ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vdvadva ∙ ƿ / 2 + Pdva + ƿ ∙ g ∙ zdva
(1/2). 1000 kg / m3 . (5,18 m / s)dva + 152000 + 1000 kg / m3 . 10 m / sdva . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)dva + Pdva + 1000 kg / m3 . 10 m / sdva . 0 m
Řešení pro Pdva dostanete se do:
Pdva = 257926,4 Pa
Reference
- Bernoulliho princip. (n.d.). Na Wikipedii. Citováno dne 12. května 2018 z es.wikipedia.org.
- Bernoulliho princip. (n.d.). Na Wikipedii. Citováno dne 12. května 2018 z en.wikipedia.org.
- Batchelor, G.K. (1967). Úvod do dynamiky tekutin. Cambridge University Press.
- Lamb, H. (1993). Hydrodynamika (6. vydání). Cambridge University Press.
- Mott, Robert (1996). Aplikovaná mechanika tekutin (4. vydání). Mexiko: Pearson Education.


Zatím žádné komentáře