
Důkaz binomické věty a příklady
The binomická věta je rovnice, která nám říká, jak vyvinout vyjádření tvaru (a + b)n pro nějaké přirozené číslo n. Binomiál není nic jiného než součet dvou prvků, jako (a + b). Umožňuje nám to také vědět o termínu daném akbn-k jaký je koeficient, který jej doprovází.
Tato věta se běžně připisuje anglickému vynálezci, fyzikovi a matematikovi Siru Isaacovi Newtonovi; Byly však nalezeny různé záznamy, které naznačují, že jeho existence byla známa již na Středním východě, kolem roku 1000.

Rejstřík článků
- 1 Kombinatorická čísla
- 2 Demo
- 3 příklady
- 3.1 Totožnost 1
- 3.2 Totožnost 2
- 4 Další ukázka
- 4.1 Důkaz indukcí
- 5 Zajímavosti
- 6 Reference
Kombinatorická čísla
Binomická věta nám matematicky říká následující:
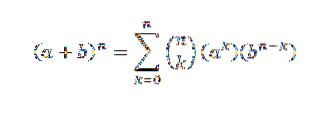
V tomto výrazu a a b jsou reálná čísla an je přirozené číslo.
Před uvedením dema se podívejme na některé základní koncepty, které jsou nezbytné.
Kombinatorické číslo nebo kombinace n v k je vyjádřeno takto:
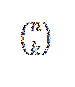
Tento formulář vyjadřuje hodnotu, kolik podmnožin s k prvky lze vybrat ze sady n prvků. Jeho algebraický výraz je dán vztahem:
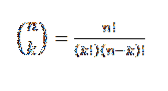
Podívejme se na příklad: Předpokládejme, že máme skupinu sedmi míčků, z nichž dvě jsou červené a ostatní jsou modré..
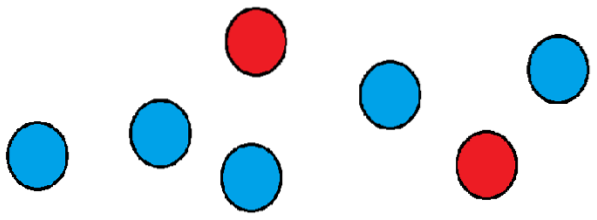
Chceme vědět, kolik způsobů je můžeme uspořádat za sebou. Jedním ze způsobů může být umístění dvou červených do první a druhé polohy a zbytek koulí do pozic, které zůstanou..
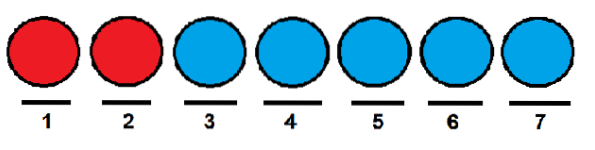
Podobně jako v předchozím případě jsme mohli dát červeným koulím první a poslední pozici a ostatní obsadit modrými koulemi.
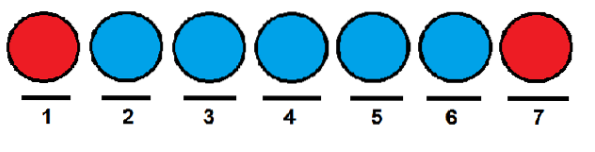
Nyní je efektivní způsob, jak spočítat, kolik způsobů můžeme uspořádat koule v řadě, pomocí kombinačních čísel. Každou pozici můžeme vidět jako prvek následující množiny:
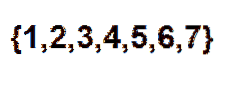
Pak zbývá jen vybrat podmnožinu dvou prvků, ve kterých každý z těchto prvků představuje pozici, kterou zaujmou červené koule. Tuto volbu můžeme provést podle vztahu daného:
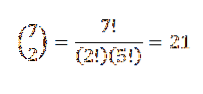
Tímto způsobem máme 21 způsobů, jak si tyto koule objednat.
Obecná myšlenka tohoto příkladu bude velmi užitečná při dokazování binomické věty. Podívejme se na konkrétní případ: pokud n = 4, máme (a + b)4, což není nic jiného než:
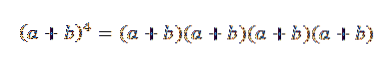
Když vyvíjíme tento produkt, zbývá nám součet podmínek získaných vynásobením jednoho prvku každého ze čtyř faktorů (a + b). Budeme tedy mít výrazy, které budou mít podobu:
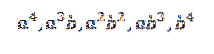
Pokud bychom chtěli získat výraz z formuláře a4, jen znásobte takto:
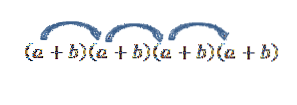
Všimněte si, že existuje pouze jeden způsob, jak tento prvek získat; ale co se stane, když nyní hledáme termín formy advabdva? Protože „a“ a „b“ jsou reálná čísla, a proto je komutativní zákon platný, existuje jeden způsob, jak tento termín získat, je znásobit členy tak, jak je naznačeno šipkami.
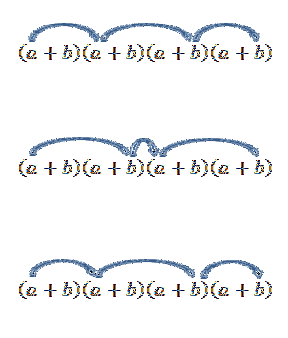
Provádění všech těchto operací je obvykle poněkud zdlouhavé, ale pokud vidíme výraz „a“ jako kombinaci, kde chceme vědět, kolik způsobů můžeme zvolit dvě „a“ ze sady čtyř faktorů, můžeme použít myšlenku z předchozí příklad. Takže máme následující:
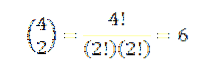
Víme tedy, že při konečném rozšíření výrazu (a + b)4 budeme mít přesně 6advabdva. Při použití stejného nápadu pro ostatní prvky musíte:
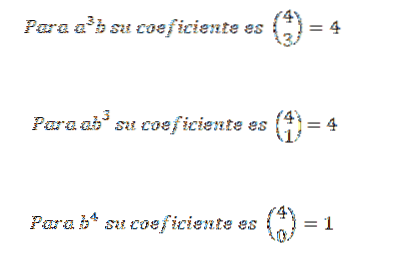
Potom přidáme dříve získané výrazy a máme to:
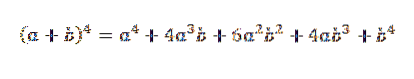
Je to formální důkaz pro obecný případ, ve kterém „n“ je jakékoli přirozené číslo.
Demonstrace
Všimněte si, že podmínky, které zůstanou při vývoji (a + b)n Jsou ve formě akbn-k, kde k = 0,1,…, n. S využitím myšlenky předchozího příkladu máme způsob, jak zvolit „k“ proměnné „a“ z „n“ faktorů je:
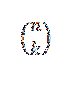
Tímto výběrem automaticky volíme n-k proměnných „b“. Z toho vyplývá, že:
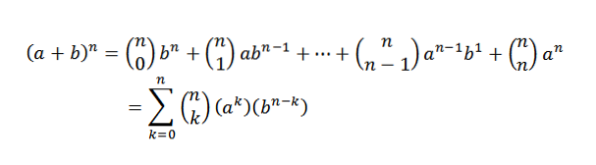
Příklady
Zvažování (a + b)5, Jaký by byl váš vývoj?
Podle binomické věty máme:
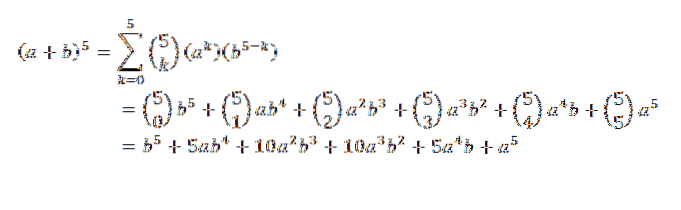
Binomická věta je velmi užitečná, máme-li výraz, ve kterém chceme vědět, jaký je koeficient konkrétního členu, aniž bychom museli provést úplnou expanzi. Jako příklad si můžeme vzít následující neznámé: jaký je koeficient x7Y9 v expanzi (x + y)16?
Podle binomické věty máme, že koeficient je:
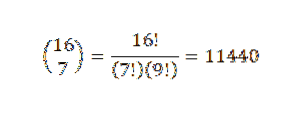
Dalším příkladem by bylo: jaký je koeficient x5Y8 ve vývoji (3x-7y)13?
Nejprve vhodným způsobem přepíšeme výraz; tohle je:
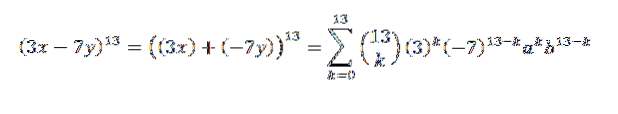
Potom pomocí binomické věty máme, že hledaný koeficient je, když máme k = 5
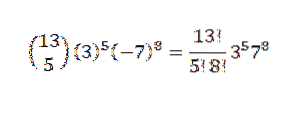
Dalším příkladem použití této věty je důkaz některých společných identit, jako jsou ty, které uvedeme níže.
Totožnost 1
Pokud je „n“ přirozené číslo, máme:
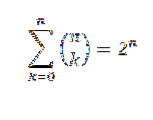
Jako důkaz použijeme binomickou větu, kde „a“ i „b“ mají hodnotu 1. Pak máme:
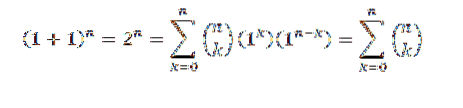
Tímto způsobem jsme prokázali první identitu.
Totožnost 2
Pokud je „n“ přirozené číslo, pak
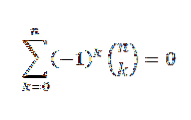
Podle binomické věty máme:
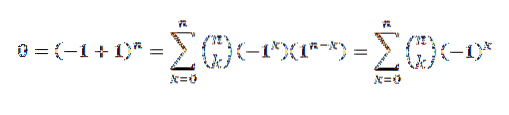
Další ukázka
Můžeme udělat jiný důkaz pro binomickou větu pomocí indukční metody a Pascalovy identity, která nám říká, že pokud jsou „n“ a „k“ kladná celá čísla, která splňují n ≥ k, pak:
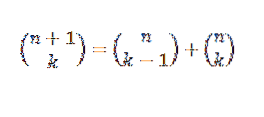
Indukční důkaz
Nejprve se podívejme, že indukční základna drží. Pokud n = 1, máme:
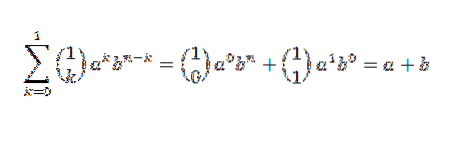
Ve skutečnosti vidíme, že je splněna. Nyní nechme n = j takové, aby:
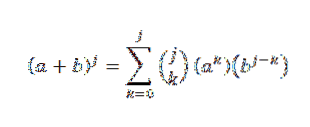
Chceme vidět, že pro n = j + 1 platí, že:
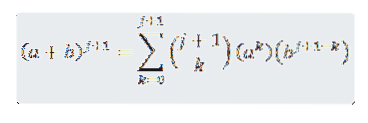
Musíme tedy:
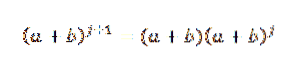
Podle hypotézy víme, že:
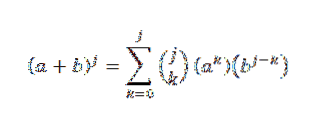
Potom pomocí distribuční vlastnosti:
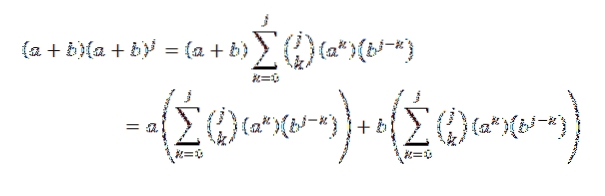
Následně při vývoji každé ze součtů máme:
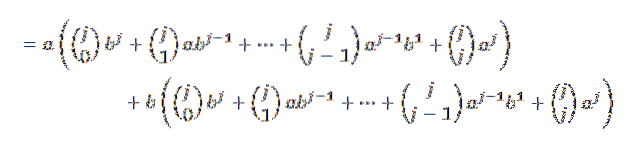
Nyní, pokud se seskupujeme pohodlným způsobem, máme to:
Pomocí identity pascalu máme:
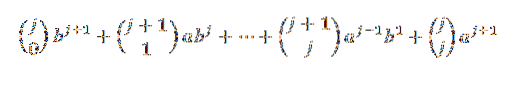
Nakonec si všimněte, že:
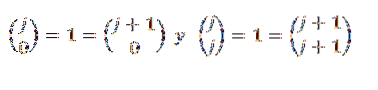
Proto vidíme, že binomická věta platí pro všechna „n“ patřící k přirozeným číslům, a tím důkaz končí.
Zajímavosti
Kombinatorické číslo (nk) se také nazývá binomický koeficient, protože je to přesně koeficient, který se objeví ve vývoji binomického čísla (a + b)n.
Isaac Newton dal zevšeobecnění této věty pro případ, ve kterém je exponent reálné číslo; tato věta je známá jako Newtonova binomická věta.
Již ve starověku byl tento výsledek znám pro konkrétní případ, ve kterém n = 2. Tento případ je zmíněn v Elementy podle Euklida.
Reference
- Johnsonbaugh Richard. Diskrétní matematika. PHH
- Kenneth.H. Rosen. Diskrétní matematika a její aplikace. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Seymour Lipschutz Ph.D & Marc Lipson. Diskrétní matematika. McGRAW-HILL.
- Ralph P. Grimaldi. Diskrétní matematika a kombinatorika. Addison-Wesley Iberoamericana
- Verde Star Luis… Diskrétní a kombinatorická matematika. Antropos



Zatím žádné komentáře