
Třetí zákon termodynamických vzorců, rovnice, příklady
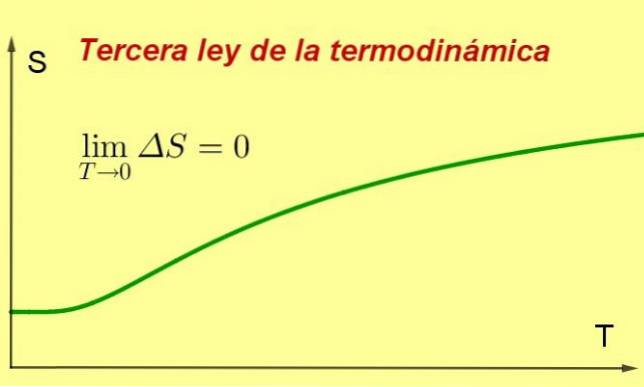
The Třetí zákon termodynamiky uvádí, že entropie uzavřeného termodynamického systému v rovnováze má tendenci být minimální a konstantní, protože se jeho teplota blíží 0 kelvinů.
Tato hodnota entropie bude nezávislá na systémových proměnných (mimo jiné tlak nebo aplikované magnetické pole). Co se stane, je to, že když se teplota blíží 0 K, procesy v systému se zastaví a protože entropie je mírou vnitřního míchání, nutně klesá.
Rejstřík článků
- 1 Předchozí koncepty
- 1.1 Termodynamický systém
- 1.2 Izolované, uzavřené nebo otevřené systémy
- 1.3 Makrostáty a mikrostavy
- 2 Vzorce a rovnice
- 2.1 Výpočet absolutní entropie látky
- 3 Aplikace
- 3.1 Entropie systému při nízké teplotě
- 3.2 Zbytková entropie
- 4 příklady
- 4.1 Příklad 1: absolutní nula a Heisenbergova neurčitost
- 4.2 Příklad 2: Superfluidita a zvláštní případ helia-4
- 5 Cvičení vyřešena
- 5.1 - Cvičení 1
- 5.2 - Cvičení 2
- 6 Reference
Předchozí koncepty
Abychom pochopili rozsah třetího termodynamického zákona, který je relevantní při velmi nízkých teplotách, je nutné přezkoumat následující pojmy:
Termodynamický systém
Obecně se jedná o plyn, kapalinu nebo pevnou látku. Nazývá se to, co není součástí systému životní prostředí. Nejběžnějším termodynamickým systémem je ideální plyn, který se skládá z N částic (atomů), které interagují pouze prostřednictvím elastických srážek.
Izolované, uzavřené nebo otevřené systémy
Izolovaným systémům není povolena žádná výměna s prostředím. Uzavřené systémy nevyměňují hmotu s prostředím, ale vyměňují teplo. A konečně, otevřené systémy mohou vyměňovat hmotu i teplo s prostředím..
Makrostáty a mikrostavy
Makrostát systému je soubor hodnot, které mají jeho proměnné: tlak, teplota, objem, počet molů, entropie a vnitřní energie. Na druhé straně je mikrostav - v případě ideálního plynu - dán polohou a hybností každé z N částic, které jej tvoří, v daném okamžiku.
Mnoho mikrostavů může mít za následek stejný makrostát. V plynu při pokojové teplotě je počet možných mikrostavů obrovský, protože počet částic, které ho tvoří, různé polohy a různé energie, které mohou přijmout, je velmi velký..
Vzorce a rovnice
Entropie, jak jsme řekli, je termodynamická makroskopická proměnná, která měří stupeň molekulární poruchy systému. Stupeň poruchy systému je větší, protože počet možných mikrostavů je větší.
Tento koncept je potřebný k formulování třetího zákona termodynamiky v matematické formě. Nechť S je entropie systému, pak:

Entropie je makroskopická stavová proměnná, která přímo souvisí s počtem možných mikrostavů systému pomocí následujícího vzorce:
S = k ln (W)
Ve výše uvedené rovnici: S představuje entropii, Ž - počet možných mikrostavů systému a - k je Boltzmannova konstanta (k = 1,38 x 10-2. 3 J / K.). To znamená, že entropie systému je k krát přirozený logaritmus počtu možných mikrostavů.
Výpočet absolutní entropie látky
Je možné definovat absolutní entropii čisté látky počínaje definicí variace entropie:

δQ = n. Cp .dT
Zde cp je molární měrné teplo an počet molů. Závislost molárního měrného tepla na teplotě jsou data získaná experimentálně a známá pro mnoho čistých látek..
Podle třetího zákona o čistých látkách:


Aplikace
V každodenním životě má třetí zákon termodynamiky málo aplikací, pravý opak prvního a druhého zákona. Je to proto, že se jedná o princip, který odkazuje na to, co se stane v systému, když se blíží absolutní 0, což je vzácný teplotní rozsah.
Ve skutečnosti není možné dosáhnout absolutní 0 nebo -273,15 ° C (viz příklad 1 níže). Třetí zákon však platí při studiu odezvy materiálů při velmi nízkých teplotách.
Díky tomu došlo ve fyzice kondenzovaných látek k významným pokrokům, jako například:
-Superfluidita (viz příklad 2 níže)
-Supravodivost
-Laserové techniky chlazení
-Bose-Einsteinův kondenzát
-Fermi superfluidní plyny.

Při extrémně nízkých teplotách umožňuje pokles entropie vznik zajímavých kvantových jevů. Podívejme se tedy, co se stane s entropií systému při velmi nízké teplotě.
Entropie systému při nízké teplotě
Když máte dokonalou krystalickou látku, její minimální entropie je přesně nula, protože se jedná o vysoce uspořádaný systém. Při teplotách blízkých absolutní hodnotě 0 je hmota v kondenzovaném stavu (kapalném nebo pevném) a vibrace v krystalu jsou minimální.
Někteří autoři považují alternativní tvrzení třetího zákona termodynamiky za následující:
„Pokud hmota kondenzuje a vytvoří dokonalý krystal, má teplota tendenci k absolutní nule, entropie má tendenci přesně k nule“.
Pojďme si vyjasnit některé aspekty předchozího prohlášení:
- Dokonalý krystal je ten, ve kterém je každá molekula identická a ve kterém se molekulární struktura opakuje identicky jako celek..
- Jak se teplota blíží absolutní nule, atomová vibrace klesá téměř úplně.
Pak krystal tvoří jedinou konfiguraci nebo možný mikrostav, tj. W = 1, a proto se entropie rovná nule:
S = k ln (1) = 0
Ale není to vždy tak, že materiál ochlazený blízko absolutní nuly tvoří krystal, natož tento krystal je dokonalý. K tomu dochází, pouze pokud je proces chlazení velmi pomalý a reverzibilní..
Jinak by faktory, jako jsou nečistoty přítomné ve skle, umožnily existenci dalších mikrostatů. Proto W> 1 a entropie by byly větší než 0.
Zbytková entropie
Pokud je proces chlazení náhlý, během něj systém prochází řadou nerovnovážných stavů, které vedou k zeskelnění materiálu. V tomto případě se nevyrábí uspořádaná krystalická struktura, ale amorfní pevná látka, jejíž struktura je podobná struktuře kapaliny..
V takovém případě není minimální hodnota entropie v blízkosti absolutní nuly nula, protože počet mikrostavů je podstatně větší než 1. Rozdíl mezi touto entropií a nulovou entropií dokonalého krystalického stavu je známý jako zbytková entropie.
Vysvětlení spočívá v tom, že pod určitou prahovou teplotou nemá systém jinou možnost, než obsadit mikrostáty nižší energií, která, protože jsou kvantovány, tvoří pevné číslo.
Postarají se o udržení konstantní entropie, i když teplota nadále klesá k absolutní nule..
Příklady
Příklad 1: absolutní nula a Heisenbergova neurčitost
Heisenbergův princip neurčitosti stanoví, že nejistota v poloze a hybnosti částice, například v atomech krystalové mřížky, nejsou na sobě nezávislé, ale spíše se řídí následující nerovností:
Δx ⋅ Δp ≥ h
Kde h je Planckova konstanta. To znamená, že nejistota v poloze vynásobená nejistotou v hybnosti (rychlost času hmoty) je větší nebo rovna Planckově konstantě, jejíž hodnota je velmi malá, ale ne nula: h = 6,63 x 10-3. 4 J s.
A co má princip neurčitosti společného s třetím zákonem termodynamiky? Pokud je poloha atomů v krystalové mřížce pevná a přesná (Δx = 0), pak rychlost těchto atomů může nabývat jakékoli hodnoty mezi 0 a nekonečnem. Tomu odporuje skutečnost, že při absolutní nule přestane veškerý pohyb tepelného míchání..
Recipročně, pokud předpokládáme, že při absolutní nulové teplotě veškeré míchání ustane a hybnost každého atomu v mřížce je přesně nula (Δp = 0), pak by Heisenbergův princip nejistoty znamenal, že neurčitost v pozicích každého atomu by byla nekonečná, to znamená, že mohou být v jakékoli poloze.
V důsledku předchozího tvrzení by počet mikrostavů měl sklon k nekonečnu a entropie by také měla neurčitou hodnotu.
Příklad 2: Superfluidita a zvláštní případ helia-4
V superfluiditě, ke které dochází při velmi nízkých teplotách, ztrácí hmota vnitřní tření mezi svými molekulami, tzv viskozita. V takovém případě by tekutina mohla cirkulovat bez tření navždy, ale problém je, že při těchto teplotách není téměř nic kapalné kromě hélia..
Helium a helium 4 (jeho nejhojnější izotop) představují jedinečný případ, protože při atmosférickém tlaku a při teplotách blízkých absolutní nule zůstává helium kapalné.
Když je hélium-4 vystaveno teplotě pod 2,2 K za atmosférického tlaku, stává se a supratekutý. K tomuto objevu došlo v roce 1911 v Leydenu nizozemským fyzikem Heike Kamerlingh Onnes (1853-1926).
Atom helia-4 je a boson. Bosony jsou na rozdíl od fermionů částice, které mohou všechny zaujímat stejný kvantový stav. Proto bosony nesplňují Pauliho princip vyloučení.
Pak všechny atomy helia-4 při teplotách pod 2,2 K zaujímají stejný kvantový stav, a proto existuje pouze jeden možný mikrostav, z čehož vyplývá, že superfluidní helium-4 má S = 0.
Vyřešená cvičení
- Cvičení 1
Uvažujme jednoduchý případ, který se skládá ze systému složeného pouze ze tří částic, které mají tři energetické úrovně. Pro tento jednoduchý systém:
a) Určete počet možných mikrostavů pro tři teplotní rozsahy:
-vysoký
-Polovina
-Krátký
b) Určete pomocí Boltzmannovy rovnice entropii v různých teplotních rozsazích.
c) Diskutujte o výsledcích a vysvětlete, zda jsou v rozporu s třetím zákonem termodynamiky..
Řešení
V molekulárním a atomovém měřítku jsou energie, které může systém přijmout, kvantovány, což znamená, že mohou přijímat pouze určité diskrétní hodnoty. Kromě toho, když jsou teploty tak nízké, mají částice, které tvoří systém, pouze možnost obsazení nejnižších energetických úrovní..
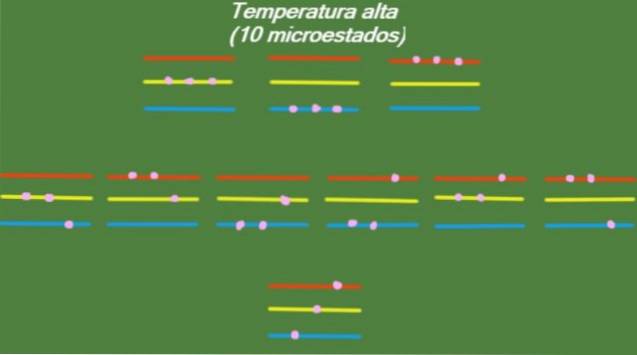
Vysoká teplota
Pokud má systém relativně vysokou teplotu T, pak mají částice dostatek energie k obsazení všech dostupných úrovní, což vede ke vzniku 10 možných mikrostavů, které se objevují na následujícím obrázku:
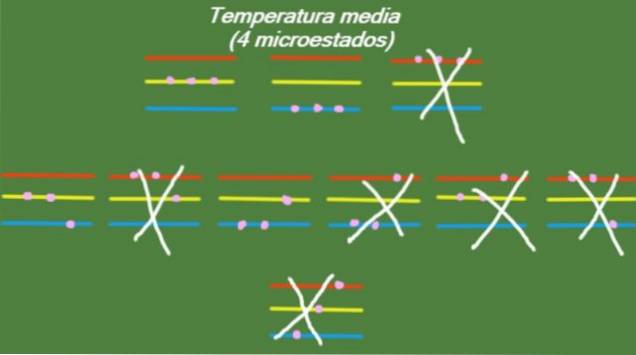
Střední teplota
V případě, že systém má střední teplotu, pak částice, které jej tvoří, nemají dostatek energie k obsazení nejvyšší energetické úrovně. Možné mikrostavy jsou znázorněny na obrázku:
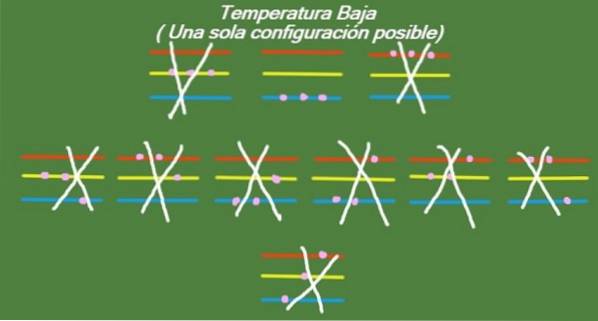
Nízká teplota
Pokud teplota v našem idealizovaném systému tří částic a tří energetických úrovní bude i nadále klesat, budou mít částice tak málo energie, že budou schopny obsadit pouze nejnižší úroveň. V takovém případě zbývá pouze 1 možný mikrostav, jak ukazuje obrázek 6:
Řešení b
Jakmile je znám počet mikrostavů v každém teplotním rozsahu, můžeme nyní použít Boltzmannovu rovnici uvedenou výše k nalezení entropie v každém případě.
S = k ln (10) = 2,30 x k = 3,18 x 10-2. 3 J / K. (Vysoká teplota)
S = k ln (4) = 1,38 x k = 1,92 x 10-2. 3 J / K. (Střední teplota)
A nakonec:
S = k ln (1) = 0 (Nízká teplota)
Řešení c
Nejprve si všimneme, že entropie podle očekávání klesá s poklesem teploty. Ale pro nejnižší hodnoty teploty je dosaženo prahové hodnoty, ze které je dosažen základní stav systému..
I když je teplota co nejblíže absolutní nule, nejsou k dispozici žádné nižší energetické stavy. Potom entropie udržuje svoji minimální hodnotu konstantní, což je v našem příkladu S = 0.
Toto cvičení ilustruje na úrovni mikrostavu systému důvod, proč platí třetí zákon termodynamiky..
- Cvičení 2
Důvod, zda je následující výrok pravdivý nebo nepravdivý:
„Entropie systému při absolutní nulové teplotě je přesně nula“.
Zdůvodněte svou odpověď a popište několik příkladů.
Řešení
Odpověď zní: nepravdivá.
Za prvé nelze dosáhnout absolutní nuly teploty, protože by to porušilo Heisenbergův princip neurčitosti a třetí zákon termodynamiky..
Je velmi důležité si uvědomit, že třetí zákon neříká, co se stane v absolutní 0, ale když je teplota nekonečně blízko absolutní 0. Rozdíl je nepatrný, ale významný.
Třetí zákon rovněž nepotvrzuje, že když teplota nabývá hodnoty libovolně blízké absolutní nule, má entropie sklon k nule. K tomu by došlo pouze v případě, který byl dříve analyzován: dokonalý krystal, který je idealizací.
Mnoho systémů v mikroskopickém měřítku, to znamená v kvantovém měřítku, má svou základní hladinu energie degenerovat, což znamená existenci různých nastavení na nejnižší energetické úrovni.
To znamená, že v těchto systémech by entropie nikdy nebyla přesně nula. Ani entropie by nebyla přesně nula v systémech, které vitrifikují, když teplota má sklon k absolutní nule. V tomto případě zbytková entropie předtím viděn.
Je to způsobeno tím, že jeho molekuly byly „zaseknuty“ před dosažením nejnižší dostupné úrovně energie, což značně zvyšuje počet možných mikrostavů, což znemožňuje, aby entropie byla přesně nula..
Reference
- Cengel, Y. 2012. Termodynamika. 7. vydání. McGraw Hill. 347.
- Laboratoř tryskového pohonu. Nejchladnější místo ve vesmíru. Citováno z: coldatomlab.jpl.nasa.gov.
- González, A. Entropie a spontánnost. Obnoveno z: geocities.ws
- Quora. Jaké je praktické využití třetího zákona termodynamiky? Obnoveno z: quora.com
- Obecná chemie. Třetí princip termodynamiky. Obnoveno z: corinto.pucp.edu.pe
- Třetí zákon termodynamiky. Obnoveno z: youtube.com
- Wikipedia. Zbytková entropie. Obnoveno z: en.wikipedia.com
- Wikipedia. Třetí zákon termodynamiky. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře