Newtonovy třetí právní aplikace, experimenty a cvičení

The Newtonův třetí zákon, také zvaný zákon akce a reakce uvádí, že když jeden objekt vyvíjí sílu na druhý, druhý také vyvíjí na první sílu stejné velikosti a směru a opačného směru.

Isaac Newton ve své knize uvedl své tři zákony známé v roce 1686 Philosophiae Naturalis Principia Mathematica o Matematické principy přírodní filozofie.

Rejstřík článků

• 1 Vysvětlení a vzorce
• 2 Aplikace
  • 2.1 Interakce míč-země
  • 2.2 Fungování rakety
  • 2.3 Používání bruslí
• 3 Experiment pro děti: bruslaře
  • 3.1 Vzorce použité v tomto příkladu
• 4 Cvičení vyřešeno
  • 4.1 Řešení
  • 4.2 Výsledky
• 5 příkladů Newtonova třetího zákona v každodenním životě
  • 5.1 Chůze
  • 5.2 Pohyb automobilu
  • 5.3 Sport
  • 5.4 Požární hadice
• 6 Reference

Vysvětlení a vzorce

Matematická formulace Newtonova třetího zákona je velmi jednoduchá:

F₁₂ = -F_{dvacet jedna}

Jedna ze sil se jmenuje akce a druhý je reakce. Je však nutné zdůraznit důležitost tohoto detailu: oba působí na různé objekty. Dělají to také současně, ačkoli tato terminologie nesprávně naznačuje, že akce nastává před a reakce po..

Protože síly jsou vektory, jsou označeny tučně. Tato rovnice naznačuje, že máme dva objekty: objekt 1 a objekt 2. Síla F₁₂ je síla vyvíjená objektem 1 na objekt 2. Síla F_{dvacet jedna} je vyvíjeno objektem 2 na objekt 1. A znaménko (-) označuje, že jsou naproti.

Při pečlivém dodržování Newtonova třetího zákona je u prvních dvou pozorován důležitý rozdíl: zatímco vyvolávají jeden objekt, třetí zákon odkazuje na dva různé objekty.

A je to tak, že pokud pečlivě myslíte, interakce vyžadují dvojice objektů.

Z tohoto důvodu se akční a reakční síly navzájem nevyrušují ani nevyvažují, i když mají stejnou velikost a směr, ale opačný směr: jsou aplikovány na různá tělesa..

Aplikace

Interakce koule a země

Zde je velmi každodenní aplikace interakce související s Newtonovým třetím zákonem: vertikálně padající koule a Země. Míč padá na zem, protože Země vyvíjí přitažlivou sílu, která se nazývá gravitace. Tato síla způsobí pád koule s konstantním zrychlením 9,8 m / s^dva.

Málokdo si však myslí, že míč také působí přitažlivou silou na Zemi. Země samozřejmě zůstává nezměněna, protože její hmotnost je mnohem větší než hmotnost koule, a proto zažívá zanedbatelné zrychlení.

Dalším pozoruhodným bodem třetího Newtonova zákona je, že kontakt mezi dvěma interagujícími objekty není nutný. Je zřejmé z právě citovaného příkladu: míč ještě nepřijal kontakt se Zemí, ale přesto přitahuje. A také koule na Zemi.

Síla, jako je gravitace, která působí nezřetelně, ať už dochází ke kontaktu mezi objekty nebo ne, se nazývá „akční síla na dálku“. Na druhou stranu síly jako tření a normály vyžadují, aby byly vzájemně se ovlivňující objekty v kontaktu, proto se jim říká „kontaktní síly“.

Vzorce převzaté z příkladu

Vrátíme-li se k dvojici objektů koule - Země, výběrem indexů P pro míč a T pro Zemi a uplatněním druhého Newtonova zákona na každého účastníka tohoto systému, získáme:

F_výsledný = m.na

Třetí zákon stanoví, že:

m_Pna_P = - m_Tna_T

na_P = 9,8 m / s^dva směřující svisle dolů. Protože k tomuto pohybu dochází ve svislém směru, je možné upustit od vektorového zápisu (tučně); a zvolením směru nahoru jako pozitivního a dolů jako negativního máme:

na_P = 9,8 m / s^dva

m_T ≈ 6 x 10 ²⁴ Kg

Bez ohledu na hmotnost koule je zrychlení Země nulové. To je důvod, proč je pozorováno, že míč padá k Zemi, a ne naopak..

Provoz rakety

Rakety jsou dobrým příkladem uplatnění Newtonova třetího zákona. Raketa zobrazená na obrázku na začátku stoupá díky pohonu horkých plynů vysokou rychlostí.

Mnoho lidí věří, že k tomu dochází, protože tyto plyny se nějak opírají o atmosféru nebo o zem, aby podporovaly a poháněly raketu. Tak to nefunguje.

Stejně jako raketa vyvíjí sílu na plyny a vypuzuje je dozadu, plyny vyvíjejí sílu na raketu, která má stejný modul, ale opačný směr. Tato síla dává raketě její zrychlení nahoru.

Pokud takovou raketu nemáte po ruce, existují další způsoby, jak zkontrolovat, že Newtonův třetí zákon funguje jako pohon. Lze postavit vodní rakety, ve kterých je potřebný tah zajištěn vodou vypuzovanou pomocí stlačeného plynu..

Je třeba poznamenat, že spuštění vodní rakety vyžaduje čas a vyžaduje mnoho opatření.

Použití bruslí

Cenově dostupnějším a okamžitým způsobem, jak zkontrolovat účinek třetího zákona Newtona, je obutí bruslí a propíchnutí o zeď..

Schopnost vyvinout sílu je většinou spojena s objekty, které jsou v pohybu, ale pravdou je, že nepohyblivé objekty mohou také vyvíjet síly. Bruslař je tlačen dozadu díky síle, kterou na něj působí nepohyblivá zeď.

Plochy ve styku vyvíjejí (normální) vzájemné kontaktní síly. Když kniha spočívá na vodorovném stole, působí na ni svislou silou, která se nazývá normální. Kniha vyvíjí na stůl vertikální sílu se stejnou číselnou hodnotou a opačným směrem.

Dětský experiment: bruslaři

Děti i dospělí mohou snadno zažít třetí Newtonův zákon a ověřit si, že akční a reakční síly se navzájem nevyrušují a jsou schopné zajišťovat pohyby..

Dva bruslaři na ledě nebo na velmi hladkém povrchu se díky zákonu akce a reakce mohou navzájem pohánět a zažít pohyby v opačném směru, ať už mají stejnou hmotnost nebo ne.

Zvažte dva bruslaře se zcela odlišnou hmotností. Jsou uprostřed kluziště se zanedbatelným třením a jsou zpočátku v klidu. V daném okamžiku se navzájem tlačili vyvíjením konstantní síly dlaněmi svých rukou. Jak se budou oba pohybovat?

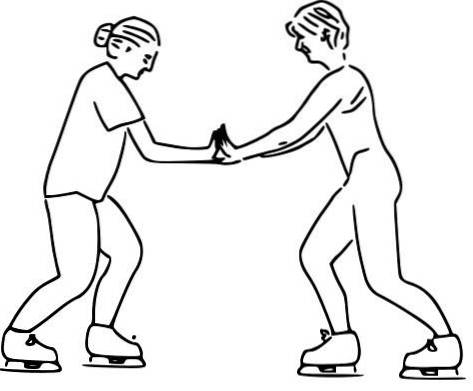
Je důležité si uvědomit, že jelikož jde o povrch bez tření, jediné nevyvážené síly jsou síly, které na sebe bruslaři působí. I když váha a normál působí na oba, tyto síly se vyrovnávají, jinak by bruslaři akcelerovali ve svislém směru.

Vzorce použité v tomto příkladu

Třetí Newtonův zákon stanoví, že:

F₁₂ = -F_{dvacet jedna}

To znamená, že síla vyvíjená bruslařem 1 na 2 má stejnou velikost jako síla vyvíjená 2 na 1, se stejným směrem a opačným směrem. Všimněte si, že tyto síly jsou aplikovány na různé objekty stejným způsobem, jakým byly síly aplikovány na kouli a Zemi v předchozím koncepčním příkladu..

m₁ na₁ = -m_dva na_dva

Jelikož jsou síly opačné, zrychlení, která způsobují, budou také opačná, ale jejich velikosti se budou lišit, protože každý bruslař má jinou hmotnost. Podívejme se na zrychlení, které získal první bruslař:

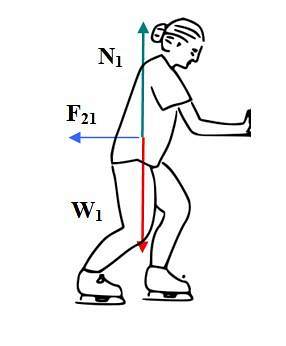
Dalším pohybem je tedy oddělení obou bruslařů v opačných směrech. Bruslaři byli v zásadě v klidu uprostřed trati. Každý vyvíjí na druhého sílu, která zajišťuje zrychlení, pokud jsou ruce v kontaktu a tlak trvá.

Poté se bruslaři od sebe vzdálili rovnoměrným přímočarým pohybem, protože nevyvážené síly již nepůsobily. Rychlost každého bruslaře se bude lišit, pokud bude také jejich hmotnost.

Cvičení vyřešeno

K řešení problémů, při nichž musí být aplikovány Newtonovy zákony, je nutné opatrně nakreslit síly působící na objekt. Tento výkres se nazývá „diagram volného těla“ nebo „diagram izolovaného těla“. Síly vyvíjené tělem na jiné objekty by v tomto diagramu neměly být zobrazeny..

Pokud se na problému podílí více než jeden objekt, je nutné pro každý z objektů nakreslit diagram volného těla, přičemž si pamatujte, že akční-reakční páry působí na různá těla..

1- Bruslaři předchozí části mají příslušné hmotnosti m₁ = 50 kg a m_dva = 80 kg. Tlačí se navzájem konstantní silou 200 N. Tlak trvá 0,40 sekundy. Nalézt:

a) Zrychlení, které každý bruslař získá díky tahu.

b) Rychlost každého vstupu, když se rozdělí

Řešení

a) Vezměte jako pozitivní horizontální směr ten, který jde zleva doprava. Při použití druhého Newtonova zákona s hodnotami uvedenými v prohlášení máme:

F_{dvacet jedna} = m₁na₁

Odkud:

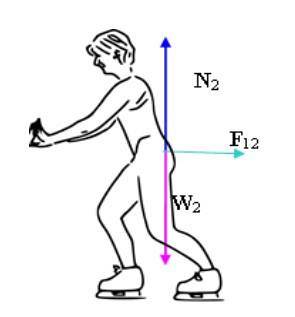
Pro druhého bruslaře:

b) Pro výpočet rychlosti, kterou přenášejí právě při separaci, se používají kinematické rovnice rovnoměrně zrychleného přímočarého pohybu:

Počáteční rychlost je 0, protože byly v klidu uprostřed stopy:

proti_F = v

proti_f1 = a₁t = -4 m / s^dva . 0,40 s = -1,6 m / s

proti_f2 = a_dvat = +2,5 m / s^dva . 0,40 s = +1 m / s

Výsledek

Jak se dalo očekávat, osoba 1, která je lehčí, získává větší zrychlení, a proto vyšší rychlost. Nyní si povšimněte následujícího o součinu hmotnosti a rychlosti každého bruslaře:

m₁ proti₁ = 50 kg. (-1,6 m / s) = - 80 kg.m / s

m_dva proti_dva = 80 kg. 1 m / s = +80 kg.m / s

Součet obou součinů je 0. Součin hmotnosti a rychlosti se nazývá hybnost P. Je to vektor se stejným směrem a smyslem pro rychlost. Když byli bruslaři v klidu a jejich ruce byly v kontaktu, dalo se předpokládat, že vytvořily stejný objekt, jehož hybnost byla:

P_nebo = (m₁ +m_dva) v_nebo = 0

Po skončení tlačení zůstává množství pohybu bruslařského systému 0. Proto je množství pohybu zachováno.

Příklady třetího Newtonova zákona v každodenním životě

Na procházku

Chůze je jednou z nejvíce každodenních činností, které lze provádět. Při pečlivém pozorování vyžaduje činnost chůze tlačit nohu proti zemi, takže vrací stejnou a opačnou sílu na nohu chodítka..

Právě tato síla umožňuje lidem chodit. Během letu ptáci vyvíjejí sílu na vzduch a vzduch tlačí křídla tak, aby se pták pohnul dopředu.

Pohyb auta

V automobilu působí kola na chodník. Díky reakci chodníku vyvíjí síly na pneumatiky, které pohánějí auto vpřed.

Sport

Ve sportu jsou síly akce a reakce četné a mají velmi aktivní účast.

Podívejme se například na sportovce s nohou položenou na startovacím bloku. Blok poskytuje normální sílu v reakci na tlak, který na něj sportovec vyvíjí. Výsledek této normály a hmotnosti běžce má za následek horizontální sílu, která umožňuje sportovi pohánět se dopředu..

Požární hadice

Dalším příkladem, kde je přítomen Newtonův zákon, jsou hasiči, kteří drží požární hadice. Konec těchto velkých hadic má rukojeť na trysce, kterou musí hasič držet, když proudí voda, aby se zabránilo zpětnému rázu, ke kterému dochází, když voda proudí.

Ze stejného důvodu je vhodné uvázat čluny k doku před jejich opuštěním, protože když se tlačí k doku, působí na člun síla, která jej od něj vzdaluje..

Reference

1. Giancoli, D. 2006. Fyzika: Principy s aplikacemi. Šesté vydání. Prentice Hall. 80 - 82.
2. Rex, A. 2011. Základy fyziky. Pearson. 73 - 75.
3. Tipler, P. 2010. Fyzika. Svazek 1. 5. vydání. Redakční reverté. 94 - 95.
4. Stern, D. 2002. Od astronomů po kosmické lodě. Převzato z: pwg.gsfc.nasa.gov.