Parabolické střelecké vlastnosti, vzorce a rovnice, příklady

The parabolický výstřel Skládá se z házení předmětu nebo střely pod určitým úhlem a jejího ponechání v pohybu působením gravitace. Pokud není brán v úvahu odpor vzduchu, bude objekt bez ohledu na jeho povahu sledovat dráhu oblouku paraboly.

Je to každodenní pohyb, protože mezi nejoblíbenější sporty patří ty, ve kterých se hází míčky nebo míčky, ať už rukou, nohou nebo například nástrojem, jako je raketa nebo pálka..

Pro jeho studium je parabolický výstřel rozdělen na dva superponované pohyby: jeden horizontální bez zrychlení a druhý vertikální s konstantním zrychlením dolů, což je gravitace. Oba pohyby mají počáteční rychlost.

Řekněme, že vodorovný pohyb probíhá podél osy x a svislý pohyb podél osy y. Každý z těchto pohybů je na sobě nezávislý.

Protože určování polohy střely je hlavním cílem, je nutné zvolit vhodný referenční systém. Podrobnosti jsou uvedeny níže.

Rejstřík článků

• 1 Parabolické brokové vzorce a rovnice
  • 1.1 - Trajektorie, maximální výška, maximální čas a horizontální dosah
• 2 Příklady parabolické střelby
  • 2.1 Parabolická střelba v lidské činnosti
  • 2.2 Parabolický výstřel v přírodě
• 3 Cvičení
• 4 Odkazy

Parabolické brokové vzorce a rovnice

Předpokládejme, že je objekt hozen s úhlem α vzhledem k horizontální a počáteční rychlosti proti_nebo jak je znázorněno na obrázku doleva. Parabolický výstřel je pohyb, který se odehrává v letadle xy a v takovém případě se počáteční rychlost rozpadne takto:

proti_vůl = v_nebo cos α

proti_Ahoj = v_nebo hřích α

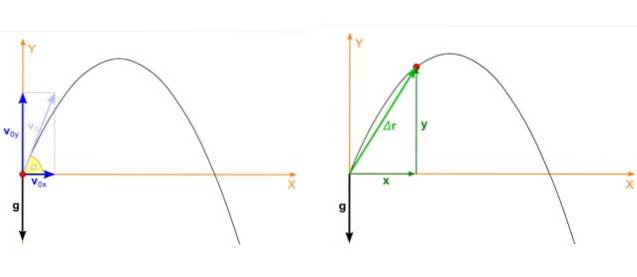
Poloha střely, což je červená tečka na obrázku 2, pravý obrázek, má také dvě časově závislé složky, jednu v X a druhý v Y. Pozice je vektor označený jako r a jeho jednotky jsou délka.

Na obrázku se počáteční poloha střely shoduje s počátkem souřadnicového systému, tedy x_nebo = 0 a_nebo = 0. To neplatí vždy, počátek můžete zvolit kdekoli, ale tato volba značně zjednodušuje výpočty.

Pokud jde o dva pohyby v x a v y, jedná se o:

-x (t): je rovnoměrný přímočarý pohyb.

-y (t): odpovídá rovnoměrně zrychlenému přímočarému pohybu s g = 9,8 m / s^dva a směřuje svisle dolů.

V matematické formě:

x (t) = v_nebo cos α.t

y (t) = v_nebo .hřích α.t - ½ g.t^dva

Vektor polohy je:

r (t) = [v_nebo cos α.t]i + [proti_nebo .hřích α.t - ½ g.t^dva] j

V těchto rovnicích si pozorný čtenář všimne, že znaménko mínus je způsobeno gravitací směřující k zemi, směr zvolený jako záporný, zatímco nahoru je považován za kladný..

Protože rychlost je první derivací polohy, jednoduše ji odvodíme r t) s ohledem na čas a získat:

proti (t) = v_nebo cos α i + (proti_nebo .hřích α - gt) j

Nakonec je zrychlení vyjádřeno vektorově jako:

na (t) = -g j

- Trajektorie, maximální výška, maximální čas a horizontální dosah

Trajektorie

Abychom našli explicitní rovnici cesty, kterou je křivka y (x), musíme eliminovat časový parametr, řešení v rovnici pro x (t) a dosazení v y (t). Zjednodušení je poněkud pracné, ale nakonec získáte:

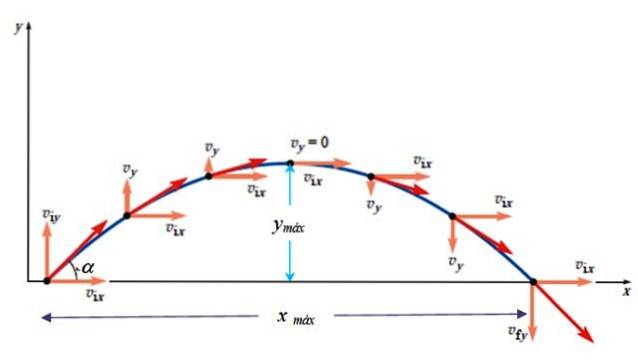
Maximální výška

Maximální výška nastane, když proti_Y = 0. S vědomím, že mezi polohou a druhou mocninou rychlosti existuje následující vztah:

proti_Y^dva = v_Ahoj ^dva- 2gy

Dělá proti_Y = 0 při dosažení maximální výšky:

0 = v_Ahoj ^dva- 2g. A_max → a_max = v_Ahoj ^dva/ 2 g

S:

proti_Ahoj = v_nebo senα

Maximální čas

Maximální čas je čas potřebný k dosažení objektu a_max. K výpočtu se používá:

proti_Y = v_nebo .hřích α - gt

To vím proti_Y se stane 0, když t = t_max, výsledek:

proti_nebo .hřích α - g.t._max = 0

t_max = v_Ahoj / g

Maximální horizontální dosah a doba letu

Dosah je velmi důležitý, protože signalizuje, kam předmět spadne. Tímto způsobem budeme vědět, zda zasáhne cíl nebo ne. Abychom to našli, potřebujeme čas letu, celkový čas nebo t_proti.

Z výše uvedeného obrázku lze snadno usoudit, že t_proti = 2. t_max. Ale buďte opatrní! To platí pouze v případě, že je start rovný, to znamená, že výška počátečního bodu je stejná jako výška příjezdu. Jinak je čas nalezen řešením kvadratické rovnice, která je výsledkem nahrazení konečné polohy Y_finále:

Y_finále = v_nebo .hřích α.t_proti - ½ g.t._proti^dva

V každém případě je maximální horizontální dosah:

X_max = v_vůl. t_proti

Příklady parabolické střelby

Parabolická střelba je součástí pohybu lidí a zvířat. Také téměř u všech sportů a her, kde dochází k gravitaci. Například:

Parabolická střelba v lidské činnosti

-Kámen hodený katapultem.

-Brankový kop brankáře.

-Míč hozený nadhazovačem.

-Šíp, který vychází z luku.

-Všechny druhy skoků

-Hodit kámen pomocí praku.

-Jakákoli hozená zbraň.

Parabolický výstřel v přírodě

-Voda, která tryská z přírodních nebo umělých trysek, například z fontány.

-Kameny a láva tryskající ze sopky.

-Míč, který se odrazí od chodníku, nebo kámen, který se odrazí od vody.

-Všechny druhy skákajících zvířat: klokani, delfíni, gazely, kočky, žáby, králíci nebo hmyz, abychom jmenovali alespoň některé.

Cvičení

Kobylka skáče pod úhlem 55 ° s vodorovnou rovinou a přistává 0,80 metru dopředu. Nalézt:

a) Dosažena maximální výška.

b) Kdyby skočil stejnou počáteční rychlostí, ale utvořil úhel 45 °, šel by výše??

c) Co lze říci o maximálním horizontálním dosahu pro tento úhel?

Řešení

Když data dodaná problémem neobsahují počáteční rychlost v_nebo výpočty jsou poněkud pracnější, ale ze známých rovnic lze odvodit nový výraz. Začínající od:

X_max = v_vůl . t_let = v_nebo.cos α. t_proti

Když přistane později, výška se vrátí na 0, takže:

proti_nebo .hřích α.t_proti - ½ g.t._proti^dva= 0

Co t_proti je společný faktor, je zjednodušený:

proti_nebo .hřích α - ½ g.t._proti= 0

Můžeme vyčistit t_proti z první rovnice:

t_proti = x_max / v_nebo.cos α

A nahradit ve druhém:

proti_nebo .hřích α - (½ g.x_max / v_nebo.cos α) = 0

Vynásobením všech výrazů číslem proti_nebo.cos αvýraz se nezmění a jmenovatel zmizí:

(proti_nebo .hřích α.) (proti_nebo.cos α) - ½g.x_max = 0

proti_nebo^dva hřích α. cos α = ½g.x_max

Už to lze vyčistit v_nebo nebo také nahraďte následující identitu:

sin 2α = 2 sin α. cos α → v_nebo^dva hřích 2α = g.x._max

Vypočítává se proti_nebo^dva:

proti_nebo^dva = g.X_max / hřích 2α = (9,8 x 0,8 / hřích 110) m^dva/ s^dva = 8,34 m^dva/ s^dva

A konečně maximální výška:

Y_max= v_Ahoj ^dva/ 2 g = (8,34 x hřích^dva 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Řešení b

Humr dokáže udržet stejnou vodorovnou rychlost, ale zmenšením úhlu:

Y_max= v_Ahoj ^dva/ 2 g = (8,34 x hřích^dva 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Dosáhne nižší výšky.

Řešení c

Maximální horizontální dosah je:

X_max = v_nebo^dva sen 2. / G

Změnou úhlu se změní také vodorovný dosah:

X_max = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Skok je nyní delší. Čtečka může ověřit, že je maximální pro úhel 45 °, protože:

hřích 2α = hřích 90 = 1.

Reference

1. Figueroa, D. 2005. Řada: Fyzika pro vědy a inženýrství. Svazek 1. Kinematika. Upravil Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fyzika. Druhé vydání. Mcgraw kopec.
3. Giancoli, D. 2006. Fyzika: Principy s aplikacemi. 6.. Hala Ed Prentice.
4. Resnick, R. 1999. Fyzika. Sv. 1. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. autor: C.V.
5. Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.