Charakteristiky a typy akutního trojúhelníku

The ostré trojúhelníky jsou ty, jejichž tři vnitřní úhly jsou ostré úhly; to znamená, že míra každého z těchto úhlů je menší než 90 °. Tím, že nemáme pravý úhel, máme, že Pythagorova věta pro tento geometrický útvar neplatí.

Pokud tedy chceme mít nějaký typ informací o kterékoli z jeho stran nebo úhlů, je nutné využít další věty, které nám umožňují přístup k uvedeným datům. Můžeme použít sinusovou a kosinusovou větu.

Rejstřík článků

• 1 Funkce
  • 1.1 Sinusova věta
  • 1.2 Kosinová věta
• 2 druhy
  • 2.1 Rovnostranné ostré trojúhelníky
  • 2.2 Rovnoramenné akutní trojúhelníky
  • 2.3 Scalenové akutní trojúhelníky
• 3 Rozlišení ostrých trojúhelníků
  • 3.1 Příklad 1
  • 3.2 Příklad 2

Vlastnosti

Z charakteristik, které tento geometrický útvar má, můžeme vyzdvihnout ty, které jsou dány prostou skutečností, že je trojúhelník. Mezi nimi máme:

- Trojúhelník je mnohoúhelník, který má tři strany a tři úhly.

- Součet jeho tří vnitřních úhlů se rovná 180 °.

- Součet dvou jeho stran je vždy větší než třetí.

Jako příklad se podívejme na následující trojúhelník ABC. Obecně identifikujeme jeho strany malým písmenem a jeho úhly velkým písmenem, takže jedna strana a její protilehlý úhel mají stejné písmeno.

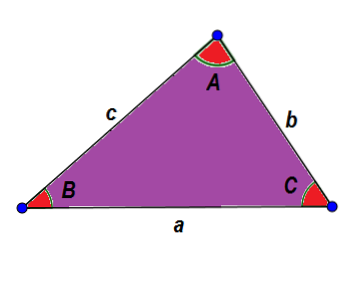
Z již uvedených charakteristik víme, že:

A + B + C = 180 °

a + b> c, a + c> b a b + c> a

Hlavní charakteristikou, která odlišuje tento typ trojúhelníku od ostatních, je to, že jak jsme již zmínili, jeho vnitřní úhly jsou ostré; to znamená, že míra každého z jeho úhlů je menší než 90 °.

Akutní trojúhelníky spolu s tupými trojúhelníky (ty, ve kterých má jeden z jejich úhlů míru větší než 90 °), jsou součástí sady šikmých trojúhelníků. Tato sada je tvořena trojúhelníky, které nejsou pravými úhly.

Jelikož jsou šikmé trojúhelníky součástí, musíme být schopni řešit problémy s akutními trojúhelníky, musíme využít sinusovou větu a kosinusovou větu.

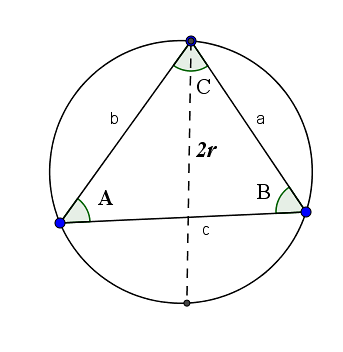
Sinusova věta

Sinusová věta nám říká, že poměr strany k sinu jeho opačného úhlu se rovná dvojnásobku poloměru kruhu tvořeného třemi vrcholy uvedeného trojúhelníku. A to:

2r = a / sin (A) = b / sin (B) = c / sin (C)

Kosinová věta

Na druhou stranu, kosinová věta nám dává tyto tři rovnosti pro jakýkoli trojúhelník ABC:

na^dva= b^dva + C^dva -2 bc * cos (A)

b^dva= a^dva + C^dva -2ac * cos (B)

C^dva= a^dva + b^dva -2ab * cos (C)

Tyto věty jsou také známé jako zákon o sinu a zákon o kosinu..

Další charakteristikou, kterou můžeme dát akutním trojúhelníkům, je to, že dva z nich jsou si rovny, pokud splňují některé z následujících kritérií:

- Pokud mají všechny tři stejné strany.

- Pokud mají jednu stranu a dva stejné úhly k sobě navzájem.

- Pokud mají dvě stejné strany a úhel.

Typy

Můžeme klasifikovat akutní trojúhelníky na základě jejich stran. Mohou to být:

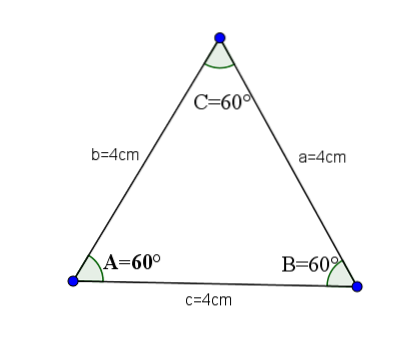
Rovnostranné ostré trojúhelníky

Jsou to akutní trojúhelníky, které mají všechny strany stejné, a proto mají všechny jejich vnitřní úhly stejnou hodnotu, což je A = B = C = 60 ° stupňů.

Jako příklad si vezměme následující trojúhelník, jehož strany a, bac mají hodnotu 4.

Rovnoramenné akutní trojúhelníky

Tyto trojúhelníky, kromě toho, že mají ostré vnitřní úhly, mají tu vlastnost, že mají dvě ze svých stejných stran a třetí, která je obecně brána jako základ, odlišná.

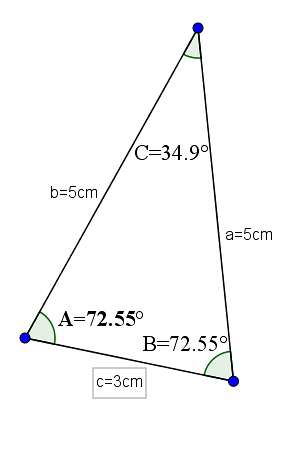
Příkladem tohoto typu trojúhelníku může být ten, jehož základna je 3 a jeho další dvě strany mají hodnotu 5. S těmito měřeními by měl opačné úhly než stejné strany s hodnotou 72,55 ° a opačný úhel základna by byla 34,9 °.

Scalene akutní trojúhelníky

Jedná se o trojúhelníky, které mají všechny různé strany dvě po druhé. Proto jsou všechny jeho úhly, kromě toho, že jsou menší než 90 °, odlišné od dvou do dvou.

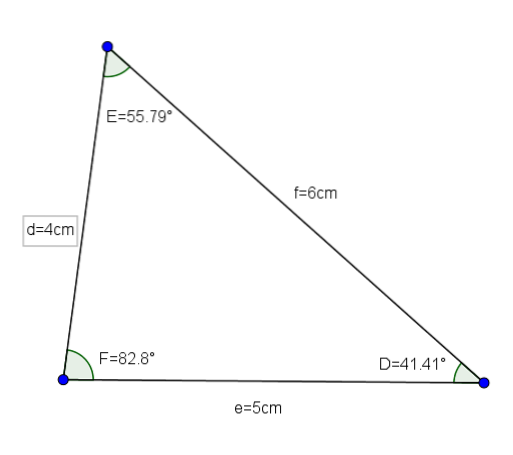
Trojúhelník DEF (jehož míry jsou d = 4, e = 5 af = 6 a jeho úhly jsou D = 41,41 °, E = 55,79 ° a F = 82,8 °) je dobrým příkladem akutního trojúhelníkového scalenu.

Rozlišení ostrých trojúhelníků

Jak jsme již řekli, k řešení problémů s akutními trojúhelníky je nutné použít věty o sinu a kosinu.

Příklad 1

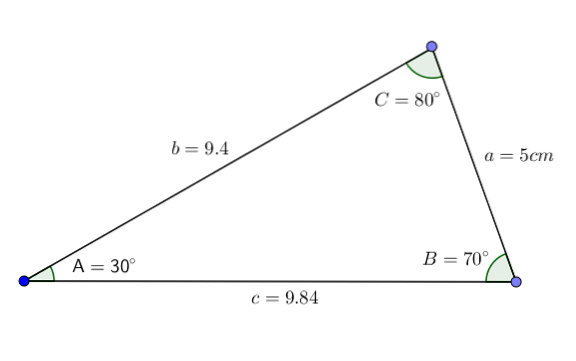
Vzhledem k trojúhelníku ABC s úhly A = 30 °, B = 70 ° a stranou a = 5 cm chceme znát hodnotu úhlu C a stran b a c.

První věc, kterou uděláme, je použít skutečnost, že součet vnitřních úhlů trojúhelníku je 180 °, abychom získali hodnotu úhlu C.

180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C

Vyčistíme C a zbývá nám:

C = 180 ° - 100 ° = 80 °

Jelikož již známe tři úhly a jednu stranu, můžeme pomocí sinusové věty určit hodnotu zbývajících stran. Podle věty máme:

a / sin (A) = b / sin (B) a a / sin (A) = c / (sin (C)

Izolujeme b z rovnice a zbývá nám:

b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4

Nyní musíme pouze vypočítat hodnotu c. Postupujeme stejně jako v předchozím případě:

c = (a * sin (C)) / sin (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84

Tím získáme všechna data trojúhelníku. Jak můžeme vidět, tento trojúhelník spadá do kategorie akutního trojúhelníku scalene.

Příklad 2

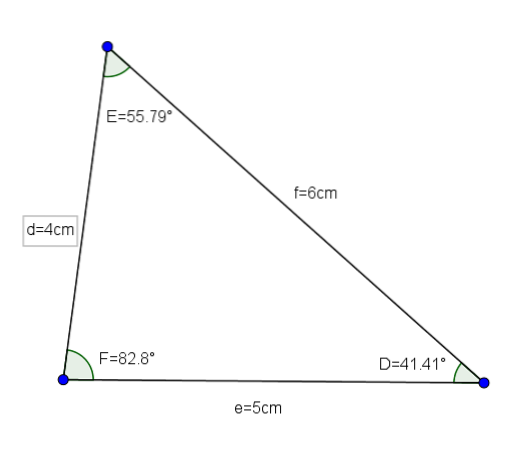
Vzhledem k trojúhelníku DEF se stranami d = 4 cm, e = 5 cm af = 6 cm chceme znát hodnotu úhlů uvedeného trojúhelníku.

V tomto případě použijeme kosinový zákon, který nám říká, že:

d^dva= e^dva + F^dva - 2efcos (D)

Z této rovnice můžeme vyřešit pro cos (D), což nám dá jako výsledek:

Cos (D) = ((4)^dva - (5)^dva -(6)^dva) / (- 2 * 5 * 6) = 0,75

Proto máme D≈ 41,41 °

Nyní pomocí věty o senom máme následující rovnici:

d / (sin (D) = e / (sin (E)

Při řešení hříchu (E) máme:

sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ≈ 0,827

Proto máme E≈55,79 °

Nakonec, když použijeme součet vnitřních úhlů trojúhelníku 180 °, máme F≈82,8 °.

1. Landaverde, F. d. (1997). Geometry (dotisk ed.). Pokrok.
2. Leake, D. (2006). Trojúhelníky (ilustrované vydání). Heinemann-Raintree.
3. Leal G. Juan Manuel. (2003). Rovinná metrická geometrie. CODEPRE
4. Ruiz, Á., & Barrantes, H. (2006). Geometrie. CR technologie.
5. Sullivan, M. (1997). Trigonometrie a analytická geometrie. Pearson Education.