Charakteristiky rovnoramenného trojúhelníku, vzorec a plocha, výpočet

A rovnoramenný trojúhelník je mnohoúhelník se třemi stranami, kde dvě z nich mají stejnou míru a třetí strana jinou míru. Tato poslední strana se nazývá základna. Díky této vlastnosti dostal toto jméno, které v řečtině znamená „stejné nohy“

Trojúhelníky jsou polygony považované za nejjednodušší v geometrii, protože jsou tvořeny třemi stranami, třemi úhly a třemi vrcholy. Jsou to ty, které mají nejmenší počet stran a úhlů vzhledem k ostatním polygonům, ale jejich použití je velmi rozsáhlé.

Rejstřík článků

• 1 Charakteristika rovnoramenných trojúhelníků
  • 1.1 Součásti
• 2 Vlastnosti
  • 2.1 Vnitřní úhly
  • 2.2 Součet stran
  • 2.3 Shodné strany
  • 2.4 Shodné úhly
  • 2.5 Výška, medián, půlící čára a půlící čára jsou shodné
  • 2.6 Relativní výšky
  • 2.7 Náhodný orthocenter, barycenter, incenter a circumcenter
• 3 Jak vypočítat obvod?
• 4 Jak vypočítat výšku?
• 5 Jak vypočítat plochu?
• 6 Jak vypočítat základnu trojúhelníku?
• 7 cvičení
  • 7.1 První cvičení
  • 7.2 Druhé cvičení
  • 7.3 Třetí cvičení
• 8 Reference

Charakteristika rovnoramenných trojúhelníků

Rovnoramenný trojúhelník byl klasifikován pomocí míry jeho stran jako parametru, protože dvě jeho strany jsou shodné (mají stejnou délku).

Na základě amplitudy vnitřních úhlů jsou rovnoramenné trojúhelníky klasifikovány jako:

• Rovnoramenný pravý trojúhelník: dvě jeho strany jsou stejné. Jeden z jeho úhlů je pravý (90^nebo) a ostatní jsou stejní (45^nebo každý)
• Rovnoramenný tupý trojúhelník: dvě jeho strany jsou stejné. Jeden z jeho úhlů je tupý (> 90^nebo).
• Rovnoramenný akutní trojúhelník: dvě jeho strany jsou stejné. Všechny jeho úhly jsou ostré (< 90^nebo), kde dva mají stejnou míru.

Komponenty

• Medián: je přímka, která začíná od středu jedné strany a dosahuje opačného vrcholu. Tyto tři mediány se sbíhají v bodě zvaném barycentrum nebo těžiště..
• Bisector: je paprsek, který rozděluje úhel každého vrcholu na dva úhly stejné míry. Proto je známá jako osa symetrie a tento typ trojúhelníků má pouze jednu.
• Prostřední: je segment kolmý na stranu trojúhelníku, který má svůj počátek ve středu trojúhelníku. Existují tři léky v trojúhelníku a setkávají se v bodě zvaném circumcenter.
• Výška: je přímka, která vede z vrcholu na stranu, která je naproti, a také tato přímka je kolmá na tuto stranu. Všechny trojúhelníky mají tři výšky, které se shodují v bodě zvaném orthocenter..

Vlastnosti

Rovnoramenné trojúhelníky jsou definovány nebo identifikovány, protože mají několik vlastností, které je reprezentují, pocházející z vět navrhovaných velkými matematiky:

Vnitřní úhly

Součet vnitřních úhlů se vždy rovná 180^nebo.

Součet stran

Součet měr dvou stran musí být vždy větší než míra třetí strany, a + b> c.

Shodné strany

Rovnoramenné trojúhelníky mají dvě strany se stejnou mírou nebo délkou; to znamená, že jsou shodní a třetí strana se od nich liší.

Shodné úhly

Rovnoramenné trojúhelníky jsou známé také jako izoanglové trojúhelníky, protože mají dva úhly, které mají stejnou míru (shodnou). Ty jsou umístěny ve spodní části trojúhelníku, naproti stranám, které mají stejnou délku.

Z tohoto důvodu byla vygenerována věta, která uvádí, že:

„Pokud má trojúhelník dvě shodné strany, budou shodné také úhly protilehlé k těmto stranám.“ Pokud je tedy trojúhelník rovnoramenný, jsou úhly jeho základen shodné.

Příklad:

Následující obrázek ukazuje trojúhelník ABC. Nakreslením jeho půlové osy z vrcholu úhlu B k základně se trojúhelník rozdělí na dva stejné trojúhelníky BDA a BDC:

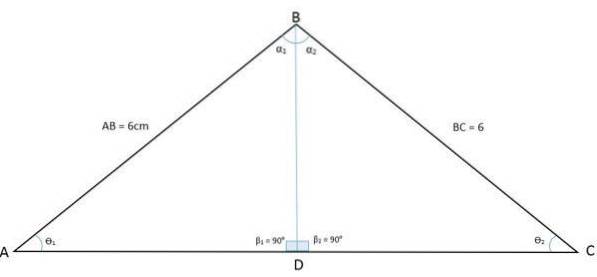
Tímto způsobem byl úhel vrcholu B také rozdělen na dva stejné úhly. Oseč je nyní společná strana (BD) mezi těmito dvěma novými trojúhelníky, zatímco strany AB a BC jsou shodné strany. Máme tedy případ kongruence strana, úhel, strana (LAL).

To ukazuje, že úhly vrcholů A a C mají stejnou míru, stejně jako je možné ukázat, že protože trojúhelníky BDA a BDC jsou shodné, strany AD a DC jsou rovněž shodné..

Výška, medián, půlící čára a půlící čára jsou shodné

Přímka, která je nakreslena od vrcholu naproti základně ke středu základny rovnoramenného trojúhelníku, je současně výškou, středem a půlící částí, stejně jako půlící částí vzhledem k opačnému úhlu základny..

Všechny tyto segmenty se shodují v jednom, který je představuje.

Příklad:

Následující obrázek ukazuje trojúhelník ABC se středem M, který rozděluje základnu na dva segmenty BM a CM.

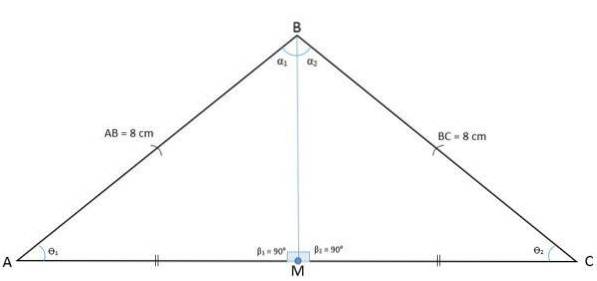
Nakreslením segmentu z bodu M na protilehlý vrchol se podle definice získá střední AM, který je relativní k vrcholu A a straně BC.

Vzhledem k tomu, že segment AM rozděluje trojúhelník ABC na dva stejné trojúhelníky AMB a AMC, znamená to, že případ kongruenční strany, úhlu, strany bude mít, a proto bude AM také půlící částí BÂC.

Proto se půlící čára vždy rovná mediánu a naopak..

Segment AM vytváří úhly, které mají stejnou míru pro trojúhelníky AMB a AMC; to znamená, že jsou doplňkové takovým způsobem, že míra každého z nich bude:

Med. (AMB) + Med. (AMC) = 180^nebo

dva _* Med. (AMC) = 180^nebo

Med. (AMC) = 180^nebo ÷ 2

Med. (AMC) = 90^nebo

Je známo, že úhly tvořené segmentem AM vzhledem k základně trojúhelníku jsou pravé, což naznačuje, že tento segment je zcela kolmý k základně..

Proto představuje výšku a půlící čáru s vědomím, že M je střed.

Proto řádek AM:

• Představuje ve výšce BC.
• Je střední velikosti.
• Je obsažen v půli BC.
• Je to půlící úhel úhlu vrcholu Â

Relativní výšky

Výšky, které jsou relativní ke stejným stranám, mají také stejné měření.

Vzhledem k tomu, že rovnoramenný trojúhelník má dvě stejné strany, budou jejich dvě příslušné výšky také stejné..

Ortocentrum, barycentrum, incenter a shodný circumcenter

Vzhledem k tomu, že výška, medián, přímka a přímka vzhledem k základně jsou reprezentovány současně stejným segmentem, budou ortocentrum, středové barycentrum a circumcenter kolineární body, to znamená, že budou na stejné přímce:

Jak vypočítat obvod?

Obvod mnohoúhelníku se vypočítá sečtením stran.

Protože v tomto případě má rovnoramenný trojúhelník dvě strany se stejnou mírou, jeho obvod se počítá podle následujícího vzorce:

P = 2_*(strana a) + (strana b).

Jak vypočítat výšku?

Výška je čára kolmá k základně, rozděluje trojúhelník na dvě stejné části, když se rozprostírá na opačný vrchol.

Výška představuje protilehlou nohu (a), střed základny (b / 2) sousední nohu a strana „a“ představuje přeponu.

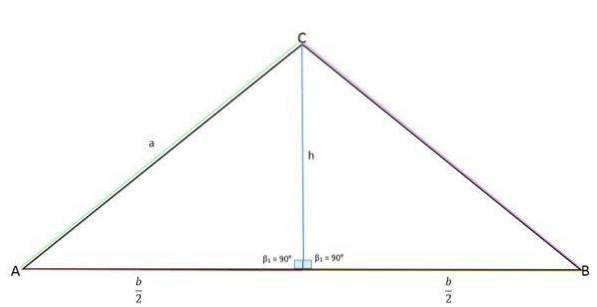
Pomocí Pythagorovy věty lze určit hodnotu výšky:

na^dva + b^dva = C^dva

Kde:

na^dva = výška (h).

b^dva = b / 2.

C^dva = strana a.

Dosazením těchto hodnot do Pythagorovy věty a řešením výšky máme:

h^dva + (b / dva)^dva = na^dva

h^dva + b^dva / 4 = na^dva

h^dva = na^dva - b^dva / 4

h = √ (na^dva - b^dva / 4).

Pokud je známý úhel tvořený shodnými stranami, lze výšku vypočítat pomocí následujícího vzorce:

Jak vypočítat plochu?

Plocha trojúhelníků se vždy počítá se stejným vzorcem, vynásobením základu krát výška a dělením dvěma:

Existují případy, kdy jsou známa pouze měření dvou stran trojúhelníku a úhel mezi nimi. V tomto případě je pro určení oblasti nutné použít trigonometrické poměry:

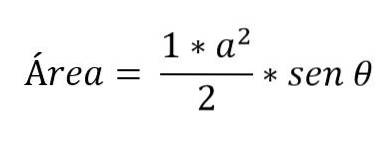
Jak vypočítat základ trojúhelníku?

Protože rovnoramenný trojúhelník má dvě stejné strany, je pro určení hodnoty jeho základny nutné znát alespoň míru výšky nebo jednoho z jeho úhlů.

Znát výšku se používá Pythagorova věta:

na^dva + b^dva = c^dva

Kde:

na^dva = výška (h).

C^dva = strana a.

b^dva = b / 2, není známo.

Řešíme pro b^dva vzorce a musíme:

b^dva = a^dva - C^dva

b = √ a^dva - C^dva

Jelikož tato hodnota odpovídá polovině základny, musí být vynásobena dvěma, aby se získala úplná míra základny rovnoramenného trojúhelníku:

b = 2 _* (√ a^dva - C^dva)

V případě, že je známa pouze hodnota jeho stejných stran a úhel mezi nimi, použije se trigonometrie, která nakreslí čáru od vrcholu k základně, která rozděluje rovnoramenný trojúhelník na dva pravé trojúhelníky.

Tímto způsobem se polovina základny počítá s:

Je také možné, že je známa pouze hodnota výšky a úhlu vrcholu, který je naproti základně. V takovém případě lze trigonometrií stanovit základ:

Výcvik

První cvičení

Najděte plochu rovnoramenného trojúhelníku ABC s vědomím, že dvě jeho strany jsou 10 cm a třetí strana je 12 cm.

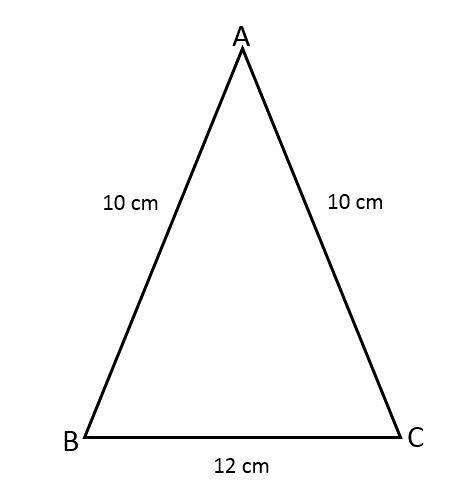
Řešení

Chcete-li najít oblast trojúhelníku, je nutné vypočítat výšku pomocí vzorce plochy, který souvisí s Pythagorovou větou, protože hodnota úhlu vytvořeného mezi stejnými stranami není známa.

Máme následující data rovnoramenného trojúhelníku:

• Stejné strany (a) = 10 cm.
• Základna (b) = 12 cm.

Hodnoty jsou ve vzorci nahrazeny:

Druhé cvičení

Délka dvou stejných stran rovnoramenného trojúhelníku je 42 cm, spojení těchto stran tvoří úhel 130^nebo. Určete hodnotu třetí strany, plochu trojúhelníku a obvod.

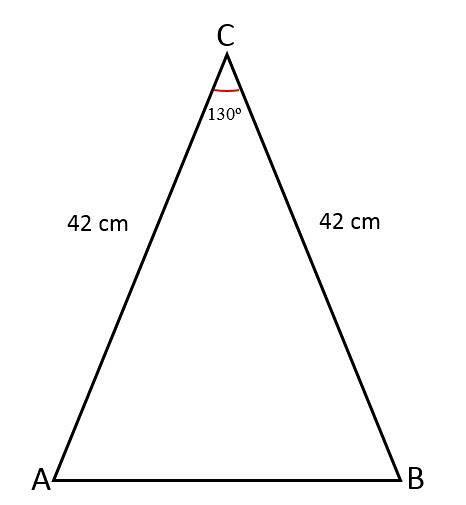
Řešení

V tomto případě jsou známa měření stran a úhel mezi nimi..

Chcete-li znát hodnotu chybějící strany, to znamená základnu tohoto trojúhelníku, nakreslí se na ni kolmá čára, která rozdělí úhel na dvě stejné části, jednu pro každý pravý trojúhelník, který je vytvořen.

• Stejné strany (a) = 42 cm.
• Úhel (Ɵ) = 130^nebo

Nyní trigonometrií se vypočítá hodnota poloviny základny, což odpovídá polovině přepony:

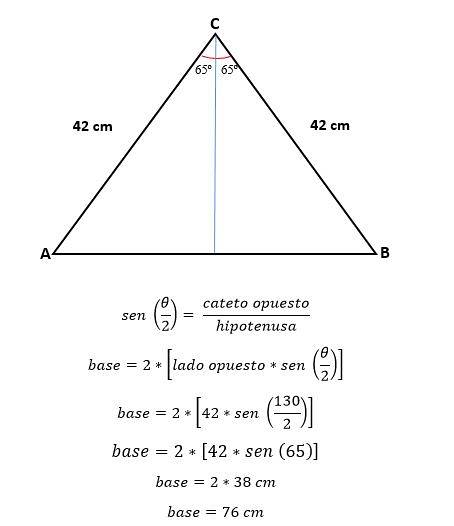
Pro výpočet plochy je nutné znát výšku trojúhelníku, kterou lze vypočítat pomocí trigonometrie nebo Pythagorovy věty, nyní již byla stanovena hodnota základny.

Podle trigonometrie to bude:

Vypočítá se obvod:

P = 2_*(strana a) + (strana b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Třetí cvičení

Vypočítejte vnitřní úhly rovnoramenného trojúhelníku s vědomím, že úhel základny je  = 55^nebo

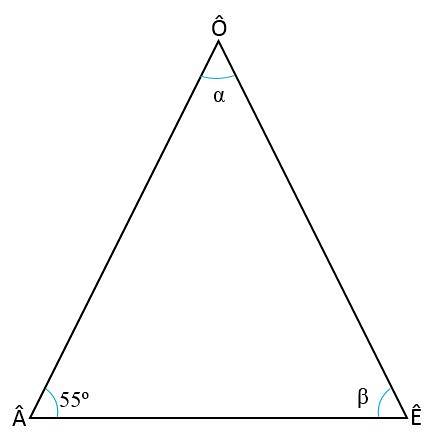
Řešení

Chcete-li najít dva chybějící úhly (Ê a Ô), je třeba si zapamatovat dvě vlastnosti trojúhelníků:

• Součet vnitřních úhlů každého trojúhelníku bude vždy = 180^nebo:

 + Ê + Ô = 180 ^nebo

• V rovnoramenném trojúhelníku jsou úhly základny vždy shodné, to znamená, že mají stejnou míru, proto:

 = Ô

Ê = 55^nebo

Abychom určili hodnotu úhlu Ê, dosadíme hodnoty ostatních úhlů do prvního pravidla a vyřešíme pro Ê:

55^nebo + 55^nebo + Ô = 180 ^nebo

110 ^nebo + Ô = 180 ^nebo

Ô = 180 ^nebo - 110 ^nebo

Ô = 70 ^nebo.

Reference

1. Álvarez, E. (2003). Prvky geometrie: s četnými cvičeními a geometrií kompasu. University of Medellin.
2. Álvaro Rendón, A. R. (2004). Technický výkres: kniha aktivit.
3. Angel, A. R. (2007). Elementární algebra. Pearson Education.
4. Arthur Goodman, L. H. (1996). Algebra a trigonometrie s analytickou geometrií. Pearson Education.
5. Baldor, A. (1941). Algebra. Havana: Kultura.
6. José Jiménez, L. J. (2006). Matematika 2.
7. Tuma, J. (1998). Příručka technické matematiky. Wolfram MathWorld.