
Pořadová proměnná


Co je pořadová proměnná?
Pořadová proměnná je proměnná, která přebírá hodnoty, které lze objednat (nebo označit objednávku). Například proměnnou výšku osoby lze rozdělit na: vysokou, průměrnou a krátkou.
Pořadová stupnice, kromě identifikace, seskupení a diferenciace studijních jednotek, jako nominální proměnné, popisuje také velikost, a proto se vyznačuje uspořádáním; to znamená, že studijní jednotky lze řadit ve vzestupném nebo sestupném pořadí, pokud jde o velikost.
V této stupnici mluvíme o první, druhé, třetí nebo vysoké, střední, nízké; ale mezi třídami není stanoveno žádné opatření. Například: proměnné hodnocení v testu spokojenosti s poskytovanou službou lze měřit ve čtyřech kategoriích: nespokojený, lhostejný, spokojený, velmi spokojený.
Lze jej objednat podle vyjádřené spokojenosti, ale není známo, jak odlišné je uspokojení od velmi spokojeného, ani není známo, zda je rozdíl mezi nespokojeným a lhostejným stejný jako mezi spokojeným a velmi spokojeným.
Pořadová stupnice odkazuje na měření, která porovnávají pouze „větší“, „menší“ nebo „stejná“ mezi po sobě jdoucími měřeními. Představuje klasifikaci nebo uspořádání sady pozorovaných hodnot.
Koncept a charakteristika běžné proměnné
Na ordinální stupnici jsou pozorování umístěna v relativním pořadí vzhledem k hodnocené charakteristice. To znamená, že kategorie dat jsou klasifikovány nebo seřazeny podle zvláštní charakteristiky, kterou mají.
Pokud použijeme čísla, jejich velikost představuje pořadí v hodnosti sledovaného atributu. Na pořadové stupnici měření mají význam pouze vztahy „větší než“, „menší než“ a „rovné“..
Z matematického hlediska a stejně jako nominální stupnice, řadové stupnice podporují pouze výpočet proporcí, procenta a poměrů.
Mírou centrální tendence, která nejlépe vysvětluje ordinální proměnnou, je medián, což je hodnota, která se nachází ve středu datové sady seřazené od nejnižší po nejvyšší.
Když jsou objekty klasifikovány podle charakteristiky, je možné zjistit, který objekt má více či méně charakteristiky ve srovnání s jiným; ale rozdíl nelze vyčíslit.
Například tři objekty, které byly objednány jako „první“, „druhý“ a „třetí“, s přihlédnutím k některé vlastnosti. Druhé místo se liší od prvního částkou, která se nemusí nutně rovnat částce, o kterou se liší od třetího místa.
Příklady řadových proměnných

Některé příklady řadových proměnných:
- Sociální třída (A - vysoká; B - střední vysoká; C - střední; D - nízká; E - velmi nízká).
- Kvalitativní známky školy (I - nedostatečné; A - přijatelné; B - dobré; S - vynikající; E - vynikající).
- Vojenské hodnosti (generál, plukovník, podplukovník, major, kapitán atd.).
- Stupeň vzdělání (základní, střední škola, profesionální technik, technolog, univerzita atd.).
- Fáze vývoje člověka (novorozenec, dítě, dítě, mladý, dospělý, starší člověk).
- Klasifikace filmu (A - Všichni veřejní; B - starší 12 let; C - starší 18 let; D - starší 21 let).
- Zrání ovoce (zelené, pintona, zralé, velmi zralé, shnilé).
- Míra spokojenosti s poskytováním veřejné služby. (Velmi spokojený; spokojený; lhostejný; atd.).
- Vysvětlení příkladů
Hodnocení učitele jeho studenty
Studenti určitého kurzu mají možnost vyplnit hodnotící průzkum pedagogické kapacity svého učitele, který se měří řadovou proměnnou, jejíž stupnice je: 5 - vynikající, 4 - dobrý, 3 - průměrný, 2 - špatný, 1 - Špatný.
Hodnoty proměnné jsou seřazeny od nejvyšší nebo nejlepší po nejnižší nebo nejhorší: vynikající je lepší než dobrý, dobrý je lepší než průměr atd. Nelze však rozlišit velikost rozdílů.
Je rozdíl mezi vynikajícím a dobrým stejný jako mezi špatným a špatným? Není možné potvrdit.
Použijeme-li čísla, neznamená to velikost. Například by nemělo dojít k závěru, že hodnocení Dobrý (hodnocení 4) je dvakrát vyšší než hodnocení Bad (hodnocení 2). Lze jen říci, že dobré hodnocení je lepší než špatné hodnocení, ale nelze ho vyčíslit, do jaké míry je lepší..
Úroveň přijetí jídla
Degustační soutěž hodnotí jídla v soutěži o vaření pomocí pořadové proměnné úrovně přijatelnosti vyjádřené v: A - vynikající, B - dobrá, C - nepřijatelná. Je prokázáno použití stupnice měření seřazené od nejvyšší po nejnižší, ale není možné stanovit rozdíl mezi hodnotami stupnice.
Jelikož se jedná o soutěž, jak se určuje vítěz? Zdá se, že nejvhodnější je použití módy k rozhodnutí o vítězi soutěže. Pochopte režim jako název pro nejvyšší hodnotu (nejčastější) z počtu na úrovni. Například bylo spočítáno 5 A, 14 B, 10 C; režim je B, protože to je úroveň, která měla nejvíce názorů.
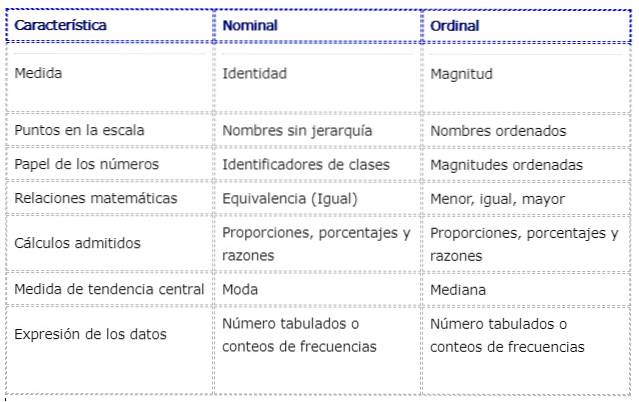
Rozdíly s nominální proměnnou
Následující tabulka ukazuje některé rozdíly a podobnosti mezi proměnnými měřenými ve jmenovité a pořadové stupnici:
Reference
- Freund, R.; Wilson, W.; Mohr, D. (2010). Statistické metody. Třetí ed. Academic Press-Elsevier Inc..
- Glass, G.; Stanley, J. (1996). Statistické metody neaplikované na sociální vědy. Prentice Hall Hispanoamericana S. A.
- Roztomilý.; Marchal, W .; Wathen, S. (2012). Statistiky aplikované na podnikání a ekonomiku. Patnácté vydání. McGraw-Hill / Interamericana Editores S. A.
- Orlandoni, G. (2010). Statistické měřicí stupnice. Časopis Telos. Obnoveno z ojs.urbe.edu.
- Siegel, S.; Castellan, N. (1998). Neparametrické statistiky aplikované na behaviorální vědy. Čtvrté vydání Redakční společnost Trillas S. A.
- Wikipedia. (2019). Úroveň měření. Obnoveno z en.wikipedia.org.



Zatím žádné komentáře