
Areolární rychlost, jak se počítá a řeší cvičení
The areolární rychlost je oblast zametaná za jednotku času a je konstantní. Je specifický pro každou planetu a vychází z popisu druhého Keplerova zákona v matematické formě. V tomto článku vysvětlíme, co to je a jak se počítá.
Boom, který představuje objev planet mimo sluneční soustavu, oživil zájem o planetární pohyb. Nic nenasvědčuje tomu, že by tyto exoplanety následovaly jiné zákony, než jaké jsou již známé a platné ve sluneční soustavě: Keplerovy zákony..
Johannes Kepler byl astronom, který bez pomoci dalekohledu a pomocí pozorování svého mentora Tycha Brahe vytvořil matematický model, který popisuje pohyb planet kolem Slunce..
Opustil tento model ztělesněný ve třech zákonech, které nesou jeho jméno a které dnes zůstávají stejně platné jako v roce 1609, kdy založil první dva, a v roce 1618, kdy vyhlášen třetí..
Rejstřík článků
- 1 Keplerovy zákony
- 2 Proč se planety pohybují elipticky kolem Slunce?
- 3 Velikost lineární rychlosti planety není konstantní
- 4 Areolární rychlost
- 5 Výpočet lineární rychlosti a areolární rychlosti
- 5.1 Cvičení
- 6 Bibliografie
Keplerovy zákony
V dnešní řeči zní Keplerovy tři zákony takto:
1. Oběžné dráhy všech planet jsou eliptické a Slunce je zaostřeno.
2. Polohový vektor ze Slunce na planetu zametá stejné oblasti ve stejném čase.
3. Čtverec orbitální periody planety je úměrný krychli popsané hlavní poloosy elipsy..
Planeta bude mít lineární rychlost, stejně jako jakýkoli známý pohybující se objekt. A je toho ještě víc: při psaní druhého Keplerova zákona v matematické formě vzniká nový koncept, který se nazývá areolární rychlost, typická pro každou planetu..
Proč se planety pohybují elipticky kolem Slunce?
Země a další planety se pohybují kolem Slunce díky tomu, že na ně působí silou: gravitační přitažlivostí. Totéž se děje s jakoukoli jinou hvězdou a planetami, které tvoří její systém, pokud je má..
Jedná se o sílu typu známého jako centrální síla. Hmotnost je ústřední silou, kterou každý zná. Objekt, který vyvíjí centrální sílu, ať už je to Slunce nebo vzdálená hvězda, přitahuje planety k jeho středu a pohybují se v uzavřené křivce.
V zásadě lze tuto křivku aproximovat jako obvod, stejně jako polský astronom Nicolás Copernicus, který vytvořil heliocentrickou teorii..
Odpovědnou silou je gravitační přitažlivost. Tato síla závisí přímo na hmotách hvězdy a planety a je nepřímo úměrná druhé mocnině vzdálenosti, která je odděluje..
Problém není tak snadný, protože ve sluneční soustavě všechny prvky interagují tímto způsobem a dodávají hmotě složitost. Navíc to nejsou částice, protože hvězdy a planety mají měřitelnou velikost..
Z tohoto důvodu není centrální bod oběžné dráhy nebo okruhu procházejícího planetami přesně vycentrován na hvězdě, ale v bodě známém jako těžiště systému sluneční planety..
Výsledná oběžná dráha je eliptická. Následující obrázek to ukazuje, přičemž příkladem je Země a Slunce:
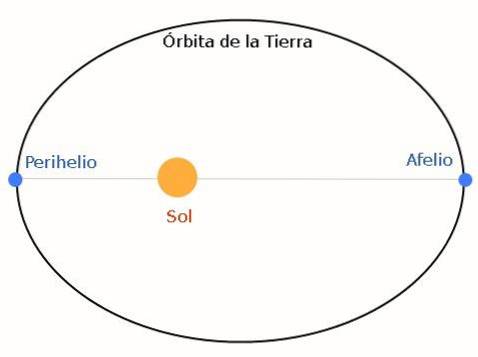
Aphelion je nejvzdálenější pozice na Zemi od Slunce, zatímco perihelion je nejbližší bod. Elipsa může být víceméně zploštělá, v závislosti na charakteristikách systému hvězdných planet..
Hodnoty aphelionu a perihelionu se každoročně mění, protože ostatní planety způsobují poruchy. U jiných planet se tyto pozice nazývají apoaster a periaster..
Velikost lineární rychlosti planety není konstantní
Kepler zjistil, že když planeta obíhá kolem Slunce, během svého pohybu zametá stejnou plochu ve stejný čas. Obrázek 2 graficky ukazuje význam tohoto:
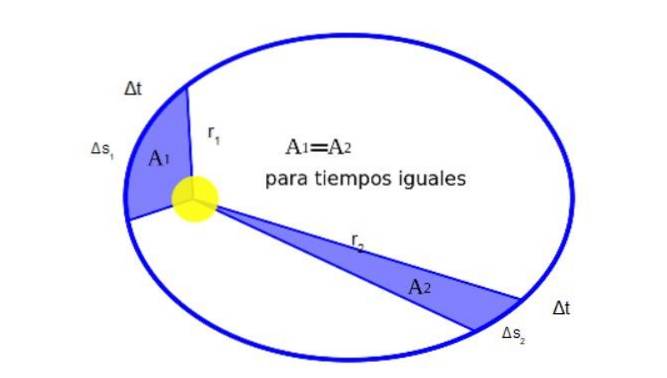
Matematicky skutečnost, že A1 být rovno Adva je vyjádřen takto:

Oblouky, které prošly Δs, jsou malé, takže každá oblast se může přibližně blížit trojúhelníku:
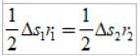
Protože Δs =protiΔt, kde v je lineární rychlost planety v daném bodě, dosazením máme:
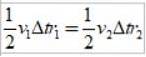
A protože časový interval Δt je stejný, získáme:
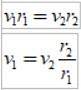
Jako rdva > r1, pak v1 > vdva, jinými slovy, lineární rychlost planety není konstantní. Ve skutečnosti jde Země rychleji, když je v perihéliu, než když je v aféliu..
Proto lineární rychlost Země nebo jakékoli planety kolem Slunce není velikost, která slouží k charakterizaci pohybu uvedené planety..
Areolární rychlost
Druhý Keplerův zákon naznačuje novou velikost zvanou areolární rychlost. Je definována jako plocha zametená za jednotku času a je konstantní. K jeho výpočtu se používá následující obrázek:
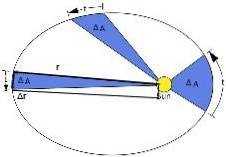
Vybírá se malá oblast zametená Zemí, přičemž se vytváří její eliptický obvod, který označíme jako ΔA. Čas potřebný k tomu je Δt.
Obrázek 3 ukazuje polohový vektor Země vzhledem ke Slunci, označený r. Když se Země pohybuje, zažívá posun Δr.
Tato oblast odpovídá polovině plochy obdélníku zobrazeného na obrázku 3:
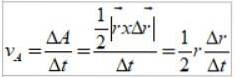
Kvocient Δr / Δt je přesně lineární rychlost Země, takže areolární rychlost je jako:
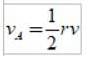
Jednotky vNA v mezinárodním systému jsou:
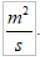
Všimněte si, že i když r i v se liší, produkt zůstává konstantní. Díky tomu je areolární rychlost velmi přiměřenou velikostí, aby charakterizovala pohyb planety kolem její hvězdy..
Produkt r a v je velikost momentu hybnosti L, takže areolární rychlost může být vyjádřena jako:
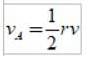
Výpočet lineární rychlosti a areolární rychlosti
V následujícím příkladu si ukážeme, jak vypočítat areolární rychlost, když jsou známy některé parametry planetárního pohybu:
Cvičení
Exo-planeta se pohybuje kolem svého slunce po eliptické dráze, podle Keplerových zákonů. Když je v periasteru, jeho poloměr vektor je r1 = 4 107 km, a když je v apoastru, je to rdva = 15 107 km. Lineární rychlost na jeho periasteru je v1 = 1000 km / s.
Vypočítat:
A) Velikost rychlosti v apoastru.
B) Areolární rychlost exoplanety.
C) Délka hlavní poloosy elipsy.
Odpovědět)
Používá se rovnice:
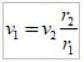
ve kterém jsou nahrazeny číselné hodnoty.
Každý termín je identifikován následovně:
proti1 = rychlost v apoastru; protidva = rychlost v periasteru; r1= vzdálenost od apoastra,
rdva= vzdálenost od periastera.
S těmito hodnotami získáte:

Odpověď B)
Rovnice, která se má použít, je
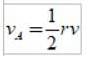
ve kterém lze nahradit dvojici hodnot r a v periasteru nebo apoasteru, protože vNA je konstanta planety:

Odpověď C)
Délka hlavní poloosy elipsy je semisem apoastra a periasteru:
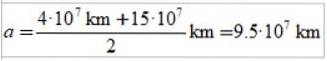
Bibliografie
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 1. Mexiko. Cengage Learning Editors. 367-372.
- Stern, D. (2005). Keplerovy tři zákony planetárního pohybu. Obnoveno z pwg.gsfc.nasa.gov
- Poznámka: navrhované cvičení bylo převzato a upraveno z následujícího textu v knize McGrawHill. Bohužel se jedná o izolovanou kapitolu ve formátu pdf, bez názvu nebo autora: mheducation.es/bcv/guide/capitulo/844817027X.pdf


Zatím žádné komentáře